组合数学中那些有趣的球和盒子的问题(超强闷骚版,再也不怕球球了)
介绍一下问题:
n个球放到m个盒子里,则球和盒子是否有区别?是否允许空盒?
这自然有23=8种状态,用表格表示方案情况如下:
第一种情况的解释:(n个无区别的球放进m个无区别的盒子中,允许空盒)
第二种情况的解释:(n个无区别的球放进m个无区别的盒子中,不允许空盒)
将这两种情况放在一起,这是因为这是同一个问题:正整数的拆分问题。所谓正整数的拆分问题指的是指把一个正整数拆分成若干正整数的和。不同的拆分法的数目称为拆分数。
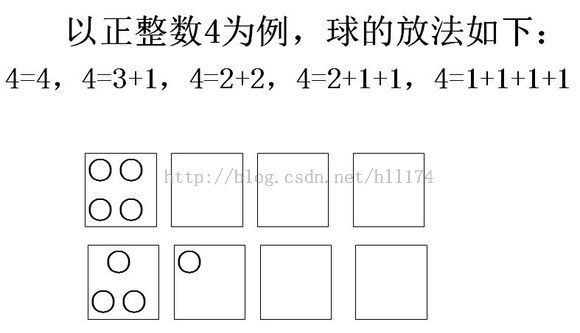
例如:考虑正整数4的拆分数:
4=4,4=3+1,4=2+2,4=2+1+1,4=1+1+1+1
正整数n的拆分,相当于把n个无区别的球放进m个无区别的盒子,盒子中允许放一个以上的球,也允许空着。依然以上面的4的拆分数为例子来说明:
上边对应着4=4和4=3+1的两种情况,其他的也类似,现在你已经同意这个观点了“正整数n的拆分,相当于把n个无区别的球放进m个无区别的盒子,盒子中允许放一个以上的球,也允许空着。”好记住了它吧,凡是球无区别,盒子无区别,这一定是整数拆分问题。当然通过上面举得例子你也会发现m>=n,毕竟最终有全是1的和的形式。
好了,有了上述我们达成的共识,下面我们继续没有完成的任务。
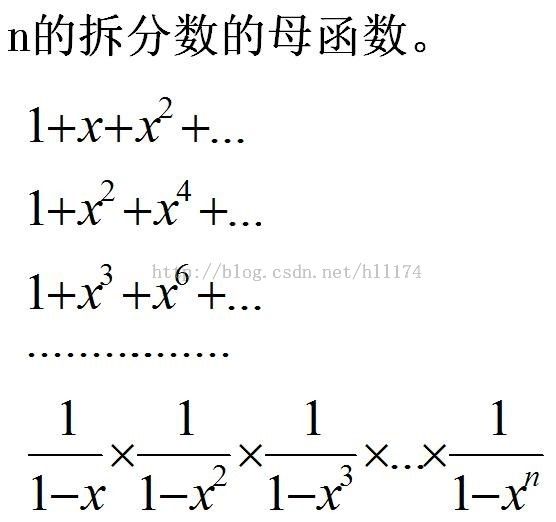
注:xn表示x的n次方,以下不再解释。
上述公式中第一行是什么意思呢,就是“1”表示拆分数中有0个1,“x”表示有1个1,“x2”表示有2个1,依此类推....
第二行什么意思呢,就是“1”表示拆分数中有0个2,“x2”表示有1个2,“x4”表示有2个2,一次类推....
我相信第三行以及以下你一定知道什么意思了。
通过无穷级数你肯定能得出最后一行的形式的,说白了就是一个无穷等比数列求和。最后一行中x的n次方的系数,就是我们要求的结果。有这么神奇么,还是用4的拆分数来验证一下吧,自己算算x4的系数吧。

很神奇吧,好了言归正传吧。“n个无区别的球放进m个无区别的盒子中,(是否)允许空盒。”自然要用上面的理论来解决了。这里我相信你能得出表格中我写的原因解释了。
我们继续,看看第三种和第四种情况。
“n个无区别的球,放入m个有区别的盒子中,(是否)允许为空。”
我觉得原因解释解释的很清楚了,你需要的就是记住下面的公式:
公式怎么推出来的,其实你学过的,给你个提示奥,去看看幂级数吧,再说的明白一点就是(1-x)分之一不断的求导。
我们继续看看5,6种情况。
“n个有区别的球,放入m个无区别的盒子中,(是否)允许为空。”

也就是表格中我用红色标注的那两行。
“n个有区别的球,放入m个无区别的盒子中,(是否)允许为空。”这个问题一定是允许重复的排列问题,也就是指数型母函数问题。
对原因解析中的内容做更加详细的解释;
“n个不同的元素,取m个作有重复的排列,与m个不同的球放进n个有区别的盒子,允许空盒的放法一一对应.”
上述这个例子,便可以说明问题了。所以看我写的原因注释吧,我相信你明白了。
终于,剩下两种情况了,我们马上就要解放了,好,加油了。

先来看看第二类斯特林数的定义:
“n个有区别的球放到m个相同的盒子中,要求无一空盒,其不同的方案数用S(n,m)表示,称为第二类司特林数。”
“n个有区别的球,放入m个无区别的盒子中”,我们把盒子做一下全排列,会是什么情况呢,你不觉得就是m个不同的盒子了么。也就是“n个有区别的球,放入m个有区别的盒子中”的情况了么?我假设你同意了,那S(n,m)怎么求你也就会了,不是么?哈哈,好好看看我写的原因解释吧。这里不再罗嗦了。
最后我觉得我解决了所有的问题,现在写的东西怎么这种感觉呢。哎,怪就怪最近看Meyers的书看的吧,语气就是跟他学的,你看这篇文章的时候没有感觉到我再跟你对话么?如果有,恭喜你,你已经掌握了。