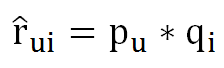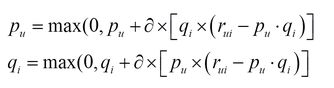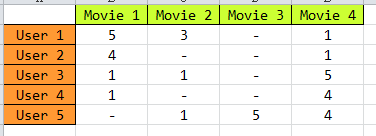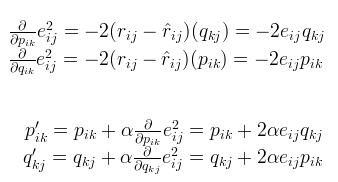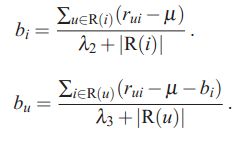***基于协同过滤,NMF和Baseline的推荐算法
目录[-]
杂谈
老早就想整理一篇推荐算法的入门博文,今天抽空写一下。本文以电影推荐系统为例,简单地介绍基于协同过滤,PMF概率矩阵分解,NMF非负矩阵分解和Baseline的推荐系统算法。NMF的实现具体可以参考Reference中的「基于矩阵分解的推荐算法,简单入门」一文,对我启发很大。
基于协同过滤的推荐算法
什么是协同过滤?协同过滤是利用集体智慧的一个典型方法。要理解什么是协同过滤 (Collaborative Filtering, 简称 CF),首先想一个简单的问题,如果你现在想看个电影,但你不知道具体看哪部,你会怎么做?大部分的人会问问周围的朋友,看看最近有什么好看的电影推荐,而我们一般更倾向于从口味比较类似的朋友那里得到推荐;或者,搜索与你喜欢的电影同类型的电影推荐。
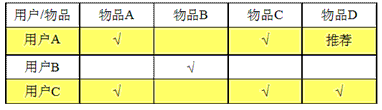
User-based的推荐算法
如上图,我们收集到用户-电影评价矩阵,假设用户A对于物品D的评价为null,这时我们对比用户A、用户B、用户C的特征向量(以物品评价为特征),可以发现用户A与用户C的相似度较大,这时我们可以认为,对于用户C喜欢的物品D,用户A也应该喜欢它,这是就把物品D推荐给用户A。
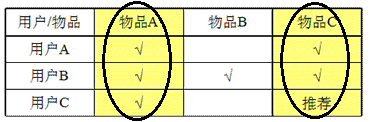
Item-based的推荐算法
同理,我们对比物品A、物品B、物品C的特征向量(以用户对该物品的喜欢程度为特征),发现物品A与物品C很像,就把用品C推荐给喜欢物品A的用户C。
SVD和PMF概率矩阵分解
在实际业务场景中,user-Item矩阵有可能非常稀疏,存储率有可能连1%都达不到。怎么办呢?通常使用矩阵分解算法来提取出更有用的信息。SVD在矩阵分解方面可以参考基于SVD实现PCA的图像识别 一文,把它分解成用户矩阵(左奇异特征向量矩阵)和物品矩阵(右奇异特征向量矩阵)分别代表各自的特性。
但是SVD算法的时间复杂度很大,不适合用来解决这种比数据量较大的问题,这时就有PMF概率矩阵分解。把用户-电影 评分看成一个矩阵,rui表示u对电影i的评分,于是电影评分矩阵可以这样来估计:
其中P和Q就相当于SVD中的前k 个特征向量构成的矩阵,分别描述user-based和item-based。在PMF中使用SGD(随机梯度下降)进行优化时,使用如下的迭代公式:
我们把证明放到下一章节 NMF非负矩阵分解,NMF其实就是在PMF的基础上加入一点约束,具体约束公式如下:
基于NMF非负矩阵分解的推荐算法
我们知道,要做推荐系统,最基本的一个数据就是,用户-物品的评分矩阵,如下图所示:
矩阵中,描述了5个用户(U1,U2,U3,U4 ,U5)对4个物品(D1,D2,D3,D4)的评分(1-5分),“-” 表示没有评分,现在目的是把没有评分的 给预测出来,然后按预测的分数高低,给用户进行推荐。
如何预测缺失的评分呢?对于缺失的评分,可以转化为基于机器学习的回归问题,也就是连续值的预测,对于矩阵分解有如下式子,R是类似图的评分矩阵,假设N*M维(N表示行数,M表示列数),可以分解为P跟Q矩阵,其中P矩阵维度N*K,P矩阵维度K*M。
对于P,Q矩阵的解释,直观上,P矩阵是N个用户对K个主题的关系,Q矩阵是K个主题跟M个物品的关系,至于K个主题具体是什么,在算法里面K是一个参数,需要调节的,通常10~100之间。
对于上式的左边项,表示的是R^ 第i 行,第j 列的元素值,对于如何衡量矩阵分解的好坏,我们给出如下风险函数:
有了风险函数,我们就可以采用梯度下降法不断地减小损失值,直到不能再减小为止,最后的目标,就是每一个元素(非缺失值)的e(i,j)的总和 最小。我们可以得到如下梯度以及p、q的更新方式(其中α是学习步长,详见李航《统计机器学习》):
在训练p、q参数过程中,为了防止过拟合,我们给出一个正则项,风险函数修改如下:
相应的p、q参数学习更新方式如下:
至此,我们就可以学习出p、q矩阵,将p x q就可以得到新的估计矩阵,由于加入了非负处理(缺失值部分的处理),我们可以发现原先缺失的地方有了一个估计值,这个估计值就作为了推荐的分值(其实就是拿非缺失值部分作参数学习训练,学习出来的结果当然不会有负数)。NMF实现代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
|
package
nmf;
public
class
Nmf {
public
double
[][] RM, PM, QM;
public
int
Kc, Uc, Oc;
public
int
steps;
public
double
Alpha, Beta;
public
void
run() {
for
(
int
s =
0
; s < steps; s++) {
// 梯度下降更新
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Oc; j++) {
if
(RM[i][j] >
0
) {
// 计算eij
double
e =
0
, pq =
0
;
for
(
int
k =
0
; k < Kc; k++) {
pq += PM[i][k] * QM[k][j];
}
e = RM[i][j] - pq;
// 更新Pik和Qkj,同时保证非负
for
(
int
k =
0
; k < Kc; k++) {
PM[i][k] += Alpha
* (
2
* e * QM[k][j] - Beta * PM[i][k]);
// PM[i][k] = PM[i][k] > 0 ? PM[i][k] : 0;
QM[k][j] += Alpha
* (
2
* e * PM[i][k] - Beta * QM[k][j]);
// QM[k][j] = QM[k][j] > 0 ? QM[k][j] : 0;
}
}
}
}
// 计算风险损失
double
loss =
0
;
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Oc; j++) {
if
(RM[i][j] >
0
) {
// 计算eij^2
double
e2 =
0
, pq =
0
;
for
(
int
k =
0
; k < Kc; k++) {
pq += PM[i][k] * QM[k][j];
}
e2 = Math.pow(RM[i][j] - pq,
2
);
for
(
int
k =
0
; k < Kc; k++) {
e2 += Beta
/
2
* (Math.pow(PM[i][k],
2
) + Math.pow(
QM[k][j],
2
));
}
loss += e2;
}
}
}
if
(loss <
0.01
) {
System.out.println(
"OK"
);
break
;
}
// if (s % 100 == 0) {
// System.out.println(loss);
// }
}
}
public
Nmf(
double
[][] RM,
double
[][] PM,
double
[][] QM,
int
Kc,
int
Uc,
int
Oc,
int
steps,
double
Alpha,
double
Beta) {
this
.RM = RM;
this
.PM = PM;
this
.QM = QM;
this
.Kc = Kc;
this
.Uc = Uc;
this
.Oc = Oc;
this
.steps = steps;
this
.Alpha = Alpha;
this
.Beta = Beta;
}
}
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
package
nmf;
import
java.util.Scanner;
public
class
Keyven {
public
static
void
main(String[] args) {
int
Uc =
5
, Oc =
4
, Kc =
2
;
double
[][] RM =
new
double
[Uc][Oc];
double
[][] PM =
new
double
[Uc][Kc];
double
[][] QM =
new
double
[Kc][Oc];
/*
* 5 3 0 1 4 0 0 1 1 1 0 5 1 0 0 4 0 1 5 4
*/
Scanner input =
new
Scanner(System.in);
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Oc; j++) {
RM[i][j] = input.nextDouble();
}
}
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Oc; j++) {
System.out.printf(
"%.2f\t"
, RM[i][j]);
}
System.out.println();
}
System.out.println();
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Kc; j++) {
PM[i][j] = Math.random() %
9
;
}
}
for
(
int
i =
0
; i < Kc; i++) {
for
(
int
j =
0
; j < Oc; j++) {
QM[i][j] = Math.random() %
9
;
}
}
// 最多迭代5000次,学习步长控制为0.002,正则项参数设置为0.02
Nmf nmf =
new
Nmf(RM, PM, QM, Kc, Uc, Oc,
5000
,
0.002
,
0.02
);
nmf.run();
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Oc; j++) {
double
temp =
0
;
for
(
int
k =
0
; k < Kc; k++) {
temp += PM[i][k] * QM[k][j];
}
System.out.printf(
"%.2f\t"
, temp);
}
System.out.println();
}
input.close();
}
}
|
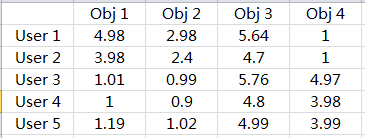
实验结果:
基于Baseline的推荐算法
要评估一个策略的好坏,就需要建立一个对比基线,以便后续观察算法效果的提升。此处我们可以简单地对推荐算法进行建模作为基线。假设我们的训练数据为: <user, item, rating>三元组, 其中user为用户id, item为物品id(item可以是MovieLens上的电影,Amazon上的书, 或是百度关键词工具上的关键词), rating为user对item的投票分数, 其中用户u对物品i的真实投票分数我们记为rui,基线(baseline)模型预估分数为bui,则可建模如下:
其中mu(希腊字母mu)为所有已知投票数据中投票的均值,bu为用户的打分相对于平均值的偏差(如果某用户比较苛刻,打分都相对偏低, 则bu会为负值;相反,如果某用户经常对很多片都打正分, 则bu为正值); bi为该item被打分时,相对于平均值得偏差,可反映电影受欢迎程度。 bui则为基线模型对用户u给物品i打分的预估值。该模型虽然简单, 但其中其实已经包含了用户个性化和item的个性化信息, 而且特别简单(很多时候, 简单就是一个非常大的特点, 特别是面对大规模数据时)。
基线模型中, mu可以直接统计得到,我们的优化函数可以写为(其实就是最小二乘法):
也可以直接写成如下式子,因为它本身就是经验似然:
上述式子中u∈R(i) 表示评价过电影 i 的所有用户,|R(i)| 为其集合的个数;同理,i∈R(u) 表示用户 u 评价过的所有电影,|R(u)| 为其集合的个数。实现代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
package
baseline;
public
class
Baseline {
public
double
[] bi, bu;
public
double
[][] RM;
public
int
Uc, Ic;
public
double
lamada2, lamada3;
public
Baseline(
double
[][] RM,
int
Uc,
int
Ic,
double
lamada2,
double
lamada3) {
this
.RM = RM;
this
.lamada2 = lamada2;
this
.lamada3 = lamada3;
this
.Uc = Uc;
this
.Ic = Ic;
this
.bu =
new
double
[Uc];
this
.bi =
new
double
[Ic];
}
public
void
run() {
// 计算μ
double
avg =
0
;
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Ic; j++) {
avg += RM[i][j];
}
}
avg = avg / Uc / Ic;
// 更新bi
for
(
int
i =
0
; i < Ic; i++) {
double
bis =
0
;
int
Icnt =
0
;
// 点评过电影i的所有User个数
for
(
int
tu =
0
; tu < Uc; tu++) {
if
(RM[tu][i] !=
0
) {
bis += RM[tu][i] - avg;
Icnt++;
}
}
bi[i] = bis / ((
double
)Icnt + lamada2);
}
// 更新bu
for
(
int
u =
0
; u < Uc; u++) {
double
bus =
0
;
int
Ucnt =
0
;
// 用户u点评过得电影Item个数
for
(
int
ti =
0
; ti < Ic; ti++) {
if
(RM[u][ti] !=
0
) {
bus += RM[u][ti] - avg - bi[ti];
Ucnt++;
}
}
bu[u] = bus / ((
double
)Ucnt + lamada3);
}
for
(
int
u =
0
; u < Uc; u++) {
for
(
int
i =
0
; i < Ic; i++) {
if
(RM[u][i] ==
0
) {
RM[u][i] = avg + bi[i] + bu[u];
}
}
}
}
}
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
package
baseline;
import
java.util.Scanner;
public
class
Keyven {
public
static
void
main(String[] args) {
int
Uc =
5
, Ic =
4
;
double
[][] RM =
new
double
[Uc][Ic];
/*
* 5 3 0 1 4 0 0 1 1 1 0 5 1 0 0 4 0 1 5 4
*/
Scanner input =
new
Scanner(System.in);
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Ic; j++) {
RM[i][j] = input.nextDouble();
}
}
Baseline bl =
new
Baseline(RM, Uc, Ic,
0
,
0
);
bl.run();
for
(
int
i =
0
; i < Uc; i++) {
for
(
int
j =
0
; j < Ic; j++) {
System.out.printf(
"%.2f\t"
, RM[i][j]);
}
System.out.println();
}
input.close();
}
}
|
Baseline基线模型与NMF矩阵分解模型试验效果对比如下:
后记
什么是梯度下降?考虑下图一种简单的情形,风险函数为loss = kx,则总体损失就是积分∫kx dx,取梯度的反方向进行逐步更新至总体损失减小… …在我看来,其实,数据挖掘 = ①线性代数+②应用概率统计+③高数(积分、梯度等数理意义)+④李航《统计机器学习》神书+⑤算法与数据结构… …只要好好努力打好基础,人就能不断向前走下去^_^
Reference
从item-base到svd再到rbm,多种Collaborative Filtering(协同过滤算法)从原理到实现
百度电影推荐系统比赛 小结 ——记我的初步推荐算法实践
白话NMF(Non-negative Matrix Factorization)
基于矩阵分解的推荐算法,简单入门(证明算法,非常有用!)
SVD因式分解实现协同过滤-及源码实现
探索推荐引擎内部的秘密,第 2 部分: 深入推荐引擎相关算法 - 协同过滤
推荐系统中近邻算法与矩阵分解算法效果的比较——基于movielens数据集