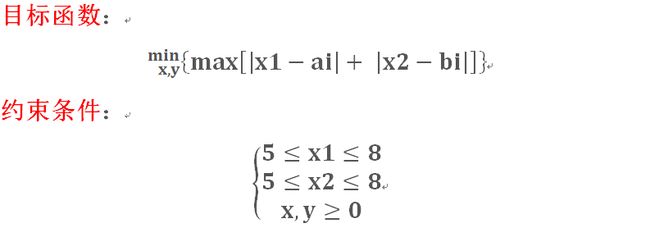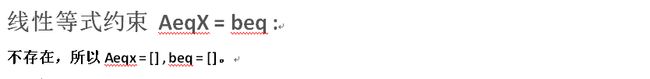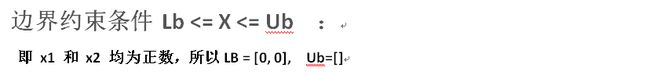MATLAB求多目标优化问题——fminimax

一、 fminimax函数 求解的模型 

minmax { f1, f2, f3, ……, f3}

s.t.  AX <= b (线性不等式约束)

         AeqX = beq (线性等式约束)

         C(X) <= 0 (非线性不等式约束条件)

         Ceq(X) = 0 (非线性等式约束)

         Lb <= X <= Ub (边界约束条件)

 

二、 fminimax函数用法说明

1. 调用格式  

x = fminimax(fun,x0)

x = fminimax(fun,x0,A,b)

x = fminimax(fun,x0,A,b,Aeq,beq)

x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub)（最常用的）

x =fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)

x =fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

[x,fval,maxfval] =fminimax(…)

[x,fval,maxfval,exitflag]= fminimax(…)

[x,fval,maxfval,exitflag,output]= fminimax(…)

[x,fval,maxfval,exitflag,output,lambda]= fminimax(…)

2. 参数说明

（1）fun为目标函数；

（2）x0为初始值；

（3）A、b满足线性不等约束 ，若没有不等约束，则取A=[ ]，b=[ ]；

（4）Aeq、beq满足等式约束 ，若没有，则取Aeq=[ ]，beq=[ ]；

（5）lb、ub满足 ，若没有界，可设lb=[ ]，ub=[ ]；

（6）nonlcon的作用是通过接受的向量x来计算非线性不等约束 和等式约束分别在x处的值C和Ceq，通过指定函数柄来使用，如：

>>x =fminimax(@myfun,x0,A,b,Aeq,beq,lb,ub,@mycon)，先建立非线性约束函数，并保存为mycon.m：function[C,Ceq] = mycon(x)

C = …    % 计算x处的非线性不等约束 的函数值。

Ceq = …   % 计算x处的非线性等式约束 的函数值。

（7）options为指定的优化参数；

（8）fval为最优点处的目标函数值；

（9）maxfval为目标函数在x处的最大值；

（10）exitflag为终止迭代的条件；

（11）lambda是Lagrange乘子，它体现哪一个约束有效。

（12）output输出优化信息。

 

三、 实例

设某城市有某种物品的10个需求点，第i个需求点Pi的坐标为(ai,bi),道路网与坐标轴平行，彼此正交。现打算建一个该物品的供应中心，且由于受到城市某些条件的限制，该供应中心只能设在x界于[5,8]，y界于[5.8]的范围之内。问该中心应建在何处为好?

P点的坐标为：

1. 题目分析

设供应中心的位置为(x,y)，要求它到最远需求点的距离尽可能小，则数学模型为：

 

 

2. fminimax函数参数分析

3. MATLAB代码

(1)主函数文件

%求解极大值的极小值的主函数 main.m:
clear;
clc;
 
%x初始值,随意设定
x0=[6;6];
 
%线性不等式约束AX <= b
A=[-10;1 0;0 -1;0 1];
b=[-5;8;-5;8];
 
%线性等式约束AeqX = beq
Aeq=[];
Beq= [];
 
%边界约束条件Lb <= X <= Ub
lb=[0;0];
ub=[];
 
[x,fva,maxfval,exitflag,output]=fminimax(@myfun,x0,A,b,Aeq, Beq,lb,ub)
plot(x(1),x(2),'bo')  % 图中标出要求的点

(2)目标函数文件

%目标函数文件 myfun.m:
functionf=myfun(x)
x1=[14 3 5 9 12 6 20 17 8];
x2=[210 8 18 1 4 5 10 8 9];
str=[repmat('(', 10, 1)  num2str(x1')  num2str(x2') repmat(  ')', 10, 1) ];
 
plot(x1,x2,'*r');%画出10个需求点
text(x1,x2,cellstr(str));     %给10个需求点标出坐标
hold on;
 
%返回10个需求点的各自的目标函数
fori=1:10
    f(i)=abs(x(1)-x1(i))+abs(x(2)-x2(i));
end