acdream oj 1211

Reactor Cooling

Special Judge  Time Limit: 2000/1000MS (Java/Others)  Memory Limit: 128000/64000KB (Java/Others)

Submit  Statistic  Next Problem

Problem Description

      The terrorist group leaded by a well known international terrorist Ben Bladen is buliding a nuclear reactor to produce plutonium for the nuclear bomb they are planning to create. Being the wicked computer genius of this group, you are responsible for developing the cooling system for the reactor.
      The cooling system of the reactor consists of the number of pipes that special cooling liquid flows by. Pipes are connected at special points, called nodes, each pipe has the starting node and the end point. The liquid must flow by the pipe from its start point to its end point and not in the opposite direction.
      Let the nodes be numbered from 1 to N . The cooling system must be designed so that the liquid is circulating by the pipes and the amount of the liquid coming to each node (in the unit of time) is equal to the amount of liquid leaving the node. That is, if we designate the amount of liquid going by the pipe from i-th node to j -th as fi,j, (put fi,j = 0 if there is no pipe from node i to node j ), for each i the following condition must hold:

      Each pipe has some finite capacity, therefore for each i and j connected by the pipe must be fi,j ≤ ci,j where ci,j is the capacity of the pipe. To provide sufficient cooling, the amount of the liquid flowing by the pipe going from i-th to j -th nodes must be at least li,j , thus it must be fi,j ≥ li,j. Given ci,j and li,j for all pipes, find the amount fi,j, satisfying the conditions specified above

Input

      The first line of the input file contains the number N (1 ≤ N ≤ 200) - the number of nodes and and M — the number of pipes. The following M lines contain four integer number each - i, j , l i,j and c i,j each. There is at most one pipe connecting any two nodes and 0 ≤ l i,j ≤ c i,j ≤ 10 5 for all pipes. No pipe connects a node to itself. If there is a pipe from i-th node to j -th, there is no pipe from j -th node to i-th.

Output

      On the first line of the output file print YES if there is the way to carry out reactor cooling and NO if there is none. In the first case M integers must follow, k-th number being the amount of liquid flowing by the k-th pipe. Pipes are numbered as they are given in the input file.

Sample Input

4 6
1 2 1 2
2 3 1 2
3 4 1 2
4 1 1 2
1 3 1 2
4 2 1 2
4 6
1 2 1 3
2 3 1 3
3 4 1 3
4 1 1 3
1 3 1 3
4 2 1 3

Sample Output

NO
YES
1
2
3
2
1
1
分类：无源无汇的有上下界网络流。

题意：
   给n个点，及m根pipe，每根pipe用来流躺液体的，单向的，每时每刻每根pipe流进来的物质要等于流出去的物质，要使得m条pipe组成一个循环体，里面流躺物质。
并且满足每根pipe一定的流量限制，范围为[Li,Ri].即要满足每时刻流进来的不能超过Ri(最大流问题)，同时最小不能低于Li。
输出每根pipe里的流量
例如：
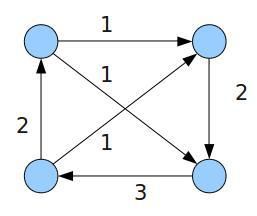
4 6(4个点，6个pipe) 1 2 1 3 (1->2上界为3，下界为1) 2 3 1 3 3 4 1 3 4 1 1 3 1 3 1 3 4 2 1 3
可行流：
 

再如：所有pipe的上界为2下界为1的话，就不能得到一种可行流。
 
题解：
上界用ci表示，下界用bi表示。
下界是必须流满的，那么对于每一条边，去掉下界后，其自由流为ci– bi。
主要思想：每一个点流进来的流=流出去的流
对于每一个点i，令
Mi= sum(i点所有流进来的下界流)– sum(i点所有流出去的下界流)
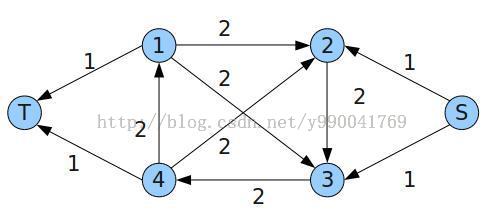
如果Mi大于0，代表此点必须还要流出去Mi的自由流，那么我们从源点连一条Mi的边到该点。
如果Mi小于0，代表此点必须还要流进来Mi的自由流，那么我们从该点连一条Mi的边到汇点。
如果求S->T的最大流，看是否满流(S的相邻边都流满)。
满流则有解，否则无解。
 

 
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdio.h>
#include <vector>
using namespace std;
const int maxn=100110,maxm=400100;
int n,m;
struct Edge
{
    int to,cap,next;
} edge[maxm ];
int tot,head[maxn];

void init(int n)
{
    tot=0;
    memset(head,-1,sizeof(head));
}

void add_edge(int u,int v,int cap)
{
    edge[tot].to=v;
    edge[tot].cap=cap;
    edge[tot].next=head[u];
    head[u]=tot++;


    edge[tot].to=u;
    edge[tot].cap=0;
    edge[tot].next=head[v];
    head[v]=tot++;
}
int dis[maxn],cur[maxn],gap[maxn],pre[maxn];
int flow[500][500];
int sap(int S,int T,int num)
{
    memset(dis,0,sizeof(dis));
    memset(gap,0,sizeof(gap));
    memcpy(cur,head,sizeof(head));
    int u=pre[S]=S;
    int maxflow=0,aug=-1;
    gap[0]=num;
    while(dis[S]<num)
    {
loop:
        for(int &i=cur[u]; i!=-1; i=edge[i].next)
        {
            int v=edge[i].to;
            if(edge[i].cap&&dis[u]==dis[v]+1)
            {
                if(aug==-1||aug>edge[i].cap)
                    aug=edge[i].cap;
                pre[v]=u;
                u=v;
                if(v==T)
                {
                    maxflow+=aug;
                    for(u=pre[u]; v!=S; v=u,u=pre[u])
                    {
                        edge[cur[u]].cap-=aug;
                        edge[cur[u]^1].cap+=aug;
                        int gv=edge[cur[u]].to;
                        flow[u][gv]+=aug;
                        ///+++
                    }
                    aug=-1;
                }
                goto loop;
            }
        }
        int mindis=num;
        for(int i=head[u]; i!=-1; i=edge[i].next)
        {
            int v=edge[i].to;
            if(edge[i].cap&&mindis>dis[v])
            {
                cur[u]=i;
                mindis=dis[v];
            }
        }
        if((--gap[dis[u]])==0)
            break;
        gap[ dis[u]=mindis+1 ]++;
        u=pre[u];
    }
    return maxflow;
}

struct point
{
    int xb,wi;
    point(){;}
    point(int a,int b)
    {
        xb=a,wi=b;
    }
};
vector<point>ff;
int come[maxn],in[maxn];
int main()
{
    int S,T;
    while(scanf("%d%d",&n,&m)!=-1)
    {
        init(n);
        memset(flow,0,sizeof(flow));
        memset(in,0,sizeof(in));
        memset(come,0,sizeof(come));
        for(int i=0; i<m; i++)
        {
            int u,v,mi,ma;
            scanf("%d%d%d%d",&u,&v,&mi,&ma);

            add_edge(u,v,ma-mi);
            ff.push_back(point(tot-1,mi));

            come[u]+=mi;
            in[v]+=mi;
        }
        S=0,T=n+1;
        int Flow=0;
        for(int i=1; i<=n; i++)
        {
            int temp=come[i]-in[i];
            if(temp<0)
            {
                 Flow-=temp;
            add_edge(S,i,-temp);
            }

            if(temp>0)
                add_edge(i,T,temp);

        }
        int ans=sap(S,T,n+2);
        if(ans==Flow)
        {
            printf("YES\n");
            for(int i=0;i<ff.size();i++)
            {
                int v=ff[i].xb;
                printf("%d\n",edge[v].cap+ff[i].wi);
            }
        }
        else
            printf("NO\n");
            for(int i=0;i<=n+3;i++)
                ff.clear();
    }
}