Yale开放课程博弈论19
19. 招商引资和战略投资
上一讲我们讲了太多概念,今天主要讲三个案例。
案例一
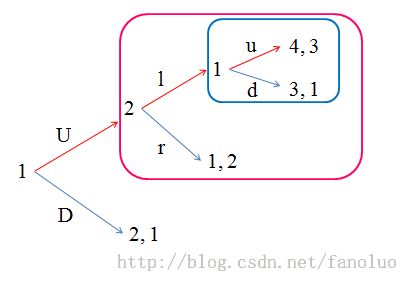
把全班同学分成两组进行游戏,大部分同学的选择趋向于[U, l, u]。
逆向归纳法分析:参与者1有第二次选择的机会的话,会选择u,因为4(选择u)比3(选择d)好。对于参与者2,如果他选择r的话游戏结束,其收益为2,而他根据逆向归纳法他知道若自己选择l的话参与者1肯定会选择u,那时自己的收益是3,所以他会选择l。再接着逆推到参与者1的第一次选择,他会选择U,因为根据逆向归纳法他知道自己选择U之后参与者会选择l,自己会再选择u,收益为4,比直接选择D的收益2要高。
但是也有些同学作为参与者1在第一步就选择了D,这或许也有他的道理,因为他担心自己根据逆向归纳法推出选择U后,参与者2不按常理出牌选择r的话自己就损失比较大。即害怕参与者2把事情搞砸。
现在我们画出4*2的收益矩阵,来分析其中的纳什均衡。
l r
Uu 4,3 1,2
Ud 3,1 1,2
Du 2,1 2,1
Dd 2,1 2,1
3个纳什均衡 [Uu,l](BE)、 [Du, r] 和[Dd, r]。
哪个均衡满足子博弈均衡的要求?
首先看一个小的子博弈(图1中蓝色框框中的部分),只有参与者1的博弈,他可以选择u或者d,NE:[u],在上面的三个纳什均衡中第三个[Dd, r]对应的该子博弈中的选择为d,不满足子博弈完美均衡(SPE)的定义,均衡3被排除。
接下来我们看看另一个子博弈(图1中红色框框中的部分),我们暂时不考虑混合策略,这里的pure NE: [u, l]和[d, r],均衡2被排除,因为他在该子博弈中并不是纳什均衡的。
因此只有均衡1[Uu, l]满足要求,而且只有它满足逆向归纳法。
结论1:子博弈完美均衡与逆向归纳法的预测是一致的。
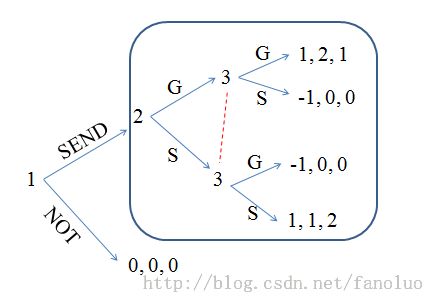
案例二:The matchmaker game
其中参与者1为Jack,可以选择是否撮合David和Nina,而David和Nina的选择可以是S和G任意一门课程。
从最后一个子博弈(蓝色框框中的部分)开始逆推,这个子博弈其实就是性别大战。pure NE: [G, G]和[S, S],这两个均衡给参与者1带来的收益都是1。我们再回到整个博弈,可以看到参与者1会选择SEND。
其实,上面这个子博弈中还有一个混合策略均衡[(2/3,1/3), (1/3, 2/3)],如果Jack成全David和Nina,那么他们碰面的概率是4/9,不会碰面的概率是5/9,也就是说Jack撮合这对的期望收益是1*4/9 -1*5/9 = -1/9,而他不撮合的话收益为0,因此这里第三个纳什均衡是[NOT, mix, mix]。
结论2:要求子博弈完美均衡,先求出每个子博弈的均衡,然后根据收益往回看。
案例三:经典的商学院案例,Strategic Investment
两家公司A和B,处于古诺竞争中,价格与需求曲线:2 - 1/3 * (qA+qB),每吨的生产成本是1美元。
回顾一下古诺均衡的产量 Q* =(a-c)/3b,在这里a = 2, c = 1, b = 1/3, Q* = 1(百万吨),p* = 4/3,均衡利润:(4/3 -1) * 1 = 1/3。
那么问题来了,现在有一台新机器,它有以下三个特性:(1)仅适用于A公司,(2)每年租金0.7百万美元,(3)可以把A的成本降低到0.5美元。
To rent or notto rent?
下面我们从三个角度来看看这个问题:
1. 会计师会怎么回答这个问题?
很简单的算术:根据上面的古诺均衡我们可以看到A公司每年产出1百万吨,每吨节省0.5美元,每年节省50万。而新机器的租用成本是70万,所以不该租用。
这个回答很boring,而且它是错误的。因为他假设租用了新机器后产量还是跟之前一样。
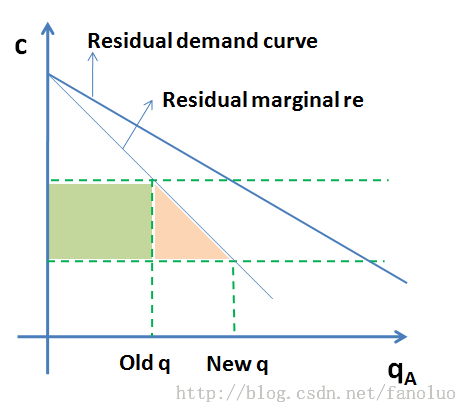
2. 经济学家如何看?
画出剩余需求曲线
我们从图中可以看出随着成本的降低,公司A的产量会增加,而会计师只计算了图中绿色矩形中的面积,其实还应该加上红色三角形的面积。0.5 + 0.19 = 0.69 < 0.7,结论仍然是not rent。
但是这个结果依然是错误的,因为B公司也可能改变他的产量。
3. Game theory answer
画出古诺竞争qA和qB的最佳对策曲线
公司A的最佳对策需要向右移动,当A公司增产时,B公司应该减产(strategysubstitute),A选择是否租用新机器,然后与B公司进行古诺竞争子博弈,如果你投资了会怎么样,然后从子博弈的收益回来再看是否租用。
博弈论者的答案是还可以增加31万的利润,0.31 +0.69 > 0.7 ,结论应该是租用。
结论3:我们应该考虑战略效应,即其他参与人也会改变行为。