数据结构（1）—— 排序算法汇总

最近很多同学问我关于排序算法的问题，像冒泡排序，选择排序。学过数据结构的还好说，对于没有接触过数据结构的同学来说内心基本是属于崩溃的。下面我就来总结一下数据结构中的八大排序算法。

概述

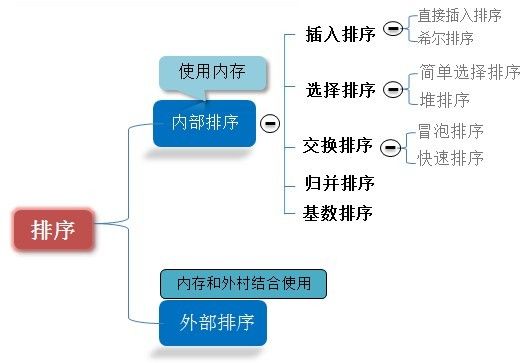
排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

我们这里说的八大排序就是内部排序

排序相关的概念

排序（按关键字大小顺序排列数据）。
排序方法：内部排序，外部排序；简单的排序方法O(n2)，先进的排序方法O(nlogn)，基数排序O(dn)；插入排序，交换排序，选择排序，归并排序，计数排序。
排序方法的稳定性：取决于该方法采取的策略，不是由一次具体的排序结果决定的。但是通过列举不稳定的排序实例可以说明该排序算法的不稳定性。
1、直接插入排序
直接插入排序是由两层嵌套循环组成的。外层循环标识并决定待比较的数值。内层循环为待比较数值确定其最终位置。直接插入排序是将待比较的数值与它的前一个数值进行比较，所以外层循环是从第二个数值开始的。当前一数值比待比较数值大的情况下继续循环比较，直到找到比待比较数值小的并将待比较数值置入其后一位置，结束该次循环。
将待排序记录插入已排好的记录中，不断扩大有序序列。一句话，“将待排序记录插入有序序列，重复n-1次” 。

例：排序前: 6 3 3 5 6 3 1 0 6 4
i = 0: 6
i = 1: 3 6
i = 2: 3 3 6
i = 3: 3 3 5 6
i = 4: 3 3 5 6 6
i = 5: 3 3 3 5 6 6
i = 6: 1 3 3 3 5 6 6
i = 7: 0 1 3 3 3 5 6 6
i = 8: 0 1 3 3 3 5 6 6 6
i = 9: 0 1 3 3 3 4 5 6 6 6
排序后: 0 1 3 3 3 4 5 6 6 6

插入排序演示地址

算法实现

void InsertSort(int a[], int n)  
{  
    for(int i= 1; i<n; i++){  
        if(a[i] < a[i-1]){               //若第i个元素大于i-1元素，直接插入。小于的话，移动有序表后插入 
            int j= i-1;   
            int x = a[i];        //复制为哨兵，即存储待排序元素 
            a[i] = a[i-1];           //先后移一个元素 
            while(x < a[j]){  //查找在有序表的插入位置 
                a[j+1] = a[j];  
                j--; //元素后移 
            }  
            a[j+1] = x;      //插入到正确位置 
        }  
        print(a,n,i);           //打印每趟排序的结果 
    }  

} 

2、希尔排序
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法，先将待排序列分割成若干个子序列，分别进行直接插入排序，基本有序后再对整个序列进行直接插入排序。
步骤：
1. 分成子序列(按照增量dk)；
2. 对子序列排序(直接插入排序)；
3. 缩小增量，重复以上步骤，直到增量dk=1。
增量序列中最后一个增量一定是1，如：… 9, 5, 3, 2, 1和… 13, 4, 1。如没有明确说明增量序列可以选择… 3, 2, 1或… 5, 3, 2, 1。

算法说明

void ShellSort ( T a[], int n )
{
  dk = n/2;
  while ( dk>=1 ) {
    // 一趟希尔排序，对dk个序列分别进行插入排序
    for ( i=dk; i<n; i++ ) {
      x = a[i];
      for ( j=i-dk; j>=0 and x<a[j]; j-=dk )
        a[j+dk] = a[j];
      a[j+dk] = x;
    }
    // 缩小增量
    dk = dk/2;
  }
}

3、选择排序
设所排序序列的记录个数为n。i取1,2,…,n-1,从所有n-i+1个记录（Ri,Ri+1,…,Rn）中找出排序码最小的记录，与第i个记录交换。执行n-1趟 后就完成了记录序列的排序。
第i趟排序过程是在剩余的待排记录中选一个最小（大）的，放在第i个位置。
一句话，“在待排记录中选取最小的，交换到合适位置，重复n-1次” 。

算法实现

void SelectionSort ( T a[], int n )
{
  for ( i=0; i<n-1; i++ ) {
    k = i;
    for ( j=i+1; j<n; j++)
      if ( a[j]<a[k] )  k=j;  // 最小记录
    if ( k!=i )  a[i]<->a[k];//交换
  }
}

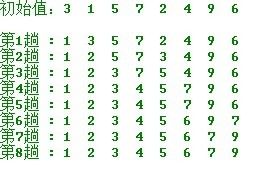
简单选择排序不愧简单之名，需要注意的是：
在简单选择排序过程中，所需移动记录的次数比较少。最好情况下，即待排序记录初始状态就已经是正序排列了，则不需要移动记录。
最坏情况下，即待排序记录初始状态是按第一条记录最大，之后的记录从小到大顺序排列，则需要移动记录的次数最多为3（n-1）。
时间复杂度O(n2)，耗费在比较记录上，比较次数始终为n(n-1)/2，移动次数最小为0，最大3(n-1)，即n-1次交换。
注意：简单选择排序是不稳定的。

4、冒泡排序
冒泡排序算法的运作如下：（从后往前）
比较相邻的元素。如果第一个比第二个大，就交换他们两个。对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。针对所有的元素重复以上的步骤，除了最后一个。持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

算法实现

void bubbleSort(int a[], int n){  
    for(int i =0 ; i< n-1; ++i) {  
        for(int j = 0; j < n-i-1; ++j) {  
            if(a[j] > a[j+1])  
            {  
                int tmp = a[j] ; 
                a[j] = a[j+1] ;  
                a[j+1] = tmp;  
            }  
        }  
    }  
} 

对冒泡排序常见的改进方法是加入一标志性变量，用于标志某一趟排序过程中是否有数据交换，如果进行某一趟排序时并没有进行数据交换，则说明数据已经按要求排列好，可立即结束排序，避免不必要的比较过程。本文再提供以下两种改进算法：

1．设置一标志性变量pos,用于记录每趟排序中最后一次进行交换的位置。由于pos位置之后的记录均已交换到位,故在进行下一趟排序时只要扫描到pos位置即可。

改进后算法如下:

void Bubble_1 ( int r[], int n) {  
    int i= n -1;  //初始时,最后位置保持不变 
    while ( i> 0) {   
        int pos= 0; //每趟开始时,无记录交换 
        for (int j= 0; j< i; j++)  
            if (r[j]> r[j+1]) {  
                pos= j; //记录交换的位置 
                int tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;  
            }   
        i= pos; //为下一趟排序作准备 
     }   
}   

2．传统冒泡排序中每一趟排序操作只能找到一个最大值或最小值,我们考虑利用在每趟排序中进行正向和反向两遍冒泡的方法一次可以得到两个最终值(最大者和最小者) , 从而使排序趟数几乎减少了一半。可以参考折半查找法

改进后的算法实现为:

    void Bubble_2 ( int r[], int n){  
        int low = 0;   
        int high= n -1; //设置变量的初始值 
        int tmp,j;  
        while (low < high) {  
            for (j= low; j< high; ++j) //正向冒泡,找到最大者 
                if (r[j]> r[j+1]) {  
                    tmp = r[j]; r[j]=r[j+1];r[j+1]=tmp;  
                }   
            --high;                 //修改high值, 前移一位 
            for ( j=high; j>low; --j) //反向冒泡,找到最小者 
                if (r[j]<r[j-1]) {  
                    tmp = r[j]; r[j]=r[j-1];r[j-1]=tmp;  
                }  
            ++low;                  //修改low值,后移一位 
        }   
    }   

好，今天先介绍这么多，剩下的改天再进行介绍。
剩下的还有快速排序、堆排序、归并排序、基数排序，有时间我们接着聊。

参考资料

• 严蔚敏，吴伟民．数据结构（c语言版）：清华大学出版社，1997.4
• 数据结构辅导讲义—庄波
• 百度百科