Machine Learning week 8 Dimensionality Reduction
Dimensionality Reduction
这是另外一种unsupervised learning
Motivation I: Data Compression
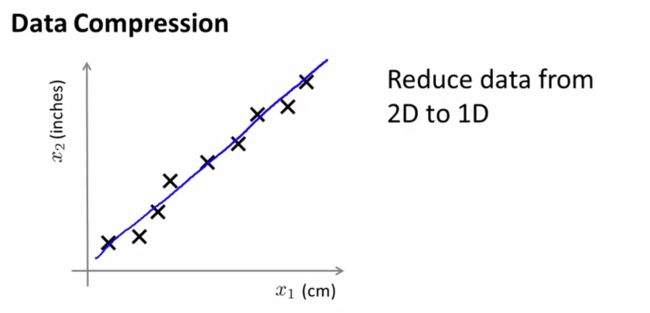
如下图,其中两个维度分别为厘米和英尺(四舍五入到整数英尺),而这两个维度的信息其实是高度冗余的信息。当我们有很多feature的时候,其中可能有一些feature之间有着很强的关联性
下面来看一下,如何压缩数据,下面我们画出图中的绿色线,也就是一条fit所有点的一条直线,然后把所有的点x向这条线上做投影,那么会得到新的点z,然后以这条绿线作为新的坐标系,每个z点都会有一个数字来代表它的坐标,这样我们就把x,从一个2维点转化为了1维点。
比如我们有很多1000维的数据,我们想要把它们变成100维空间的数据。或者我们想把它们变成3D或者2D的数据,以便我们可以把它们plot出来进行观察。
下面左1中我们找到一个比较好的贴合所有点的平面,中间图中,我们把所有点向中间的平面进行了投影,这个平面可以用两个向量表示,分别是z1和z2,然后我们的所有的点就都可以用z1和z2进行表示,成为一个2D的数据了。
Motivation: Data Visualization
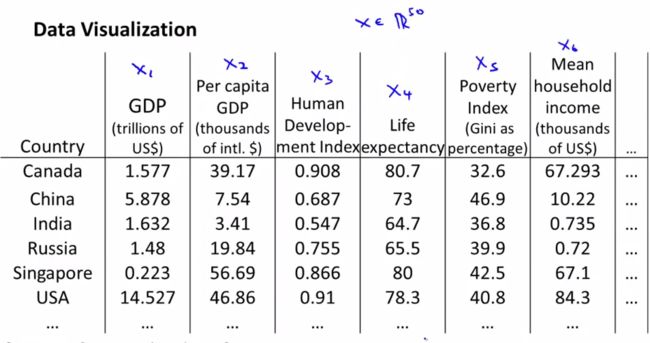
假如我们有很多国家的信息,每个国家都有15个维度的信息。如果能把这些信息plot出来的话,我们可以有更好的直观理解。
但是这么多的feature,我们很难把它们画出来,但是如果把这些信息转化成2D或者3D的信息的话,就可以画出来了。
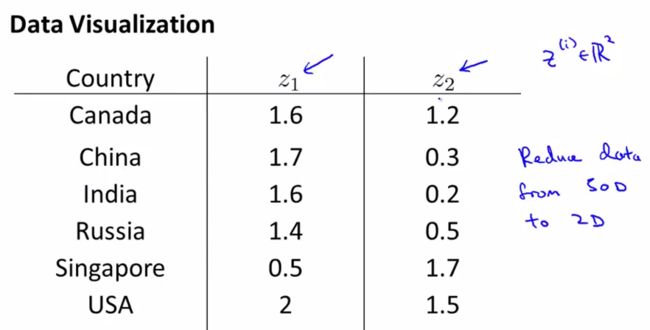
下面我们把这些信息转化成了2D的数据,但是我们难以只管了解到2个维度分别代表什么
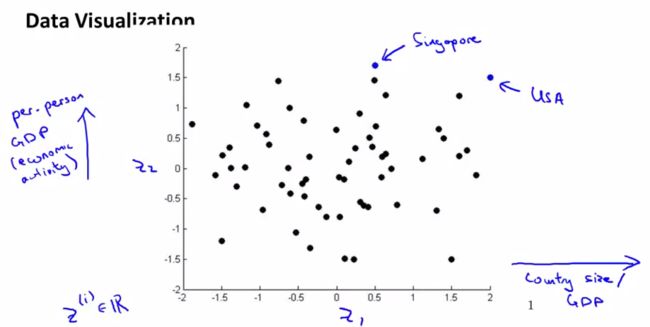
把数据plot出来,然后我们会发现横坐标和国家的整体GDP或者整体size对应,纵轴和人均Gdp对应
Principal Component Analysis Problem Formulation
PCA是最常使用的降维方法。
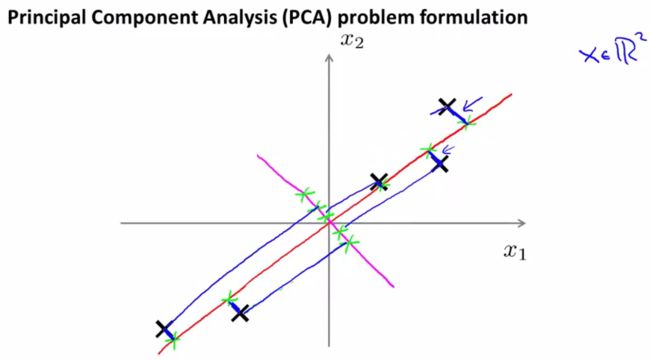
我们如何去选择一条直线来作为新的坐标呢,如下图,红色的线会是比较好的选择,因为每个点和点在线上的投影之间的距离的平方和很小,称为projection error。
而粉红色的线就不是一个好选择了。因为每个点到线的投影之间的距离都很大,对应的projection error也会很大
下面是PCA的比较官方的定义
其中向量的正负方向无所谓,只要代表的是同一个直线
对于3D的例子中,老师说u1和u2都是过原点的,这个很奇怪????
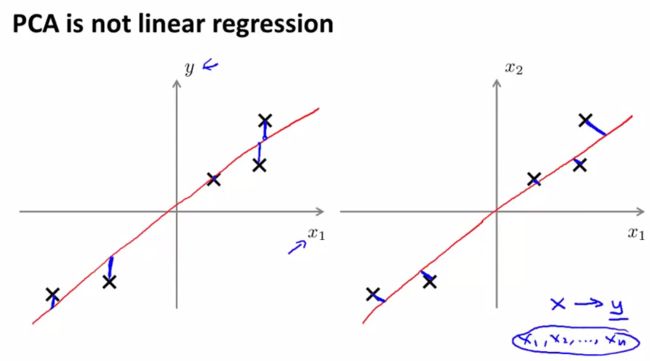
PCA并不是liner regression,首先他们的cost function的计算方法是不同的,左图是liner regression,计算的是y轴方向的误差,右图是PCA计算的是点和线之间最短距离的长度。另外一点就是liner regression中我们要预测y的值,但是PCA中是没有y存在的。
Principal Component Analysis algorithm
在进行PCA之前需要对数据进行处理,根据情况选择要不要进行feature scaling,但是mean normalization每次都要进行
PCA的目标就是要让projection error尽可能的小
下面是具体的算法
Σ(sigma)很不幸这个长的和求和符号一模一样。
sigma是一个nXn的矩阵
这里有2个方法对sigma进行矩阵分解分别是svd和eig,这里我们使用svd
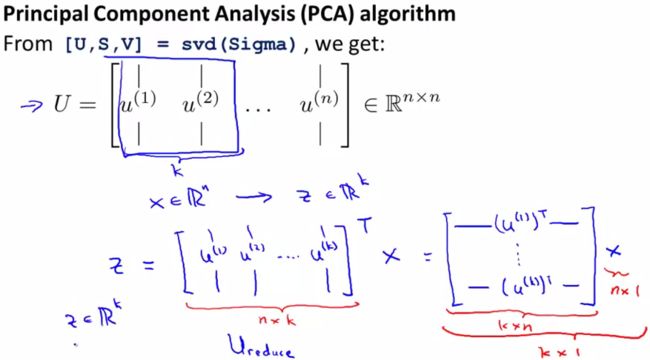
svd会返回3个结果。U是一个nXn的矩阵,如果要把n维降维到K的话,就取U的前K列
下一步就是如何得到k维空间表示的每个点了。公式如下,最终得到的z就是x的k维表示,
下面是梳理之后的PCA过程
加深一下对结果的理解:u的第k列会贡献力量计算出x在k维空间中k维上的分量
Choosing the number of Principal Components
下面引出了2个新的概念的定义。projection error和total variation。totoal variation代表每个点和原点的距离平方和。
以variance retained数值作为评估PCA的一个指标,一般来说95%-99%是比较常用的取值范围。即使取99%,也经常会取得很好的降维效果,因为很多的feature都有着很强的相关性。
下图左边是一个直观的逻辑,关于如何取得k的值,但是这样的计算量很大,索性svd有一个很好的特性,它的返回结果s可以用来计算variance retained数值
下面是总结之后的计算过程
Reconstruction from Compressed Representation
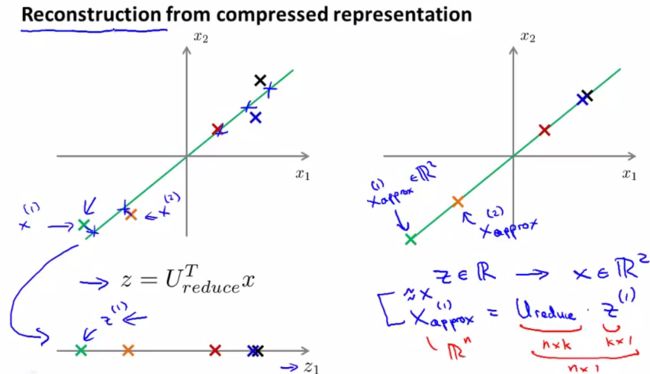
如何从z变回x呢,这被称为reconstruction。具体过程如下,但是必然会有一些失真。
Advice for Applying PCA
如果是supervised learning的话,首先把所有training set中的feature抽出来,不包括y,进行PCA降维,然后使用降维后的training set数据训练模型。如果再有新的数据进来的话,要使用已经获得的PCA先对数据进行降维,然后套入之前训练得到的模型中进行预测。
另外就是PCA的mapping关系是由training set决定的,cross validation和test data set的数据只能使用已经计算得到的PCA进行降维。
PCA降维之后的数据再训练得到的模型的精确性不会有很大的影响,但是运算数据会有很大的提升
上面的讲解中我们把PCA主要用在下面2个方面
但经常会有些不恰当的使用PCA的场景
比如使用PCA减少feature的数量,来防止overfitting。虽然效果可能不错。但是不推荐这样做。因为PCA降维的时候并没有考虑y的取值,也就是PCA扔掉了一些可能有用的信息,如果是出于组织overfitting的话,还是使用regularization更好
PCA并不是必须的一步,一般来说尽量不用PCA,毕竟会降低准确度。