使用回溯法求解数独问题，数独游戏算法

Title :

• 算法，数独问题
• 用概率算法中的拉斯维加斯算法实现数独问题的生成
• 用回溯法实现对数独问题的求解

注：数独问题与数度难题的区别是数度难题只有一个解，而数独问题的解有一个或多个。

Introduction :

标准的数独游戏是在一个 9 X 9 的棋盘上填写 1 – 9 这 9 个数字，规则是这样的：

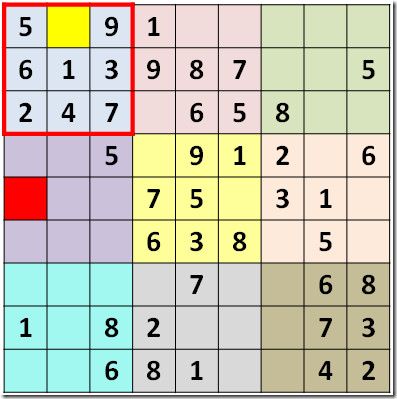
• 棋盘分成上图所示的 9 个区域（不同颜色做背景标出，每个区域是 3 X 3 的子棋盘），在每个子棋盘中填充 1 – 9 且不允许重复 ，下面简称块重复
• 每一行不许有重复值 ，下面简称行重复
• 每一列不许有重复值 ，下面简称列重复

如上红色框出的子区域中的亮黄色格子只能填 8。

扩展阅读：http://en.wikipedia.org/wiki/Sudoku

Goals :

1. 随机生成数独问题，如果做成一个数独小游戏的话可以按游戏难易程度生成，比如有简单、中等、困难三个程度
2. 求解数独问题，根据生成的数独问题或者用户输入的数独问题求解出所有答案或者求解出不超过MAX个答案，因为某个问题可能含有上十万个解，用MAX约束找到MAX个答案后就不再找其它的答案

Idea :

有一种求解数独问题的方案是“候选数字法”，就是在待填充的格子中填写不会造成行重复、列重复、块重复的数字，有的时候存在多个这样的数字，那么我们可以随机选取一个，如果待填充的格子中填写任何一个数字都会造成某种重复的发生，则说明这个问题没有解，也就是这不是一个数独问题。如上图中红色框出区域的下面一个区域的红色格子中可以填写的数字为 4、8、9，那么它的候选数字就是4、8、9，你可以随机选一个填入。当所有的格子填充完后数独问题就解决了。

根据上述的这种候选数字法，我们可以用它来生成数独问题以及求解数独问题。

关于生成数独问题：

循环遍历 9 X 9 的数独格子，在遍历到的当前格子的候选数字中随机选取一个数字填入，如果当前格子没有了候选数字则清空所有已经填好的格子，重新再来。这是一个最简单的也是最容易理解的概率方法了。伪码如下：

   1: int[][] sudoku = new int[9][9]; //数独棋盘

   2: while(true) {

   3: label:

   4:     clearSudoku(); //清空所有已填数字, 每个格子置 0

   5:     for(int row = 0; row < 9; row++) {

   6:         for(int col = 0; col < 9; col++) {

   7:             //getCandidates(row, col) 获取当前格子的候选数字

   8:             //randomCandidate() 随机选取一个候选数字

   9:             if(getCandidates(row, col) != NULL) //如果有候选数字

  10:                 sudoku[row][col] = randomCandidate(getCandidates(row, col));

  11:             else

  12:                 goto label; //跳转到label那里清空格子重新来过

  13:         }

  14:     }

  15: }

关于求解数独问题：

同上， 不过这次不是采用随机算法，因为随机算法没法保证把所有的解都求出。利用回溯法把所有可能的情况都遍历，那么就可以求出所有的解。我们考虑下面的一个实例：

初始时，sudoku[0][0]格子的候选数字为2， 3，5， 6，如图标出，sudoku[4][0]的为2，4，5，其它如图。那么我们在填充sudoku[0][0]的时候不能按照随机来了，因为我们需要把所有的情况遍历的话，需要按一定顺序来，也就是从2开始来，因为一旦某个格子填充了一个候选数字后，其它格子的候选数字会发生变化，假设sudoku[0][0]填充了2，那么与sudoku[0][0]在同一行、同一列、同一块内的格子的候选数字就不能再有2了，sudoku[4][0]、sudoku[6][0]等都应该将原来含有的2给删掉。

我们遍历着填写候选数字，当遇到某个格子的候选数字不存在的时候，我们应该回溯了，我们回到上一格，填写另一个候选数字。比如上图，我们按照这样的顺序来：

1. sudoku[0][0]填写2，sudoku[4][0]候选为(4,5)，sudoku[6][0]候选为(3, 5)，sudoku[7][0]候选为(4, 5, 6)，sudoku[8][0]候选为(5, 6)；
2. sudoku[4][0]填写4，sudoku[6][0]候选为(3, 5)，sudoku[7][0]候选为(5, 6)，sudoku[8][0]候选为(5, 6)；
3. sudoku[6][0]填写5，sudoku[7][0]候选为(6)，sudoku[8][0]候选为(6)；
4. 那么sudoku[7][0]填了6之后sudoku[8][0]就没有候选数字可填了

至于如何遍历所有的情况，我们可以这样来：

把候选数字都按大小从小到大排序，用一个栈记录已经选取过的候选数字在这个序列中的序号，每一次选取候选数字就入栈，每一次回溯就出栈。另外需要注意的是每一次改变格子数字的操作都需要更新候选数字。伪码如下（注意，这只是表达思想，代码在如果按执行顺序来是有误的）：

   1: Stack s;

   2: int idx;

   3: while(true) {

   4:     if(candidates[row][col] != NULL) {

   5:         //当前格子填写第idx个候选数字, idx = 0,1,2,3...

   6:         sudoku[row][col] = candidates[row][col](idx);

   7:         //如果所有的格子都填了，那么就把这个解保存起来，然后回溯

   8:         if(allBlanked()) {

   9:             solutions.add();

  10:             backtrace(row, col);

  11:         }

  12:         //idx入栈以记录已经填过的候选数字

  13:         s.push(idx);

  14:         //更新候选数字

  15:         updateCandidates();

  16:         //填写下一行

  17:         next(row, col);

  18:     }

  19:     else {//如果没有了候选数字就回到上一格填过的位置

  20:         backtrace(row, col);

  21:         //回溯到原点就结束

  22:         if(s.isEmpty()) {

  23:             end;

  24:         }

  25:         //获取上一格填写的数字的序号,这次应该填写下一个候选数字了,即序号加1

  26:         idx = s.pop() + 1;

  27:     }

  28: }

Result:

1: New game: 2: 0 7 0 0 8 0 0 2 3 3: 9 0 0 0 0 0 4 0 8 4: 0 8 3 0 0 0 5 9 0 5: 0 1 0 0 3 0 0 5 6 6: 0 9 0 0 5 0 2 0 0 7: 3 0 0 0 0 9 0 8 0 8: 7 2 0 0 0 8 0 0 0 9: 1 0 0 2 7 6 0 0 9 10: 8 0 0 3 9 5 0 0 0 11: 12: Solution: 1 13: 5 7 4 9 8 1 6 2 3 14: 9 6 1 5 2 3 4 7 8 15: 2 8 3 6 4 7 5 9 1 16: 4 1 7 8 3 2 9 5 6 17: 6 9 8 1 5 4 2 3 7 18: 3 5 2 7 6 9 1 8 4 19: 7 2 9 4 1 8 3 6 5 20: 1 3 5 2 7 6 8 4 9 21: 8 4 6 3 9 5 7 1 2 22: Solution: 2 23: 5 7 4 9 8 1 6 2 3 24: 9 6 1 5 2 3 4 7 8 25: 2 8 3 7 6 4 5 9 1 26: 4 1 7 8 3 2 9 5 6 27: 6 9 8 1 5 7 2 3 4 28: 3 5 2 6 4 9 1 8 7 29: 7 2 9 4 1 8 3 6 5 30: 1 3 5 2 7 6 8 4 9 31: 8 4 6 3 9 5 7 1 2 32: Solution: 3 33: 5 7 1 9 8 4 6 2 3 34: 9 6 2 5 1 3 4 7 8 35: 4 8 3 7 6 2 5 9 1 36: 2 1 4 8 3 7 9 5 6 37: 6 9 8 4 5 1 2 3 7 38: 3 5 7 6 2 9 1 8 4 39: 7 2 9 1 4 8 3 6 5 40: 1 3 5 2 7 6 8 4 9 41: 8 4 6 3 9 5 7 1 2 42: Solution: 4 43: 5 7 1 9 8 4 6 2 3 44: 9 6 2 5 1 3 4 7 8 45: 4 8 3 7 6 2 5 9 1 46: 2 1 8 4 3 7 9 5 6 47: 6 9 4 8 5 1 2 3 7 48: 3 5 7 6 2 9 1 8 4 49: 7 2 9 1 4 8 3 6 5 50: 1 3 5 2 7 6 8 4 9 51: 8 4 6 3 9 5 7 1 2 52: Solution: 5 53: 5 7 1 9 8 4 6 2 3 54: 9 6 2 5 1 3 4 7 8 55: 4 8 3 7 6 2 5 9 1 56: 2 1 8 4 3 7 9 5 6 57: 6 9 7 8 5 1 2 3 4 58: 3 5 4 6 2 9 1 8 7 59: 7 2 9 1 4 8 3 6 5 60: 1 3 5 2 7 6 8 4 9 61: 8 4 6 3 9 5 7 1 2

1: New game: 2: 7 6 1 8 0 4 9 0 0 3: 3 0 0 0 0 0 1 2 4 4: 0 5 2 0 0 0 0 7 8 5: 0 0 0 6 0 0 0 4 0 6: 0 0 9 1 0 0 7 0 0 7: 0 0 0 9 0 0 0 0 2 8: 0 0 0 2 0 0 0 5 6 9: 0 3 6 4 9 0 2 0 0 10: 0 2 0 0 6 0 4 9 0 11: 12: Solution: 1 13: 7 6 1 8 2 4 9 3 5 14: 3 9 8 7 5 6 1 2 4 15: 4 5 2 3 1 9 6 7 8 16: 1 7 5 6 3 2 8 4 9 17: 2 4 9 1 8 5 7 6 3 18: 6 8 3 9 4 7 5 1 2 19: 9 1 4 2 7 8 3 5 6 20: 5 3 6 4 9 1 2 8 7 21: 8 2 7 5 6 3 4 9 1 22: Solution: 2 23: 7 6 1 8 2 4 9 3 5 24: 3 9 8 7 5 6 1 2 4 25: 4 5 2 3 1 9 6 7 8 26: 1 7 3 6 8 2 5 4 9 27: 2 8 9 1 4 5 7 6 3 28: 6 4 5 9 3 7 8 1 2 29: 9 1 4 2 7 8 3 5 6 30: 5 3 6 4 9 1 2 8 7 31: 8 2 7 5 6 3 4 9 1 32: Solution: 3 33: 7 6 1 8 2 4 9 3 5 34: 3 9 8 7 5 6 1 2 4 35: 4 5 2 3 1 9 6 7 8 36: 1 7 5 6 3 2 8 4 9 37: 2 8 9 1 4 5 7 6 3 38: 6 4 3 9 7 8 5 1 2 39: 9 1 4 2 8 7 3 5 6 40: 5 3 6 4 9 1 2 8 7 41: 8 2 7 5 6 3 4 9 1 42: Solution: 4 43: 7 6 1 8 2 4 9 3 5 44: 3 9 8 7 5 6 1 2 4 45: 4 5 2 3 1 9 6 7 8 46: 1 7 5 6 3 2 8 4 9 47: 2 8 9 1 4 5 7 6 3 48: 6 4 3 9 8 7 5 1 2 49: 9 1 4 2 7 8 3 5 6 50: 5 3 6 4 9 1 2 8 7 51: 8 2 7 5 6 3 4 9 1 52: Solution: 5 53: 7 6 1 8 2 4 9 3 5 54: 3 9 8 5 7 6 1 2 4 55: 4 5 2 3 1 9 6 7 8 56: 2 1 3 6 5 7 8 4 9 57: 5 8 9 1 4 2 7 6 3 58: 6 4 7 9 3 8 5 1 2 59: 9 7 4 2 8 1 3 5 6 60: 1 3 6 4 9 5 2 8 7 61: 8 2 5 7 6 3 4 9 1 62: Solution: 6 63: 7 6 1 8 2 4 9 3 5 64: 3 9 8 5 7 6 1 2 4 65: 4 5 2 3 1 9 6 7 8 66: 2 1 7 6 3 8 5 4 9 67: 5 8 9 1 4 2 7 6 3 68: 6 4 3 9 5 7 8 1 2 69: 9 7 4 2 8 1 3 5 6 70: 1 3 6 4 9 5 2 8 7 71: 8 2 5 7 6 3 4 9 1 72: Solution: 7 73: 7 6 1 8 2 4 9 3 5 74: 3 9 8 5 7 6 1 2 4 75: 4 5 2 3 1 9 6 7 8 76: 2 1 3 6 5 7 8 4 9 77: 5 8 9 1 4 2 7 6 3 78: 6 7 4 9 3 8 5 1 2 79: 9 4 7 2 8 1 3 5 6 80: 1 3 6 4 9 5 2 8 7 81: 8 2 5 7 6 3 4 9 1 82: Solution: 8 83: 7 6 1 8 2 4 9 3 5 84: 3 9 8 5 7 6 1 2 4 85: 4 5 2 3 1 9 6 7 8 86: 5 1 7 6 3 2 8 4 9 87: 2 4 9 1 5 8 7 6 3 88: 6 8 3 9 4 7 5 1 2 89: 9 7 4 2 8 1 3 5 6 90: 1 3 6 4 9 5 2 8 7 91: 8 2 5 7 6 3 4 9 1

1: New game: 2: 2 0 0 0 0 3 0 7 0 3: 8 4 7 0 0 0 0 2 3 4: 5 3 0 0 8 0 0 0 0 5: 0 0 4 0 0 0 3 0 2 6: 1 2 0 0 0 0 0 0 0 7: 3 8 6 0 0 4 9 0 5 8: 0 0 0 0 1 0 2 0 0 9: 0 0 2 0 0 0 8 0 1 10: 7 1 3 0 0 0 0 0 0 11: 12: Solution: 1 13: 2 6 9 1 4 3 5 7 8 14: 8 4 7 5 6 9 1 2 3 15: 5 3 1 2 8 7 4 6 9 16: 9 7 4 6 5 1 3 8 2 17: 1 2 5 9 3 8 7 4 6 18: 3 8 6 7 2 4 9 1 5 19: 4 5 8 3 1 6 2 9 7 20: 6 9 2 4 7 5 8 3 1 21: 7 1 3 8 9 2 6 5 4 22: Solution: 2 23: 2 6 9 1 4 3 5 7 8 24: 8 4 7 5 6 9 1 2 3 25: 5 3 1 2 8 7 6 4 9 26: 9 7 4 6 5 1 3 8 2 27: 1 2 5 9 3 8 7 6 4 28: 3 8 6 7 2 4 9 1 5 29: 4 5 8 3 1 6 2 9 7 30: 6 9 2 4 7 5 8 3 1 31: 7 1 3 8 9 2 4 5 6 32: Solution: 3 33: 2 6 9 1 4 3 5 7 8 34: 8 4 7 5 9 6 1 2 3 35: 5 3 1 2 8 7 6 9 4 36: 9 7 4 6 5 1 3 8 2 37: 1 2 5 9 3 8 7 4 6 38: 3 8 6 7 2 4 9 1 5 39: 4 5 8 3 1 9 2 6 7 40: 6 9 2 4 7 5 8 3 1 41: 7 1 3 8 6 2 4 5 9 42: 43: ... 44: 45: Solution: 235 46: 2 6 9 5 4 3 1 7 8 47: 8 4 7 9 6 1 5 2 3 48: 5 3 1 7 8 2 6 4 9 49: 9 7 4 1 5 8 3 6 2 50: 1 2 5 3 9 6 7 8 4 51: 3 8 6 2 7 4 9 1 5 52: 6 9 8 4 1 5 2 3 7 53: 4 5 2 6 3 7 8 9 1 54: 7 1 3 8 2 9 4 5 6 55: Solution: 236 56: 2 6 9 5 4 3 1 7 8 57: 8 4 7 9 6 1 5 2 3 58: 5 3 1 7 8 2 4 9 6 59: 9 7 4 1 5 6 3 8 2 60: 1 2 5 8 3 9 7 6 4 61: 3 8 6 2 7 4 9 1 5 62: 6 9 8 3 1 5 2 4 7 63: 4 5 2 6 9 7 8 3 1 64: 7 1 3 4 2 8 6 5 9 65: Solution: 237 66: 2 6 9 5 4 3 1 7 8 67: 8 4 7 9 6 1 5 2 3 68: 5 3 1 7 8 2 6 9 4 69: 9 7 4 1 5 6 3 8 2 70: 1 2 5 8 3 9 7 4 6 71: 3 8 6 2 7 4 9 1 5 72: 6 9 8 4 1 5 2 3 7 73: 4 5 2 3 9 7 8 6 1 74: 7 1 3 6 2 8 4 5 9

Implementations : （代码是大二学期末的算法分析课程实习上写的，纯原创，当时用Qt写过一个界面设计了一个数独游戏，但是出于当时时间紧张没有做得很好，所以这里就不贴了，等以后有空完善好了再在Qt栏目里面贴出来，因为当时的代码存在小漏洞，这个版本修改了那个漏洞，原博文出于我的网易博客，因为今天是10月的最后一天了，再不加一篇博文，首页的那个“恒”就没了 = =！）

Qt游戏的那个截图：

Java源码：http://my.csdn.net/my/code/detail/14785

Java测试源码：http://my.csdn.net/my/code/detail/14787

	@Ggicci 本文属于个人学习笔记，如有错误，希望您能指正！转载请注明出处，谢谢 :) [CSDN博客]