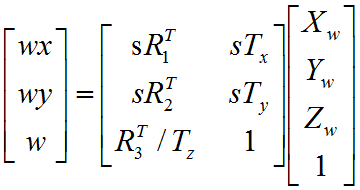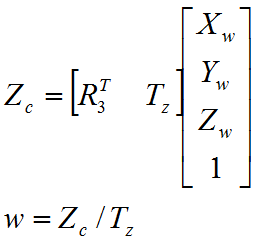POSIT算法的原理--opencv 3D姿态估计

3D姿态估计-POSIT算法

 

POSIT算法，Pose from Orthography and Scaling with Iterations， 比例正交投影迭代变换算法：

用于估计物体的3D姿态（相对于镜头的平移和旋转量）。算法正常工作的前提是物体在Z轴方向的“厚度”远小于其在Z轴方向的平均深度，比如距离镜头10米远的一张椅子。

 

算法流程：

假设待求的姿态，包括旋转矩阵R和平移向量T，分别为

透视投影变换为：

 

上式中的f是摄像机的焦距，它的具体值并不重要，重要的是f与x和y之间的比例，根据摄像头内参数矩阵的fx和fy可以得到这个比例。实际的运算中可直接令f=1，但是相应的x和y也要按照比例设定。比如，对于内参数为[fx,fy,u0,v0]的摄像头，如果一个像素的位置是(u,v)，则对应的x和y应为

设世界坐标系中的一点为(X_w,Y_w,Z_w)，则

有必要再解释一下旋转矩阵R和平移向量T的具体意义：

R的第i行表示摄像机坐标系中的第i个坐标轴方向的单位向量在世界坐标系里的坐标；

R的第i列表示世界坐标系中的第i个坐标轴方向的单位向量在摄像机坐标系里的坐标；

T正好是世界坐标系的原点在摄像机坐标系的坐标，特别的，Tz就代表世界坐标系的原点在摄像机坐标系里的“深度”。

根据前面的假设，物体在Z轴方向的‘厚度’，即物体表面各点在摄像机坐标系中的Z坐标变化范围，远小于该物体在Z轴方向的平均深度。一定要注意，“厚度”和“深度”都是相对于摄像机坐标系的Z轴而言的。当世界坐标系的原点在物体的中心附近时可以认为平均深度就是平移向量T中的Tz分量，即各点的Zc的平均值是Tz，而Zc的变化范围相对于Tz又很小，因此可以认为，Zc始终在Tz附近，Zc≈Tz。

根据这个近似关系，可得

这就是我们的迭代初值。在这种初始状态下，我们假设了物体的所有点在同一个深度上，这时的透视变换就退化为了一个比例正交投影POS。也就是，我们的迭代开始于一个比例正交投影，这也是POSIT算法名字的由来。

我们前面得到了：

由于我们给了w一个估计值，因此可以先将其看做已知量，删掉第三行（这样方程中就少了4个未知量，更方便求解），得到

由于w被看做已知，因此上面的迭代方程可以看做有8个未知量，分别是

给定一对坐标后（一个是世界坐标系的坐标，一个是图像坐标系的坐标，它们对应同一个点），我们就可以得到2个独立的方程，一共需要8个独立方程，因此至少需要给定4对坐标，而且对应的这4个点在世界坐标系中不能共面。为什么不能共面？如果第4个点与前三个点共面，那么该点的“齐次坐标”就可以被其他三个点的“齐次坐标”线性表示，而迭代方程的右侧使用的就是齐次坐标，这样由第四个点得到的方程就不是独立方程了。这里之所以强调“齐次坐标”是因为，只要三个点不共线，所有其他点（即使不共面）的“常规坐标”都可以被这三个点的“常规坐标”线性表示，但“齐次坐标”则要求共面。

OK，假如我们获得了4个不共面的点及其坐标，并通过迭代方程求出了8个未知量。这时我们就可以算出向量sR₁和sR₂的模长。而由于R₁和R₂本身都是单位向量，即模长为1。因此我们可以求出s，进而求得R₁和R₂以及Tz=f/s：

有了R₁和R₂就可以求出R₃，后者为前两个向量的叉积（两两垂直的单位向量）。

至此，整个旋转矩阵R和平移向量T，共12个未知量，就都求出来了。不过，这只是近似值，因为我们一开始时假设了w=1（或Zc=Tz），即物体上所有的点的深度都是Tz。现在我们有了一个近似的转换矩阵，可以利用它为各点计算一个新的深度，这个深度比Tz更准确。新的深度Zc和新的迭代系数w等于：

这时，由于每个点的有不同的深度，他们也就有了不同的迭代系数w。接着，将每个点的新w值代入迭代方程中，重新得到8个方程。由于这一次每个点的w（表征了深度信息）都比上一次迭代时更准确，因此会得到更精确的转换矩阵，而更精确的转换矩阵反过来又能让我们求得各点更精确的深度信息和w。如此往复循环反馈，就可逐步逼近精确解。

 

openCV里用cvPOSIT()函数实现POSIT迭代，具体的函数用法网上有很多介绍不再重复了。顺带提一下openCV里的另两个函数solvePNP()和cvFindExtrinsicCameraParams2()，这两个函数功能与POSIT类似，也是在已知一组点对应的图像坐标和世界坐标以及摄像头内参数的情况下计算物体的3D姿态，不过与POSIT不同的是，它们不是求近似解，而是直接求精确解。既然可以直接求精确解了，那POSIT估计算法还有什么意义呢？

其实理论上，只要获得3个点的信息，就可以得出旋转矩阵R和平移向量T了：

R和T共有12个未知量，每个点的坐标代入前面的“---原始方程--”中，消去w，可得到2个独立的方程，3个点就可以得到6个线性方程，再加上R自身的正交矩阵特征（每行、每列都是单位向量，模长为1）又可以得到6个独立的方程（非线性），共12个方程。

但实际中，解非线性方程很麻烦，所以openCV中应该是用了其他的优化方法。最无奈地，我们可以找6个点，每个点用“---原始方程--”消去w得到2个线性方程，最终也能得到12个方程，不过由于这种方法的求解过程中直接无视了正交矩阵R本身的特征，最后得到的结果会由于点坐标的测量误差和计算误差而稍微违反R自身的正交矩阵约束，当然这可以通过迭代弥补，但会增加算法的复杂度。可能有人会疑惑，同样是从3行的“---原始方程--”转化成2行的方程，为什么POSIT方法只需要四个点就可以求解，而这里却需要6个点？要知道，这里只是利用线性关系消去了w，但保留了原来第三行中的未知量，因此未知量的数量保持12不变；而POSIT方法中，直接为w选取了一个估计值，并删去了“---原始方程--”的第3行，这样方程中才少了4个未知量只剩下8个，所以利用4个点的坐标才得以求解。

于是，我们大概就能猜到既然有精确求解的算法却还要保留POSIT估计算法的原因了：如果只有少数点的信息（比如4个），又不想求解非线性方程，那就该POSIT上了。