HDU1081二维子数组最大和/压缩/动态规划/DP

HDU1081

To The Max

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 7307    Accepted Submission(s): 3532

Problem Description

Given a two-dimensional array of positive and negative integers, a sub-rectangle is any contiguous sub-array of size 1 x 1 or greater located within the whole array. The sum of a rectangle is the sum of all the elements in that rectangle. In this problem the sub-rectangle with the largest sum is referred to as the maximal sub-rectangle.
As an example, the maximal sub-rectangle of the array:
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
is in the lower left corner:
9 2
-4 1
-1 8
and has a sum of 15.

Input

The input consists of an N x N array of integers. The input begins with a single positive integer N on a line by itself, indicating the size of the square two-dimensional array. This is followed by N 2 integers separated by whitespace (spaces and newlines). These are the N 2 integers of the array, presented in row-major order. That is, all numbers in the first row, left to right, then all numbers in the second row, left to right, etc. N may be as large as 100. The numbers in the array will be in the range [-127,127].

Output

Output the sum of the maximal sub-rectangle.

Sample Input

    
    
    
    

     
     
     
     4
0 -2 -7 0 9 2 -6 2
-4 1 -4 1 -1
8 0 -2
    
    
    
    

Sample Output

    
    
    
    

     
     
     
     15
    
    
    
    

Source

Greater New York 2001

题目：题意大致是求二维数组的最大矩阵和。

例如：

0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

它的最大矩阵是
9 2
-4 1
-1 8

最大矩阵和是9+2-4+1-1+8=15

在之前的博客http://blog.csdn.net/linraise/article/details/9814153中有讨论到一维数组的子数组的最大和的求法(动态规划，

O(N)时间效率)现在我们碰到的是二维数组的子矩阵最大和，思路其实是一致的，也是动态规划，但是，需要先将二

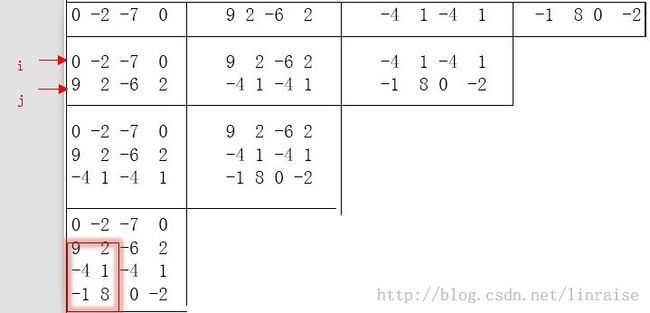
维压缩至一维。压缩的方式用一张图来说明：

上图中的每一个格子都需要压缩成一维（用另一个寄存数组累加每一个格子的对应列），用两个索引i,j指引压缩的行距从i到j。

对每一个压缩寄存数组都调用一维子数组求和函数。最终再求总的最大值即可。时间复杂度O(n^3)

#include <iostream>
#include <limits.h>
#include <string.h>
using namespace std;

int map[200][200]; //存图
int sub[200];		//寄存

int SubArr(int* Sub,int n)
{
	int i,CurSum = 0,Sum = INT_MIN;
	for(i=0; i < n; ++i)
	{
		if( CurSum < 0 )
			CurSum = Sub[i];
		else
			CurSum += Sub[i];
		if( CurSum > Sum )
			Sum = CurSum;
	}
	return Sum;
}
int MulSubArr(int n)
{
	int i,j,k,SubSum, Sum = INT_MIN;
	//memset(sub,0,sizeof(sub));
	for(i=0; i < n; ++i)
	{
		memset(sub,0,sizeof(sub));
		for(j=i; j < n; ++j)
		{
			for(k=0; k < n; ++k)
				sub[k] += map[j][k];

			SubSum = SubArr(sub,n);
			if ( SubSum > Sum )
				Sum = SubSum;
		}
	}
	return Sum;
}
int main()
{
	int n,i,j;
	while(cin >> n)
	{
		for(i=0; i < n; ++i)
		{
			for(j=0; j < n; ++j)
			{
				cin >> map[i][j];
			}
		}
		cout << MulSubArr(n) << endl;
	}
	return 0;
}