计算几何----判断线段相交（一）

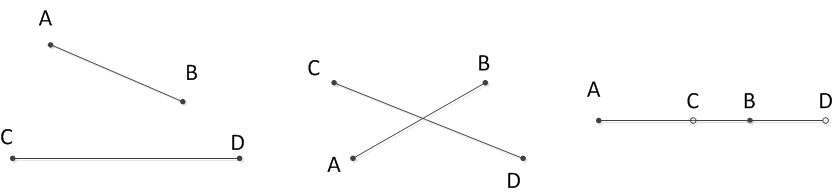
 判断线段相交：

两个线段的交点个数可能有0个 1个或者无数个

判断两个线段相交，可以按照如下步骤：

判断A点B点是否在线段CD的两侧，即计算叉积时异号

判断C点和D点是否在线段AB的两侧，即计算叉积时异号

然后在处理特殊情况，即ABCD四个点有至少三个点共线的情况，即出现叉积为零的情况，如果A点与线段CD共线，则要查看A点是否在线段CD上，其它情况依次类推。

3.下面是判断线段相交的程序：

# include <iostream>
# include <cstdlib>
using namespace std;
# define min(x,y)  ((x)<(y)?(x):(y))
# define max(x,y)    ((x)>(y)?(x):(y))
const int N=100001;
int n;
struct point
{
float x;
float y;
};

float direct(point i,point j,point k)     //计算叉积
{
	return (k.x-i.x)*(j.y-i.y)-(j.x-i.x)*(k.y-i.y);
}

int onsegment(point a,point b,point c)   //共线时，判断点是否落在线段上   
{
	float minx=min(a.x,b.x);
	float maxx=max(a.x,b.x);
	float miny=min(a.y,b.y);
	float maxy=max(a.y,b.y);
	return c.x>=minx&&c.x<=maxx&&c.y>=miny&&c.y<=maxy;
}
int f(point p1,point q1,point p2,point q2)
{
float d1=direct(p2,q2,p1);        
float d2=direct(p2,q2,q1);
float d3=direct(p1,q1,p2);
float d4=direct(p1,q1,q2);
if(d1*d2<0&&d3*d4<0)
	return true;
else if(d1==0&&onsegment(p2,q2,p1))
	return true;
else if(d2==0&&onsegment(p2,q2,q1))
	return true;
else if(d3==0&&onsegment(p1,q1,p2))
	return true;
else if(d4==0&&onsegment(p1,q1,q2))
	return true;
return false;
}
int main()
{
	point a={0,0};
	point b={2,2};
	point c={2,0};
	point d={0,2};
	cout<<f(a,b,c,d)<<endl; //输出 1 ，即线段相交 
	return 0;
}