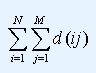【bzoj3994】[SDOI2015]约数个数和 莫比乌斯反演

Description

设d(x)为x的约数个数，给定N、M，求

Input

输入文件包含多组测试数据。

第一行，一个整数T，表示测试数据的组数。
接下来的T行，每行两个整数N、M。

Output

T行，每行一个整数，表示你所求的答案。

Sample Input

2

7 4

5 6

Sample Output

110

121

HINT

1<=N, M<=50000

1<=T<=50000

Source

Round 1 感谢yts1999上传

这题好高能…

先看一维的情况：

∑i<=nd(i)

=∑i<=n∑k<=i1[k|i]

=∑k<=n⌊nk⌋

然后有一个结论：

d(i∗j)=∑p|i∑q|j1[gcd(p,q)=1]

为什么呢？我是这样想的：如果一个数是i*j的约数，那么这个数一定是i的某一个约数p和j的某一个约数q的乘积，但因为有重复，所以我们可以只统计gcd(p,q)=1的数，因为任何数都可以被两个互质的数相乘来表示。同样这样的p和q一定存在于i和j的约数中，因为唯一分解定理。

脑洞出这个就可以继续推导了。这里写详细点。

∑i<=n∑j<=md(i∗j)

=∑i<=n∑j<=m∑p|i∑q|j1[gcd(p,q)=1]

=∑p<=n∑q<=m1[gcd(p,q)=1]∗⌊np⌋∗⌊mq⌋

为了方便，把p换成i，q换成j。

∑i<=n∑j<=m1[gcd(i,j)=1]∗⌊ni⌋∗⌊mj⌋

=∑i<=n∑j<=me(gcd(i,j))∗⌊ni⌋∗⌊mj⌋

=∑i<=n∑j<=m∑d|i & d|jμ(d)∗⌊ni⌋∗⌊mj⌋

=∑d<=nμ(d)∑i<=n∗⌊ni⌋[d|i]∑j<=m∗⌊mj⌋[d|j]

=∑d<=nμ(d)∑i<=n/d∗⌊nid⌋∑j<=m/d∗⌊mjd⌋

=∑d<=nμ(d)∗f(⌊nd⌋)∗f(⌊md⌋)

其中 f(n)=∑i<=n⌊ni⌋

我们发现 f 正好是 d 的前缀和，这样筛出来d和mu，求mu和d的前缀和，就能 O(sqrt(n)) 回答了。

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int SZ = 1000010;

typedef long long LL;

bool vis[SZ];

int pri[SZ],d[SZ],mu[SZ],cnt[SZ],sum_mu[SZ];
LL f[SZ];
void gen(int n)
{
    d[1] = 1;
    mu[1] = 1;
    for(int i = 2,tot = 0;i <= n;i ++)
    {
        if(!vis[i]) pri[++ tot] = i,mu[i] = -1,d[i] = 2,cnt[i] = 1;
        for(int j = 1,m;j <= tot && (m = i * pri[j]) <= n;j ++)
        {
            vis[m] = 1;
            if(i % pri[j] == 0)
            {
                mu[m] = 0;
                cnt[m] = cnt[i] + 1;
                d[m] = d[i] / (cnt[i] + 1) * (cnt[m] + 1);
                break;
            }
            else
            {
                mu[m] = -mu[i];
                cnt[m] = 1;
                d[m] = d[i] << 1;
            }
        }
    }
    for(int i = 1;i <= n;i ++)
    {
        sum_mu[i] = sum_mu[i - 1] + mu[i];
        f[i] = f[i - 1] + d[i];
    }
}

LL ask(int n,int m)
{
    if(n > m) swap(n,m);
    LL ans = 0;
    for(int i = 1,r;i <= n;i = r + 1)
    {
        r = min(n / (n / i),m / (m / i));
        ans += (LL)(sum_mu[r] - sum_mu[i - 1]) * f[n / i] * f[m / i];
    }
    return ans;
}

int main()
{
    int T;
    scanf("%d",&T);
    gen(50000);
    while(T --)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        printf("%lld\n",ask(n,m));
    }
    return 0;
}