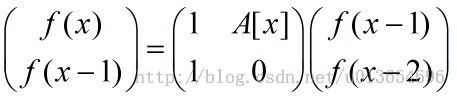ZOJ 3772 Calculate the Function( 线段树 )
题意:
给一个序列An
有m个询问,每个询问包括l和r
定义f(l) = a[l], f(l+1) = a[l+1], f(x)=f(x-1) + a[x] * f(x-2), x >= l + 2;
对每个询问,求f(r);
当x>=l+2时,
f(x)=f(x-1) + a[x]* f(x-2), 所以就有递推式
所以当r>=l+1时,
然后就可以先求出:
用线段树就可以在O(logn)的时间求出这个式子,不过线段树的每个节点保存的是一个矩阵
还有就是要注意矩阵乘的方向
总的复杂度是O(nlogn+mlogn)
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<set>
#include<map>
#include<queue>
#include<vector>
#include<cstdlib>
#include<stack>
using namespace std;
#define inf 0x3f3f3f3f
#define eps 1e-7
#define LL long long
#define ULL unsigned long long
#define MP make_pair
#define pb push_back
#define ls ( i << 1 )
#define rs ( ls | 1 )
#define md ( ( ll[i] + rr[i] ) >> 1 )
#define mxn 400010
#define mod 1000000007
#define PI acos( -1.0 )
struct mat {
LL a[2][2];
mat() {
memset( a, 0, sizeof( a ) );
}
mat( LL x ) {
a[0][0] = a[1][0] = 1;
a[1][1] = 0;
a[0][1] = x;
}
mat operator * ( const mat &b ) const {
mat ret;
for( int i = 0; i < 2; ++i )
for( int j = 0; j < 2; ++j )
for( int k = 0; k < 2; ++k )
ret.a[i][j] = ( ret.a[i][j] + a[i][k] * b.a[k][j] ) % mod;
return ret;
}
};
int ll[mxn], rr[mxn];
LL arr[mxn];
mat sum[mxn];
void build( int l, int r, int i ) {
ll[i] = l, rr[i] = r;
if( l == r ) {
sum[i] = mat( arr[l] );
return;
}
build( l, md, ls );
build( md + 1, r, rs );
sum[i] = sum[rs] * sum[ls];
}
mat query( int l, int r, int i ) {
if( ll[i] == l && rr[i] == r ) {
return sum[i];
}
if( r <= md )
return query( l, r, ls );
if( l > md )
return query( l, r, rs );
return query( md + 1, r, rs ) * query( l, md, ls );
}
mat t;
int main() {
//freopen( "tt.txt", "r", stdin );
int n, m;
int cas;
scanf( "%d", &cas );
while( cas-- ) {
scanf( "%d%d", &n, &m );
for( int i = 1; i <= n; ++i )
scanf( "%lld", &arr[i] );
build( 1, n, 1 );
while( m -- ) {
int l, r;
scanf( "%d%d", &l, &r );
if( r == l || r == l + 1 ) {
printf( "%lld\n", arr[r] );
continue;
}
t = query( l + 2, r, 1 );
printf( "%lld\n", ( t.a[0][0] * arr[l+1] + t.a[0][1] * arr[l] ) % mod );
}
}
return 0;
}