POJ 1703 Find them, Catch them【带权并查集】

Find them, Catch them

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 39679		Accepted: 12195

Description

The police office in Tadu City decides to say ends to the chaos, as launch actions to root up the TWO gangs in the city, Gang Dragon and Gang Snake. However, the police first needs to identify which gang a criminal belongs to. The present question is, given two criminals; do they belong to a same clan? You must give your judgment based on incomplete information. (Since the gangsters are always acting secretly.) 

Assume N (N <= 10^5) criminals are currently in Tadu City, numbered from 1 to N. And of course, at least one of them belongs to Gang Dragon, and the same for Gang Snake. You will be given M (M <= 10^5) messages in sequence, which are in the following two kinds: 

1. D [a] [b] 
where [a] and [b] are the numbers of two criminals, and they belong to different gangs. 

2. A [a] [b] 
where [a] and [b] are the numbers of two criminals. This requires you to decide whether a and b belong to a same gang. 

Input

The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case begins with a line with two integers N and M, followed by M lines each containing one message as described above.

Output

For each message "A [a] [b]" in each case, your program should give the judgment based on the information got before. The answers might be one of "In the same gang.", "In different gangs." and "Not sure yet."

Sample Input

1
5 5
A 1 2
D 1 2
A 1 2
D 2 4
A 1 4

Sample Output

Not sure yet.
In different gangs.
In the same gang.

题目大意：一共有两种犯罪团伙，请你编程判断询问的两个犯罪嫌疑人是否在一个团伙，或者不知道。

两种操作，对于A X Y表示查询XY是否是一个团伙的。对于D X Y 表示X和Y不在一个团伙。

构建思路过程+详解：

对于给定操作D X Y 我们能够知道X Y不属于一个团伙，我们知道，普通的并查集是将一些个元素合并在一个集合里边，通常用来表示一个集合。但是现在给出的条件是不同的团伙，一时间显得有些蒙蔽。。。。不锅不要担心，我们线性考虑一下这个问题我们就会有思路的构建点：

假如我们有两个已知条件，1和2属于不同团伙，2和3属于不同同伙，显然，1和3是同伙并且和2不是同伙。这个时候我们其实还是可以用一个并查集将这已知的两条无向边都建入一个集和中，那么为了区分团伙，我们需要对其边进行赋值。12赋值为1,23赋值为1，假设我们在合并的时候选取1为根节点，那么13权值为2.不难发现，如果是一个团伙，其边权值为偶数，如果不是一个同伙，边权值为奇数。并且我们只要选取了每个节点作为参考点，对于其他子节点都计算从子节点到根节点的距离，那么就可以算出子节点和子节点之间的关系了。

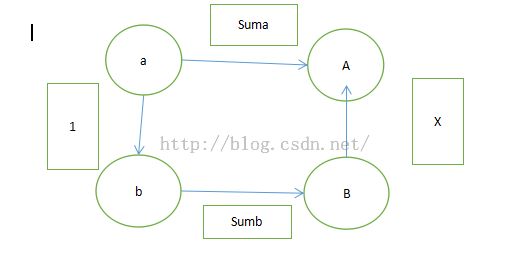
那么我们如何处理合并操作呢？我们已知a，b权值为1，假设a到其根节点A距离为suma，b到其根节点B距离为sumb，我们能够简单的画出这样一个图：

显而易见，1+sumb==x+suma，这样我们就能知道x的值为1+sumb-suma。

那么求子节点到子节点的距离也很容易（当然是一定要在一个集合里边）：suma-sumb即可。如果其值为偶数，那么说明他们是同伙，否则为非同伙。

注意点：当N==2的时候直接询问A 1 2的时候要输出different，因为题干中有说明每个团伙至少有一个人。

AC代码：

#include<stdio.h>
#include<string.h>
using namespace std;
int sum[100050];
int f[100050];
int vis[100050];
int find(int x)
{
    if(x!=f[x])
    {
        int pre=f[x];//pre是x的一个父节点。
        f[x]=find(f[x]);//递归找祖先。
        sum[x]+=sum[pre];//路径压缩部分。
    }
    return f[x];
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
        {
            f[i]=i;
            sum[i]=0;
        }
        while(m--)
        {
            char s[5];
            scanf("%s",s);
            int x,y;
            scanf("%d%d",&x,&y);
            if(s[0]=='A')
            {
                int xx=find(x);
                int yy=find(y);
                if(xx==yy)
                {
                    if((sum[y]-sum[x])%2==0)
                    {
                        printf("In the same gang.\n");
                    }
                    else printf("In different gangs.\n");
                }
                else
                {
                    if(n==2)
                    printf("In different gangs.\n");
                    else
                    printf("Not sure yet.\n");
                }
            }
            if(s[0]=='D')
            {
                int xx=find(x);
                int yy=find(y);
                if(xx!=yy)
                {
                    sum[yy]=1-sum[y]+sum[x];
                    f[yy]=xx;
                }
            }
        }
    }
}