三阶贝塞尔曲线Interpolator的应用

前期知识储备

• 贝塞尔曲线的介绍
• 关于Interpolator
• 影响动画的缓动函数

想实现缓动函数中的动画效果，发现很多都是贝塞尔方程实现的

所以现在需要实现它

贝塞尔曲线三阶方程

B(t)=(1−t)3P0+3(1−t)2tP1+3(1−t)t2P2+t3P3，t∈[0,1]

（4个点确定的，起点P0，两个控制点P1、P2，终点P3）

首先我们要重写Interpolator 中的getInterpolation（）方法

@Override
public float getInterpolation(float input) {
}

input 时间因子是介于0、1之间的，返回的值也是介于0，1之间的
也就是贝塞尔方程的x，y也是介于0，1之间

所以起点（0，0）终点（1，1）
简化后的三阶方程

x=3(1−t)2tP1.x+3(1−t)t2P2.x+t3，t∈[0,1]

y=3(1−t)2tP1.y+3(1−t)t2P2.y+t3，t∈[0,1]

input就是x， （P1.x,P1.y）,（P2.x,P2.y）分别是P1,P2的坐标 ，y就是函数要求返回的（这就是我们要计算的）

思路是这样的已知x可求 t，根据t得出y

第一步：写出方程函数

 public static double cubicEquation(double t, double p1, double p2) {
        double u = 1 - t;
        double tt = t * t;
        double uu = u * u;
        double ttt = tt * t;
        return 3 * uu * t * p1 + 3 * u * tt * p2 + ttt;
    }

第二步：求解t（这步其实需要证明 x在t处于[0,1]区间上是递增的）

  // 近似求解t
        double tempX;
        for (int i = mLastI; i < 4096; i++) {
            t =i * STEP_SIZE;
            tempX = cubicEquation(t, point1.x, point2.x);
            if (tempX >= input) {
                mLastI = i;
                break;
            }
        }

第三步：求y

  value = cubicEquation(t, point1.y, point2.y);

这样很多缓动动画效果都可以实现了
通过这个网址可以编辑和查看动画效果

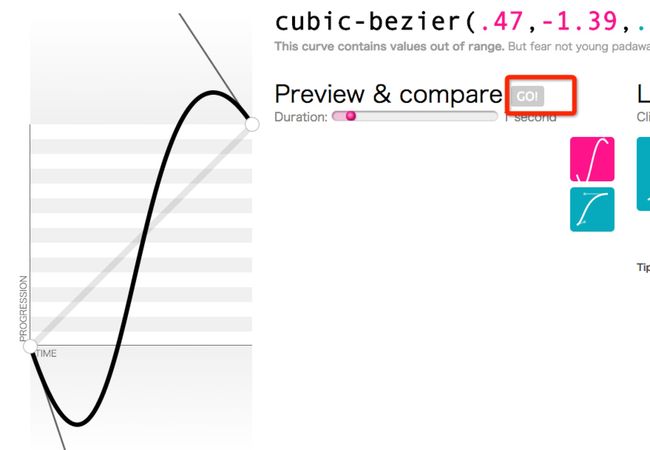
public class CubicBezierInterpolator implements Interpolator {
    private int mLastI = 0;
    private static final float STEP_SIZE = 1.0f / 4096;
    private final PointF point1 = new PointF();
    private final PointF point2 = new PointF();

    public CubicBezierInterpolator(float x1, float y1, float x2, float y2) {
        point1.x = x1;
        point1.y = y1;
        point2.x = x2;
        point2.y = y2;
    }

    @Override
    public float getInterpolation(float input) {
        float t = input;
        //如果重新开始要重置缓存的i。
        if (input == 0) {
            mLastI = 0;
        }
        // 近似求解t
        double tempX;
        for (int i = mLastI; i < 4096; i++) {
            t = i * STEP_SIZE;
            tempX = cubicEquation(t, point1.x, point2.x);
            if (tempX >= input) {
                mLastI = i;
                break;
            }
        }
        double value = cubicEquation(t, point1.y, point2.y);

        //如果结束要重置缓存的i。
        if (input == 1) {
            mLastI = 0;
        }
        return (float) value;
    }

    public static double cubicEquation(double t, double p1, double p2) {
        double u = 1 - t;
        double tt = t * t;
        double uu = u * u;
        double ttt = tt * t;
        return 3 * uu * t * p1 + 3 * u * tt * p2 + ttt;
    }

}

补充：一般方程式
n阶方程

B(t)=limx=0nCin(1−t)n−itnPi，t∈[0,1]

最后的最后 Android里源码里也有一个实现贝塞尔插值器的利用的是对曲线上点的枚举,不过控制点是固定的
然后精确度就是枚举数组的大小

/** * A pre-baked bezier-curved interpolator for indeterminate progress animations. */
final class BakedBezierInterpolator implements Interpolator {
    private static final BakedBezierInterpolator INSTANCE = new BakedBezierInterpolator();

    public final static BakedBezierInterpolator getInstance() {
        return INSTANCE;
    }

    /** * Use getInstance instead of instantiating. */
    public BakedBezierInterpolator() {
        super();
    }

    /** * Lookup table values. * Generated using a Bezier curve from (0,0) to (1,1) with control points: * P0 (0,0) * P1 (0.4, 0) * P2 (0.2, 1.0) * P3 (1.0, 1.0) * <p/> * Values sampled with x at regular intervals between 0 and 1. */
    private static final float[] VALUES = new float[]{
            0.0f, 0.0002f, 0.0009f, 0.0019f, 0.0036f, 0.0059f, 0.0086f, 0.0119f, 0.0157f, 0.0209f,
            0.0257f, 0.0321f, 0.0392f, 0.0469f, 0.0566f, 0.0656f, 0.0768f, 0.0887f, 0.1033f, 0.1186f,
            0.1349f, 0.1519f, 0.1696f, 0.1928f, 0.2121f, 0.237f, 0.2627f, 0.2892f, 0.3109f, 0.3386f,
            0.3667f, 0.3952f, 0.4241f, 0.4474f, 0.4766f, 0.5f, 0.5234f, 0.5468f, 0.5701f, 0.5933f,
            0.6134f, 0.6333f, 0.6531f, 0.6698f, 0.6891f, 0.7054f, 0.7214f, 0.7346f, 0.7502f, 0.763f,
            0.7756f, 0.7879f, 0.8f, 0.8107f, 0.8212f, 0.8326f, 0.8415f, 0.8503f, 0.8588f, 0.8672f,
            0.8754f, 0.8833f, 0.8911f, 0.8977f, 0.9041f, 0.9113f, 0.9165f, 0.9232f, 0.9281f, 0.9328f,
            0.9382f, 0.9434f, 0.9476f, 0.9518f, 0.9557f, 0.9596f, 0.9632f, 0.9662f, 0.9695f, 0.9722f,
            0.9753f, 0.9777f, 0.9805f, 0.9826f, 0.9847f, 0.9866f, 0.9884f, 0.9901f, 0.9917f, 0.9931f,
            0.9944f, 0.9955f, 0.9964f, 0.9973f, 0.9981f, 0.9986f, 0.9992f, 0.9995f, 0.9998f, 1.0f, 1.0f
    };

    private static final float STEP_SIZE = 1.0f / (VALUES.length - 1);

    @Override
    public float getInterpolation(float input) {

        long a=System.nanoTime();
        if (input >= 1.0f) {
            return 1.0f;
        }

        if (input <= 0f) {
            return 0f;
        }

        int position = Math.min(
                (int) (input * (VALUES.length - 1)),
                VALUES.length - 2);

        float quantized = position * STEP_SIZE;
        float difference = input - quantized;
        float weight = difference / STEP_SIZE;
        float result=VALUES[position] + weight * (VALUES[position + 1] - VALUES[position]);
        Log.e("time1=",System.currentTimeMillis()-a+"");
        return result;
    }

}

                                                杏树林研发 倪圣文