Hexagon对数据的操作指令
Hexagon处理器对标量与矢量计算提供了丰富的指令,在本文中,我们就给各位介绍一下Hexagon中各种指令集。
l XTYPE-通用的数据指令
l ALU32-针对32位数据的算术与逻辑运算指令
1.数据类型
Hexagon处理器提供了对如下数据处理的指令:
l 定点数据
l 浮点数据
l 复数数据
l 矢量数据
1.1定点数据的处理
Hexagon处理器提供了对8位,16位,32位或64位的定点数据处理,这些数据既可以是整数型也可以是分数数据,有符号整数或无符号整数格式。
1.2浮点数据的处理
Hexagon处理器提供了对32位浮点数据的处理指令,这些数据应符合IEEE单精度浮点格式。
根据IEEE制定的标准,我们可以定义出表示正数或负数的无限大以及“非数字(NaN这个表示数据没有算术意义)。
浮点数据可以被保存在通用寄存器以内
1.3复数数据的处理
Hexagon处理器提供对32位或64位复数数据的处理。
复数数据包括了有符号的实数部分以及有符号的虚数部分。给定了两个复数数据(a+bi)与(c+di)后,负数的相乘指令将在一个指令内计算实数部分以及虚数部分。
复数可以被打包至一个通用寄存器或寄存器对。打包后,虚数部分在寄存器中将占主要的部分。
1.4矢量数据
Hexagon处理器提供了对64位矢量数据处理的指令
矢量数据类型可以将多种多样的数据类如字节,半字或字打包至64位寄存器,矢量数据指令一般用于视频与图像处理。
八个八位字节可以被打包至一个64位寄存器中,下图显示了矢量字节的处理
向量的字节操作
向量的半字操作
向量的字操作
2Z指令选择
有些指令支持可选的分尺度,饱和系数以及舍入。没有模式位用来控制这些选择,这些选择在指令中被明确的定义了,本部分就将介绍这些选项
2.1分尺度
在分数数据类型中,数据可以被看成由字的长度定义的定点分数值。
分尺度在指令中可以通过:<<标志来表示,例如
R3:2 =cmpy(R0,R1):<<1:sat
当两个分数相乘,商必须改变尺度来保存原始的分数数据格式。Hexagon处理器允许分尺度的操作,这些操作可以移位0或1位。1的移位是针对Q1.15数据而言的,0的移位是针对整数的相乘而言的。
2.2饱和度
对于饱和形式,有几种明确的指令。如果一个饱和算术指令的结果比最小值药效,那么这个结果会被设置为最小值。同样的,如果饱和算术指令的结果比最大值要大,那么结果会被设置为最大值
饱和计算在指令中被定义为:sat标志,例如:
R2 = abs(R!):sat
用户状态寄存器中的OVF位用来表示是否出现饱和。这一位将会被保留知道控制寄存器明确定义。对于矢量类型的饱和操作,如果矢量数据饱和了,那么OVF就会被置位
2.3算术舍入
有符号整数的相乘指令支持算入舍入。算术舍入操作一个双精度并加上0x8000至低16位
舍入操作可以通过使用:rnd来操作:例如
R2 = mpy(R1.h,R2.h):rnd
注意:算术舍入将会积累数值误差,特别是当数值刚好是0.5的时候,这种情况在被二整除时特别频繁
2.4收敛舍入
为了解决算术舍入的误差问题,Hexagon处理器包括了四个可以支持正数与负数的指令集来实现收敛舍入选项。
这些指令的作用为:
l 分别对(A+B)或者(A-B)做平均以及负平均计算
l 根据结果的最后两个位,通过如下方法加入一个舍入常数
如果LSB位为00,那么加0
如果LSB位为01,那么加0
如果LSB位为10,那么加0
如果LSB位为11,那么加1
l 右移结果一位
2.5对于除法以及开根号分尺度
在Hexagon处理器上,浮点除法以及开根号操作是通过软件库来实现的。为了使这些指令有效率的进行,处理器支持多种乘法累积指令,这些也被称作尺度FMA
尺度FMA支持浮点累加指令的积的尺度变换。
尺度变换在指令中通过添加:scale来表示,以及一个分支寄存器操作数例如
R3 += sfmpy(R0,R1,R2):scale
注意:尺度FMA指令不可在除法以及开根号库的其他路径使用,暂时无法保证Hexagon处理器未来的版本将会实现这些功能。未来的版本将假设尺度FMA只会被用到除法与开根号库
3XTYPE类型指令
XTYPE指令类包括了大多数的数据处理指令,这些指令可以被划分为如下几类
l ALU
l 位计算
l 复数
l 浮点
l 相乘
l 转置
l 分支预测
l 移位
3.1 ALU指令
ALU指令可以更改八位,十六位,三十二位以及六十四位的数据,这些操作包括
l 无饱和的情况下相加与相减
l 无累加的情况下相加与相减
l 绝对值
l 逻辑操作
l 最小值,最大值指令
l 64位数据的寄存器转换
l 字与半字的转换
l 对比
3.2 位运算
位运算指令可以寄存器或寄存器对中的位,这些指令包括了
l 位插入
l 有符号与无符号位的提取
l 比较位的掩码
l 设置/清零/翻转位
l 插入或取出位
l 位翻转
l 分离位域
l 等
3.3 复数操作
复数操作包括
l 复数的加与减
l 复数相乘(可选舍入或打包)
l 向量复数相乘
l 向量复数的共轭,旋转,实数与虚数的相乘
3.4 浮点运算
浮点运算可控制单精度浮点数,这些操作包括加减,相乘,最小值最大值比较,格式转换
Hexagon浮点操作的定义支持IEEE浮点标准。然而,IEEE所要求的操作如相除以及开方不能直接实现。取而代之的,Hexagon处理器中有特殊的寄存器来实现这些操作,这些操作包括了
l 一种特殊版本的熔合乘法累积(在库路径中被特殊设计)
l 倒数或开方的近似(通过计算大概的初值)
l 极端值的辅助(如果输入数无法产生正确的结果,那么将会使用收敛算法来改变输入)
3.5 相乘
相乘操作支持浮点数,包括单精度以及双精度。这些操作数可以来自寄存器的高位或低位,这些取决于指令的要求。16位乘以16位的结果可以选择是否被累加,饱和,舍入或者左移0至1位
相乘指令可以支持有符号乘以有符号,无符号乘以无符号以及有符号乘以无符号
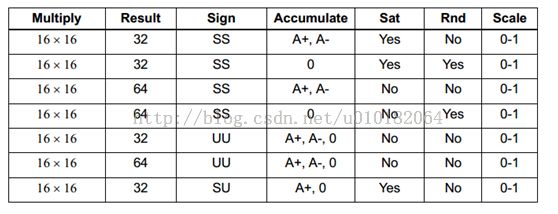
下表总结了16位乘以16位单精度操作的指令
l SS : 实现有符号与有符号数的相乘
l UU : 实现无符号数与无符号数的相乘
l SU :实现有符号数与无符号数的相乘
l A+ : 将结果累加
l A- : 将结果从累加中减去
l 0 : 结果不会被加入到累加中
单精度相乘操作
双精度相乘操作
3.6 移位
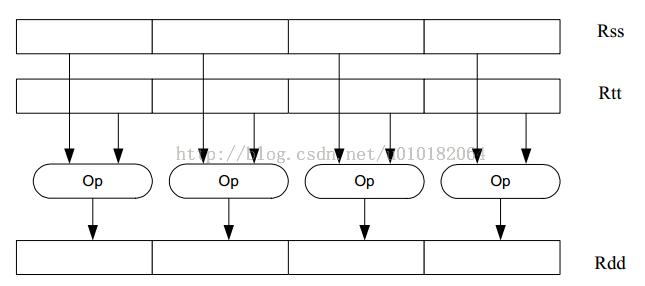
尺度收缩操作可以实现多种多样的32以及64位移位以及选择性的加或减以及逻辑操作,下图显示了一般情况下的操作
64位的移位以及加减逻辑操作
在以寄存器为基地址的操作中,Rt寄存器是一个有符号数,如果这个值为正,那么指令的值表示移位的方向。如果这个值为负,那么移位方向与定义的相反
当算术右移实现时,有符号位被移入,这种操作在逻辑右移实现,逻辑左移也同样适用。
4 向量操作
向量操作可支持字节,半字,字的向量算术运算
向量操作的指令从属于XTYPE指令类(除了向量加,减以及半字均值,这些属于ALU32)
向量的字节操作如下
l 向量的加与减有符号或无符号数
l 向量中无符号字节的最小值与最大值计算
l 向量中的有符号自己的对比,平均值,总和差分运算
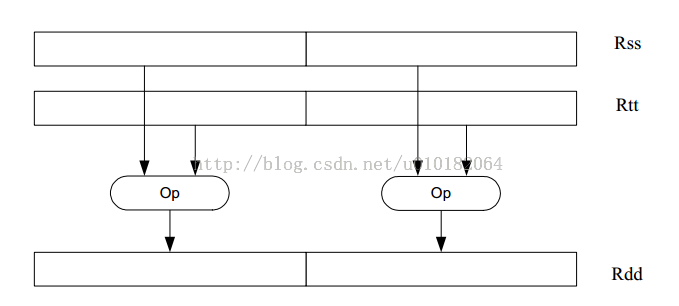
如下图,限制了向量算术左移半字操作,在这个操作中,每个16位的半字右移相同的数目,这些数目在寄存器中被明确定义