选择排序

在介绍选择排序算法前，我们再回顾下冒泡算法。

 

冒泡算法是通过两两比较，不断交换,逐个推进的方式，来进行排序的。

一次遍历，得到一个最值。

 

冒泡算法最费时的是什么？

 

一是两两比较

一是两两交换， 交换要比比较费时多了。

 

在冒泡算法一篇中，介绍了几种改进方法，那几种改进方法为什么放在冒泡算法中一篇中，而不另一一篇介绍？

 

原因就是：无论那几种方法怎么改进，都还是基于两两交换不断推进的冒泡算法。从广义上说，都是属于冒泡算法。

那还有没有其它改进的余地呢？

冒泡算法两两交换的目的是什么？-------找出最值。

 

而通过这种方式取得最值得代价是很大的，因为，每次遍历，可能需要很多次交换才能找到最值，而这些交换都是很浪费时间的。

如果能减少交换次数，同时又能取得最值，那么这就是一种改进。

 

因此问题便转换为：如何求最值？求最值得方法有几种？

 

正所谓条条大路通罗马All RoadsLead to Rome，做成一件事的方法不只一种，人生的路也不只一条。

 

因此，除了使用两两交换的算法找出最值外，或许还有其它方式。

如果有的话，就是通过另外的思路求得最值，于是便跳出了冒泡的思维模式。

 

好了，大家想想有没有其他的方法遍历一次就可求出最值？

求最值，需要比较，但不一定非得通过不断推进的方式。

 

那如何能更好的求得最值呢？

很自然的一种想法便是：

每次遍历，只选择最值元素进行交换，这样一次遍历，只需进行一次交换即可，从而避免了其它无价值的交换操作。

 

如何求得最值元素所在位置呢？

这还得通过遍历比较。

 

具体方法为：

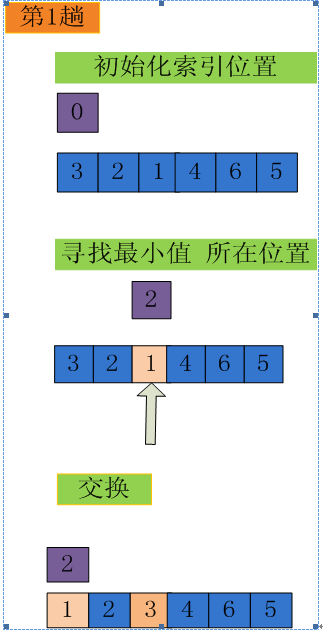
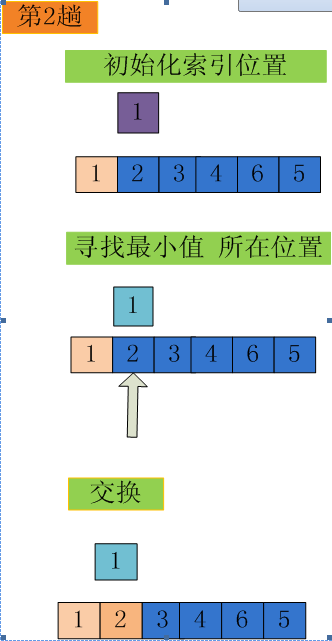
遍历一次，记录下最值元素所在位置，遍历结束后，将此最值元素调整到合适的位置

这样一次遍历，只需一次交换，便可将最值放置到合适位置

 

这便是 简单选择排序算法。

public int[] selectionSort(int[] A, int n) {
        // write code here
        for(int i=0;i<n-1;i++)
        {           
            int index = i;
            for(int j = i+1;j<n;j++)
            {
                if(A[j]<A[index])
                    index = j;
            }
            if(index!=i)
            {
                int tmp = A[index];
                A[index] = A[i];
                A[i] = tmp;
                
            }
        }
        return A;
    }