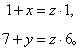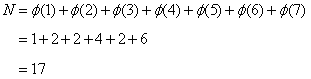farey(法莱）数列 (USACO Ordered Fractions)

载自：  http://blog.csdn.net/bao110908/archive/2007/11/28/1905328.aspx

 

分数有不少有趣的特性，就连普通的分数也有不少有趣的东西。也许你回想得起，算术里头的普通分数是指分母、分子均为整数的那样一种分数。当分母大于分子时，该分数称为真分数。

如果指定一个分母的上限，再把各普通分数（以最简分数形式出现）按从小到大的次序排列，譬如说，当分母不大于 7 时，我们可以得出以下 17 个分数：，这就是所谓的法莱数列。

约翰 ? 法莱（John Farey）是生活在拿破仑时代的一位多才多艺之士。作为土地丈量与勘察人员的他，收集过不少化石与矿物，业余时间他在著名的《哲学杂志》上写了大量科普文章，题材散布之广令人惊讶。他真是一位“杂家”，文章内容涉及地质、音乐、十进制钱币、马车轮盘、彗星，乃至本文要讲的法莱数列。他并不认为这个发现特别重要，更未预料到由于他发现了漏过机敏的费马与欧拉眼睛的一些小东西而使他得以在数学中名垂青史，然而必须遗憾地指出，数学里头一再发生这类事情：享有盛名者并非原始发现人，有个名叫哈罗斯（C. Haros）的人比法莱的发现早 14 年，但大数学家柯西不知道此事，而把功劳归在法莱名下，其他的人则重复了柯西的说法。看来，法莱的运气较好，“法莱数列”发起音来要比“哈罗斯数列”好听一些，也许有某个阿拉伯数学家比哈罗斯的发现还要早上一千年，真是天晓得！

这些事实在 1816 年（约翰 ? 法莱在这一年首次观察到）之前从未有人研究过，这种说法真令人不敢相信。发现是在仔细审阅亨利 ? 戈德温所编的、冗长的小数商表格时作出的。法莱的意外发现马上被当时的数学家们紧紧抓住，不久以后，此种分数的理论即被彻底阐明。其中的部分理论是相当粗浅的，而另一些则比较深奥一些，此种情况，对号称“数学女王”的数论来说，并不鲜见。

在注视上述数列时马上会产生一些问题：
1. 这种分数究竟有多少？其个数能否表示为给定数（例如上例中的分母 7）的函数？
2. 相邻分数之间有何种联系？

只要对数列略瞥一眼（略瞥一眼的话根本是看不出的。——火龙果注），即可回答第二个问题。对相邻的三个分数而言，中间分数的分子是左、右两个分数的分子相加而得，分母也类似。当然所得之结果尚需约分，化成最简分数。例如在上述数列中可任取毗邻的三项，于是得到。循此规则，只要给出数列的前两项，即可推出相继各项。而对前两项来说，如果分母不准超过 7，当然肯定是与，设第三个分数为，于是形成一个三数组。根据上述法则，，当然这不一定意味着 1 + x = 1，7 + y = 6，因为也可通过约分而来，但若 z 为分子、分母的最大公因子，则

从而 x = z - 1，y = 6z - 7。由于 y 不能超过 7，z 只能是 2，于是 x = 1，y = 5，故第三个分数是，对三数组来说，我们有 1 + x = 2z，3 + y = 5z，即 x = 2z - 1，y = 5z - 3，这时 z 的可能值是 1 或 2，而 z = 2 是唯一的正确值。有一个规则可解决模棱两可的迷惑。

设 n 为法莱数列之阶（就上例而言，n = 7），且是数列中相邻的三项，则，这里的 z 是等于或小于的最大整数。显然，等于或小于的最大整数是 2。对三数组的前一例来说，我们有，亦即 z = 2。

在取三数组时，则有，因而 z = 3，于是 5 + x = 3 ? 3，7 + y = 3 ? 4，故得出 x = 4，y = 5，这就求出接在后面的分数了。

阶为 n 的法莱分数的个数可由下法求得：既然所有的分数均为最简分数，对给定分母 b 来说，分子的个数必定是小于 b 且与之互质的诸数之和，即欧拉函数，对从 2 到 n 的一切正整数均可援用此种推理法，因此，阶为 n 的法莱分数的个数 N 应当等于。若 n = 7，我们即有

N 增大时，N 的值随之迅速递增，n = 100 时，N = 3043。由此可知，分子与分母都不超过 100 时，竟有如此之多的既约普通分数。

也许有人想证明法莱数列中相邻三数之间分子、分母所存在的关系以及上述求 z 的规则。这里可以告诉大家，证明并不太容易。

法莱数列的另一性质是：与等距离的两个分数是互补的，其和等于 1，除 x = 1 与 x = 2 外，恒为偶数，因此

恒为奇数，因此法莱数列的项数必定是奇数，而其正中的一项必为。

还有一个性质：相邻两个分数之差一定等于它们的分母乘积之倒数。

全文引自 Albert H. Beiler 著，谈祥伯译：《数论妙趣——数学女王的盛情款待》，上海教育出版社 1998 年版，第 202～205 页，略有改动。