C语言产生满足正态分布的随机数
C语言中可以通过rand函数生成满足均匀分布的随机数,但是生成满足正太分布的随机数就没有那么简单了,下面对常用的几种方法进行总结并用C++编程实现。
方法一:由均匀分布的随机数来产生
一个简单可行的并且容易编程的方法是:求12个在(0,1)上均匀分布的和,然后减6(12的一半)。这种方法可以用在很多应用中,这12个数的和是Irwin-Hall分布;选择一个方差12。但此推导的结果限制在(-6,6)之间,并且密度为12。
方法二:Box-Muller方法
Box-Muller方法是以两组独立的随机数U和V,这两组数在(0,1]上均匀分布,用U和V生成两组独立的标准常态分布随机变量X和Y:
方法三:由正弦曲线图形得到的直观结果
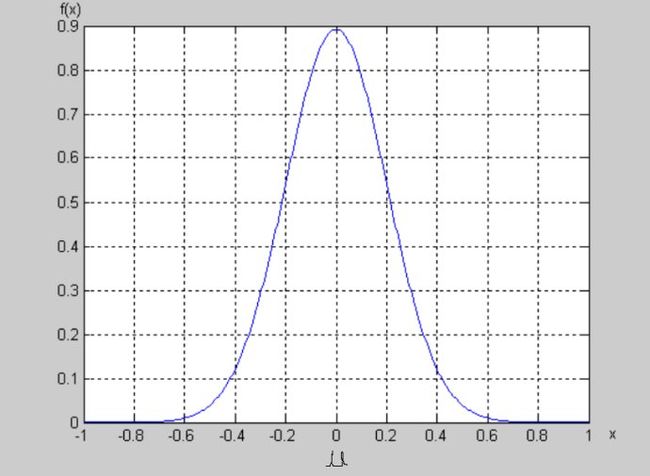
图1 正态分布曲线
从上图可以看出,在μ附近的概率密度大,远离μ的地方概率密度小,我们要产生的随 机数要服从这种分布,就是要使产生的随机数在μ附近的概率要大,远离μ处小。算法的主要思想是:在上图的大矩形中随机产生点,这些点是平均分布的,如果产生的点落在概率密度曲线的下方,则认为产生的点是符合要求的,将它们保留,如果在概率密度曲线的上方, 则认为这些点不合格,将它们去除。如果随机产生了一大批在整个矩形中均匀分布的点,那 么被保留下来的点的横坐标就服从了正态分布。可以设想,由于在μ处的 f(x)的值比较大,理所当然的在μ附近的点个数要多,远离μ处的少,这从面积上就可以看出来。我们要产生的随机数就是这里的横坐标。
根据以上所述三种方法,编写C++测试代码如下:
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include <fstream>
#include <iostream>
using namespace std;
#define pi 3.1415926
#define rd (rand()/(RAND_MAX+1.0))
//区间[min,max]上的均匀分布,min和max要求传入的参数类型一致
template <<span style="color:blue">class T>
T rand(T min, T max)
{
return min+(max-min)*rand()/(RAND_MAX+1.0);
}
//求均值为miu,方差为sigma的正太分布函数在x处的函数值
double normal(double x, double miu,double sigma)
{
return 1.0/sqrt(2*pi)/sigma*exp(-1*(x-miu)*(x-miu)/(2*sigma*sigma));
}
//按照矩形区域在函数值曲线上下位置分布情况得到正太函数x值
double randn(double miu,double sigma, double min ,double max)
{
double x,y,dScope;
do{
x=rand(min,max);
y=normal(x,miu,sigma);
dScope=rand(0.0,normal(miu,miu,sigma));
}while(dScope>y);
return x;
}
double randn(int type)
{
//按照12个均匀分布之和减去6得到正态分布函数的x值
if (type==1)
return rd+rd+rd+rd+rd+rd+rd+rd+rd+rd+rd+rd-6.0;
//按照计算公式y=sqrt(-2*ln(U))*cos(2*PI*V)计算得到x
else if(type==2)
return sqrt(-2*log(rand()/(RAND_MAX+1.0)))*cos(2*pi*rand()/(RAND_MAX+1.0));
else
return randn(0.0,1.0,-10.0,10.0);
}
int main(int argc,char* argv[])
{
srand((unsigned)time( NULL ));
ofstream outfile("321.txt");
for (int i=0;i<100;i++)
{
//randn(1)、randn(2)和randn(3)效果差不多
outfile << randn(3) << endl;
}
return 0;
}
参考:
[1] http://zh.wikipedia.org/wiki/正态分布
[2] http://en.wikipedia.org/wiki/Normal_distribution
[3] http://wenku.baidu.com/view/e9de620d7cd184254b3535c9?pn=2&ssid=&from=&bd_page_type=1&uid=bd_1332071259_725&pu=sl@1,pw@1000,sz@224_220,pd@1,fz@2,lp@0,tpl@color,&