A*启发式搜索基础
A*启发式搜索基础
传统的搜索方式是盲目搜索,即到每一步的时候并没有对每种情况进行有效的区分,这样的结果是浪费了大量的时间,对很多没有必要的数据进行了搜索。
而A*算法则在搜索的过程中会选取认为“最优”的状态进行搜索,而这正是这种算法的精华部分。
其实我们可以将他和Dijkstra进行一定的对比,他们的共同点很多,都是每次选取最优的点开始搜索,但是他们的“最优”策略不同也就决定了不同的效率。
- Dijkstra是每次选取距离“出发点”最近的点开始搜索
- A*算法则是选取距离“目标点”估计值最小的点开始搜索
注意这里的估计值就是A*算法的核心部分了,本博文最后会介绍和Dijkstra的具体效率的区别。
A*算法将点到重点的距离分为两个部分:
F(n)=G(n)+H(n)
介绍:
- F(n) 表示起点到目标的估计距离
- G(n) 表示起点到n点的准确距离
- H(n) 表示n点到目标点的估计距离
我们先假设从 n 点到目标点的准确距离为 H′(n) ,当然 H′(n) 的准确值我们并不知道,否则我们就不用费力气去求了。
这里 H(n) 需要满足的条件是
- H(n)<=H′(n)
需要说明的是,我们A*搜索的核心就是 H(n) 的构建,最后构建的好坏直接决定了我们搜索的效率,我们的好是指: H(n) 越贴近 H′(n) 越好,但是注意一定不能超过实际 H′(n) 的值。
为了和大多数的讲解名字对应,本博文采用相同名字,即名openlist的优先队列来存放需要搜索的内容,具体搜索步骤如下
- 预定义 H(n)=|beginx−endx|+|beginy−endy|
- 预定义 F(n)=G(n)+H(n)
openlist中 F(n) 值小的优先级别高
- 将起点加入openlist中
- 从队列中弹出元素
- 对弹出元素的周边进行搜索,如果发现有未被搜索到的位置,并且不是墙,河水,峡谷等不能行走的位置,则将其加入到队列中,并将其指向弹出元素。
如果发现有已经被搜索过的位置,则查看其 F(n) 值是否比现在走到那个位置的 F(n) 值小,若现在是更优解,则更新其 F(n) 值。如果其不在队列中则把其重新加入队列,否则什么也不用做。- 重复2-4步,直到找到目标点
- 最小路径即目标点的 F(n) 的值,同时根据维护的指针就可把最优路径推出来
补充:
我们从 F(n)=G(n)+H(n) 中可以推导出
- 当 G(n)=0 时,算法相当与bfs;
- 当 H(n)=0 时,算法相当于dfs;
自己写了一个示例代码如下:
@Frosero
#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define INF 0x3f3f3f3f
using namespace std;
char mps[12][21] = { //x*
{"...................."}, //0
{"...S................"}, //1
{"...................."}, //2
{"...................."}, //3
{"....##########......"}, //4
{"...................."}, //5
{"...................."}, //6
{"...................."}, //7
{".............#......"}, //8
{".............#..P..."}, //9
{".............#......"}, //10
{"...................."}, //11
}; //原地图
const int beginx = 1,beginy = 3,endx = 9,endy = 16;
int link[12][21] = {0}; //1-up 2-right 3-down 4-left
int dx[] = {1,-1,0,0},dy[] = {0,0,1,-1},f[12][21]; //f用于储存F值
bool can_move(int x,int y){
return x >= 0 && x < 12 && y >= 0 && y < 20 && mps[x][y] != '#';
}
class Node{
public:
int x,y;
int f,g,h;
Node() = default;
Node(int X,int Y,int G):x(X),y(Y),g(G) {
this->h = abs(x - endx) + abs(y - endy) ; //计算H(n)
this->f = this->g + this->h;
}
bool operator < (const Node &rhs) const {
return this->f > rhs.f;
}
};
void A_bfs(){
for(int i=0;i<12;i++) for(int j=0;j<21;j++) f[i][j] = INF;
priority_queue<Node> openlist;
while(!openlist.empty()) openlist.pop();
openlist.push(Node(beginx,beginy,0));
f[beginx][beginy] = abs(beginx - endx) + abs(beginy - endy) ;
while(!openlist.empty()){
Node now = openlist.top(); openlist.pop();
if(now.x == endx && now.y == endy) break;
if(now.f > f[now.x][now.y]) continue; //如果发现刚才记录的F值比现在实际F值小
//说明该点已经被更新过,忽略即可
for(int i=0;i<4;i++){
int nx = now.x + dx[i];
int ny = now.y + dy[i];
if(can_move(nx,ny) && now.g + 1 + abs(nx - endx) + abs(ny - endy) < f[nx][ny]){
mps[nx][ny] = mps[nx][ny] == 'P' ? 'P' : '*' ;
f[nx][ny] = now.g + 1 + abs(nx - endx) + abs(ny - endy) ;
if(nx == now.x + 1) link[nx][ny] = 1;
else if(nx == now.x - 1) link[nx][ny] = 3;
else if(ny == now.y + 1) link[nx][ny] = 4;
else if(ny == now.y - 1) link[nx][ny] = 2; //标记指针数组
openlist.push(Node(nx,ny,now.g + 1));
}
}
}
}
int main(){
A_bfs();
int x = endx,y = endy;
while(1){
if(link[x][y] == 1) x--;
else if(link[x][y] == 2) y++;
else if(link[x][y] == 3) x++;
else if(link[x][y] == 4) y--;
if(x == beginx && y == beginy) break;
mps[x][y] = '+';
}
printf("ans is : %d\n",f[endx][endy]);
for(int i=0;i<12;i++,printf("\n")){
for(int j=0;j<20;j++) printf("%c",mps[i][j]);
}
return 0;
}
/* 输出: ans is : 21 ...*****............ ..*S************.... ..*+*************... ..*+************.... ..*+##########***... ..*+++++++++++++**.. ..*************+**.. ...************+**.. ....*********#*+**.. .....********#*+P... ......*.*...*#.*.... .................... 符号解释 S:起点 P:目标点 *:搜索过的路径 +:搜索过的最优路径 #:墙 Process returned 0 (0x0) execution time : 0.362 s Press any key to continue. */
作为比较,我们用Dijkstra再做一次结果:
@Frosero
#include <iostream>
#include <queue>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define INF 0x3f3f3f3f
using namespace std;
char mps[12][21] = { //x*
{"...................."}, //0
{"...S................"}, //1
{"...................."}, //2
{"...................."}, //3
{"....##########......"}, //4
{"...................."}, //5
{"...................."}, //6
{"...................."}, //7
{".............#......"}, //8
{".............#..P..."}, //9
{".............#......"}, //10
{"...................."}, //11
};
const int beginx = 1,beginy = 3,endx = 9,endy = 16;
int link[12][21] = {0}; //1-up 2-right 3-down 4-left
int dx[] = {1,-1,0,0},dy[] = {0,0,1,-1},f[12][21];
bool can_move(int x,int y){
return x >= 0 && x < 12 && y >= 0 && y < 20 && mps[x][y] != '#';
}
class Node{
public:
int x,y;
int g;
Node() = default;
Node(int X,int Y,int G):x(X),y(Y),g(G) { }
bool operator < (const Node &rhs) const {
return this->g > rhs.g;
}
};
void A_bfs(){
for(int i=0;i<12;i++) for(int j=0;j<21;j++) f[i][j] = INF;
priority_queue<Node> openlist;
while(!openlist.empty()) openlist.pop();
openlist.push(Node(beginx,beginy,0));
f[beginx][beginy] = 0 ;
while(!openlist.empty()){
Node now = openlist.top(); openlist.pop();
if(now.x == endx && now.y == endy) break;
for(int i=0;i<4;i++){
int nx = now.x + dx[i];
int ny = now.y + dy[i];
if(can_move(nx,ny) && now.g + 1 < f[nx][ny]){
mps[nx][ny] = mps[nx][ny] == 'P' ? 'P' : '*' ;
f[nx][ny] = now.g + 1;
if(nx == now.x + 1) link[nx][ny] = 1;
else if(nx == now.x - 1) link[nx][ny] = 3;
else if(ny == now.y + 1) link[nx][ny] = 4;
else if(ny == now.y - 1) link[nx][ny] = 2;
openlist.push(Node(nx,ny,now.g + 1));
}
}
}
}
int main(){
A_bfs();
int x = endx,y = endy;
while(1){
if(link[x][y] == 1) x--;
else if(link[x][y] == 2) y++;
else if(link[x][y] == 3) x++;
else if(link[x][y] == 4) y--;
if(x == beginx && y == beginy) break;
mps[x][y] = '+';
}
printf("ans is : %d\n",f[endx][endy]);
for(int i=0;i<12;i++,printf("\n")){
for(int j=0;j<20;j++) printf("%c",mps[i][j]);
}
return 0;
}
/* 输出: ans is : 21 ******************** ***S++++++++++****** *************+****** *************++***** ****##########+***** **************+***** **************+***** **************+***** *************#+****. *************#++P... *************#**.... ***************..... 符号解释 S:起点 P:目标点 *:搜索过的路径 +:搜索过的最优路径 #:墙 Process returned 0 (0x0) execution time : 0.362 s Press any key to continue. */
通过比较我们可以很轻松的发现A*搜索相比于Dijkstra的优越性
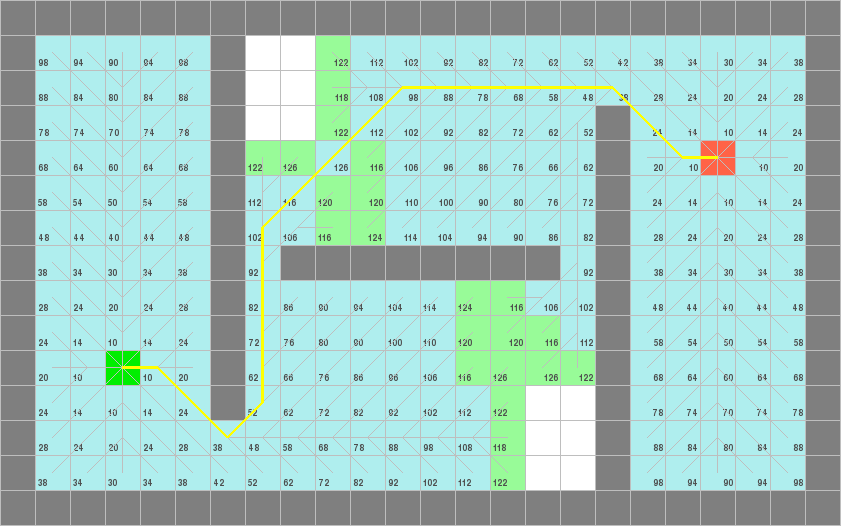
下面是在网上找的几组图片来进行一些对比
图片来源:[http://blog.csdn.net/luckyxiaoqiang/article/details/6996963]
例一
1. A*(曼哈顿距离)
2. A*(欧氏距离)
3. A*(切比雪夫距离)
4. Dijkstra

5. 双向BFS
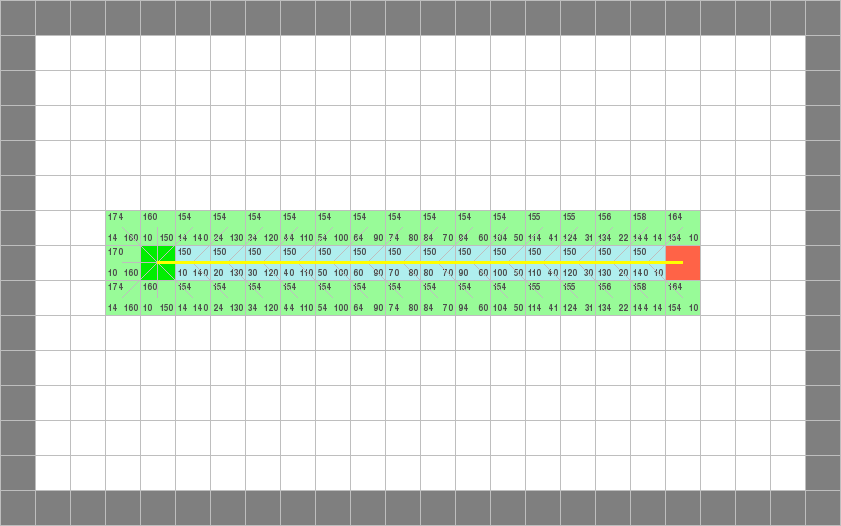
例二
1. A*(曼哈顿距离)
2. A*(欧氏距离)

3. A*(切比雪夫距离)

4. Dijkstra
5. 双向BFS
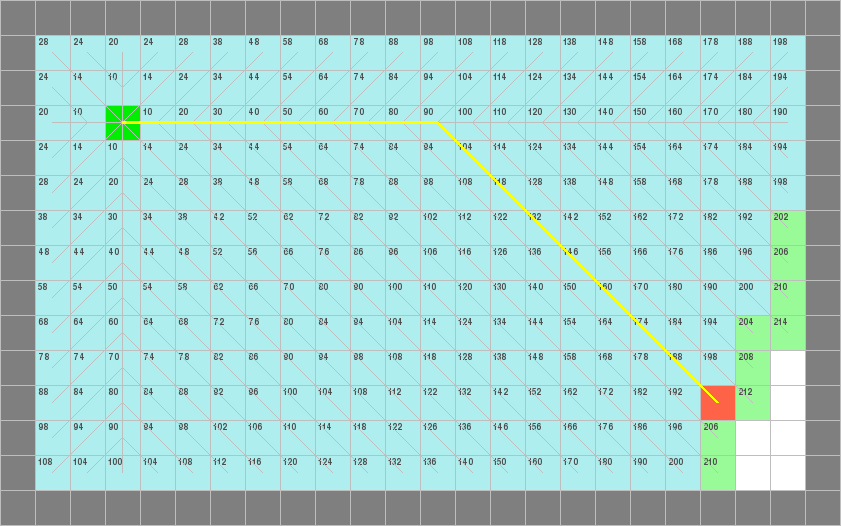
例三
1. A*(曼哈顿距离)
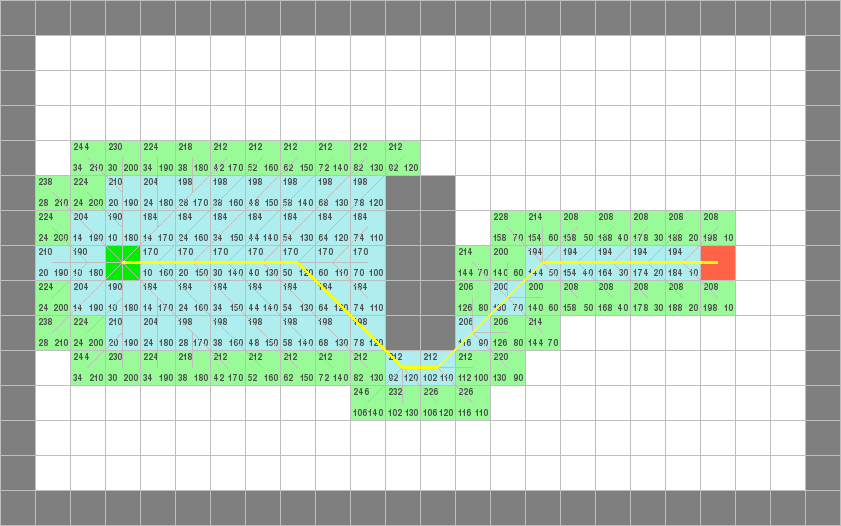
2. A*(欧氏距离)
3. A*(切比雪夫距离)

4. Dijkstra

5. 双向BFS

例四