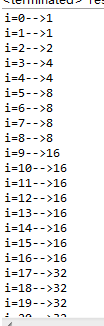Java进阶之----HashMap源码分析
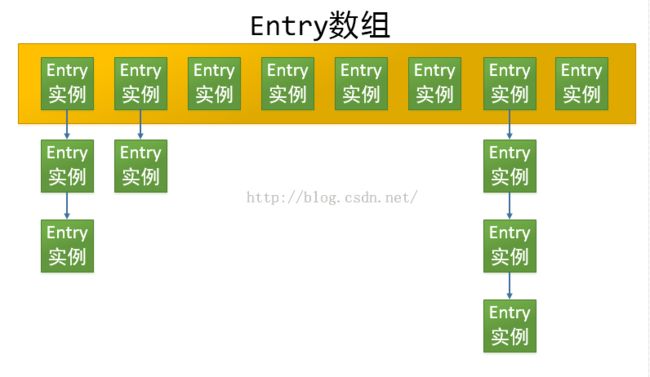
今天我们接着来看HashMap的源码,对几个常用的方法进行分析。在分析之前,我们还是要先对HashMap的结构有一个了解。看过之前我分析的ArrayList和LinkedList源码的朋友应该清楚,ArrayList内部是以数组实现的,LinkedList内部是以链表实现的。而HashMap则是对数组和链表的结合,虽然看上去复杂了一些,不过仔细分析一下,还是很好理解的。我们来看一张图片,是我根据我的理解画的。
我们在来看看Entry的内部结构是什么:
以上两个图,相信大家对HashMap的结构有一个大致的了解了,在真正看代码之前,我先来介绍一下基本知识。从第一个图可以看出来,有的数组元素里连接着另一个Entry实例,有的只有一个,为什么会这样呢?是因为相同的key经过hash计算后,被分配到了相同的位置。为什么会出现这样的结果呢?是因为出现了hash冲突,即在一个较小的空间里存放较多的数据,必然会有一部分数据没有地方存放,那么这多出来的数据,就要挂在已存在的元素的下方,形成链表结构。以此来解决hash冲突。
下边我们跟着代码,来看看HashMap的具体实现。
内部使用的变量
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // 默认的Entry数组的初始化大小,默认为16
static final int MAXIMUM_CAPACITY = 1 << 30; // 最大的Entry数组大小
static final float DEFAULT_LOAD_FACTOR = 0.75f; // 负载因子,默认0.75,它的作用在下边我进行说明
static final Entry<?,?>[] EMPTY_TABLE = {}; // 空的Entry数组
transient Entry<K,V>[] table = (Entry<K,V>[]) EMPTY_TABLE;
transient int size; // HashMap中元素的个数
int threshold; // 临界值,<span style="font-family:Arial, Helvetica, sans-serif;">threshold = 负载因子 * 当前数组容量,实际个数超过临界值时,会进行扩容</span>
final float loadFactor; // 负载因子
transient int modCount; // 更改次数
这里说明一下负载因子,负载因子,我们可以理解为空间的填满程度。
1、负载因子越大,填满的元素越多,空间利用率增加,hash冲突的机会增加,每个元素下挂载的链表会越来越长,同时会导致查找元素的效率变得低下。
2、负载因子越小,填满的元素越少,空间利用率降低,hash冲突减少,但是数组中的元素过于稀疏,导致数组中很多空间还没有用就开始扩容,不过好处是查找的元素的效率相对高一些。
所以,必然要在“查找效率”和“空间利用率”之中做一个折中,让它们处在一个相对的平衡状态。0.75就是这样的一个相对平衡的状态。
HashMap源码分析
构造方法分析
public HashMap(int initialCapacity, float loadFactor) {
if (initialCapacity < 0)
throw new IllegalArgumentException("Illegal initial capacity: " +
initialCapacity);
if (initialCapacity > MAXIMUM_CAPACITY)
initialCapacity = MAXIMUM_CAPACITY;
if (loadFactor <= 0 || Float.isNaN(loadFactor))
throw new IllegalArgumentException("Illegal load factor: " +
loadFactor);
this.loadFactor = loadFactor;
threshold = initialCapacity;
init();
}
public HashMap(int initialCapacity) {
this(initialCapacity, DEFAULT_LOAD_FACTOR);
}
public HashMap() {
this(DEFAULT_INITIAL_CAPACITY, DEFAULT_LOAD_FACTOR);
}
public HashMap(Map<? extends K, ? extends V> m) {
this(Math.max((int) (m.size() / DEFAULT_LOAD_FACTOR) + 1,
DEFAULT_INITIAL_CAPACITY), DEFAULT_LOAD_FACTOR);
inflateTable(threshold);
putAllForCreate(m);
}我们可以看到,一共有4个构造方法,前3个都很简单,只是简单的赋值,并没有其他操作。
我们来看最后一个构造方法,跟进inflateTable方法
private void inflateTable(int toSize) {
// Find a power of 2 >= toSize
int capacity = roundUpToPowerOf2(toSize);
threshold = (int) Math.min(capacity * loadFactor, MAXIMUM_CAPACITY + 1);
table = new Entry[capacity];
initHashSeedAsNeeded(capacity);
}可以看到,操作就是初始化Entry数组,在确定数组大小之前,还做了一个操作,我们来看看到底做了什么。
private static int roundUpToPowerOf2(int number) {
return number >= MAXIMUM_CAPACITY
? MAXIMUM_CAPACITY
: (number > 1) ? Integer.highestOneBit((number - 1) << 1) : 1;
}可能是我的水平不高,我对Java的位操作并不是很感冒,看到上边的代码,我完全不知道是在干嘛,没关系,我们写一个测试代码,看看他到底是干嘛的。
final int MAXIMUM_CAPACITY = 1 << 30;
@Test
public void test() {
for (int i = 0; i < 100; i++) {
System.out.println("i=" + i + "-->" + (i >= MAXIMUM_CAPACITY ? MAXIMUM_CAPACITY : (i > 1) ? Integer.highestOneBit((i - 1) << 1) : 1));
}
}测试代码很简单,我们来看看结果
看出来了吧?这段代码的作用是找到大于给定数字的2的n次方的数。。(我表述不太清楚。。表达能力有待提高啊)
找到这个数之后,将它作为初始化的数组大小,为什么是2的N次方,一会儿在解释。。
上边就是构造方法,其实其实就是做了初始化数组,赋值等工作,没有其他的。
put方法分析
public V put(K key, V value) {
// 若为第一次put,则先初始化数组
if (table == EMPTY_TABLE) {
inflateTable(threshold);
}
// key为null,防在table[0]即数组第一个的位置
if (key == null)
return putForNullKey(value);
// 根据key计算hash值,具体计算hash的算法我不太懂,还望有前辈能指点一下
int hash = hash(key);
// 根据hash值和表的长度,确定这个元素存放在数组的第几个位置,即求得元素在数组中的位置的索引值
int i = indexFor(hash, table.length);
// 遍历该位置的链表,如果有重复的key,则将value覆盖
for (Entry<K,V> e = table[i]; e != null; e = e.next) {
Object k;
if (e.hash == hash && ((k = e.key) == key || key.equals(k))) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
// 修改次数+1
modCount++;
// 将新加入的数据挂载到table[i]的位置
addEntry(hash, key, value, i);
return null;
}
我们来看看代码,putForNullKey方法,存储key为null方法,实质上与其他的值没有太大差别,区别是key为null的hashCode为0,所以他总是存储在table[0]的位置。
private V putForNullKey(V value) {
for (Entry<K,V> e = table[0]; e != null; e = e.next) {
if (e.key == null) {
V oldValue = e.value;
e.value = value;
e.recordAccess(this);
return oldValue;
}
}
modCount++;
addEntry(0, null, value, 0);
return null;
}
之后是根据key求得hashCode,不过里边的算法看不太懂,看过几篇文章,但是讲述的不是很明白,不过我们知道它的作用是计算hashCode的即可
final int hash(Object k) {
int h = hashSeed;
if (0 != h && k instanceof String) {
return sun.misc.Hashing.stringHash32((String) k);
}
h ^= k.hashCode();
// 一系列位操作,不太明白要干什么,大致作用就是让元素在数组里分布的均匀一些
h ^= (h >>> 20) ^ (h >>> 12);
return h ^ (h >>> 7) ^ (h >>> 4);
}之后就是根据hashCode和数组的长度,返回元素存储的索引位置
static int indexFor(int h, int length) {
return h & (length-1);
}这块就能印证之前数组长度为什么要为2的N次方了。我们来分析一下
首先,若数组长度为2的N次方,则数组的长度必然为偶数,则,偶数-1必然为奇数,在2进制的表示中,奇数的最后一位为1,所以,与奇数做“&”操作,最后的结果可能为奇数,也可能为偶数。
其次,若数组长度不为偶数,则奇数-1为偶数,偶数在2进制中最后一位为0,那么与偶数做“&”操作,最后的结果只可能是偶数,不可能为奇数,所以在奇数位置的空间不会存储到元素,所以会有二分之一的空间被浪费掉。
综上所述,数组长度取2的N次方,目的是为了能让元素均匀的分布在数组中,减小发生冲突的机会。
得到存储的位置之后, 在数组中的该位置判断是否有值,没有的话就新增一个节点,挂载到数组这个位置的链表上,如果有值的话,则需要遍历当前链表,查看是否有重复的key,若有重复的key,则覆盖对应的value。若与已存在的链表的key不重复的话,则新增节点。
void addEntry(int hash, K key, V value, int bucketIndex) {
// 判断数组是否需要扩容
if ((size >= threshold) && (null != table[bucketIndex])) {
resize(2 * table.length);
hash = (null != key) ? hash(key) : 0;
bucketIndex = indexFor(hash, table.length);
}
createEntry(hash, key, value, bucketIndex);
}
void createEntry(int hash, K key, V value, int bucketIndex) {
Entry<K,V> e = table[bucketIndex];
table[bucketIndex] = new Entry<>(hash, key, value, e);
size++;
}
首先在新增元素前先判断是否需要扩容,我们先讨论不需要扩容的情况。
1、先将数组该位置的链表取出,然后新建Entry对象,将新建的Entry对象的next指向刚刚取出的已存在的链表
如图所示
如图所示
我们再来看看需要扩容的情况,当现有的元素个数大于等于临界值的时候需要进行扩容,跟进resize方法
void resize(int newCapacity) {
Entry[] oldTable = table;
int oldCapacity = oldTable.length;
if (oldCapacity == MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return;
}
Entry[] newTable = new Entry[newCapacity];
transfer(newTable, initHashSeedAsNeeded(newCapacity));
table = newTable;
threshold = (int)Math.min(newCapacity * loadFactor, MAXIMUM_CAPACITY + 1);
}
void transfer(Entry[] newTable, boolean rehash) {
int newCapacity = newTable.length;
for (Entry<K,V> e : table) {
while(null != e) {
Entry<K,V> next = e.next;
if (rehash) {
e.hash = null == e.key ? 0 : hash(e.key);
}
int i = indexFor(e.hash, newCapacity);
e.next = newTable[i];
newTable[i] = e;
e = next;
}
}
}
重点在transfer方法中,这也是HashMap不保证存放元素顺序的根源。实质上是新初始化了一个Entry数组,之后再次遍历之前的Entry数组,根据它们的hashCode重新计算他们在新数组的存放位置。在重新分配之后,原有的元素位置一定会发生改变,所以HashMap不会保证元素的存入取出顺序。
以上就是对put方法的分析。总结起来就是,
使用key计算得到hashCode,之后得到该元素在数组中的存放位置,然后将其放入链表的头部,放入的过程中要对容量进行判断。
get方法分析
get方法相对来说就简单了许多
public V get(Object key) {
if (key == null)
return getForNullKey();
Entry<K,V> entry = getEntry(key);
return null == entry ? null : entry.getValue();
}
final Entry<K,V> getEntry(Object key) {
if (size == 0) {
return null;
}
int hash = (key == null) ? 0 : hash(key);
for (Entry<K,V> e = table[indexFor(hash, table.length)];
e != null;
e = e.next) {
Object k;
if (e.hash == hash &&
((k = e.key) == key || (key != null && key.equals(k))))
return e;
}
return null;
}其实原理就是得到位置索引,遍历链表。其余的就是一些条件判断,相对还是很好理解的。
我们经常使用的几种方法中,大致上都是这样的一个套路,理解了它的数据结构之后,在结合代码研究,还是很好理解的。