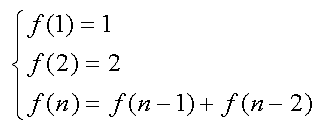（1.1.7.1）上台阶、硬币问题的算法

问题

刚才在首页看到一篇博客，说的是腾讯的一道面试题：一个楼梯有50个台阶，每一步可以走一个台阶，也可以走两个台阶，请问走完这个楼梯共有多少种方法？博主把这题分析的很麻烦。引来很多人围观。我以前也碰到过这个问题。写出来和大家分享一下。

举个例子，假设有3个台阶，则有三种走法：分别是，1-1-1, 1-2, 2-1。

分析

很简单的一道题，学过组合数学的人很快就能想到，这是一个递推关系。假设走完k个台阶有f(k)种走法。

• k = 1时，f(k) = 1
• k = 2时，f(k) = 2
• k = n时，第一步走一个台阶，剩n-1个台阶，有f(n - 1)种走法。第一步走两个台阶，剩n-2个台阶，有f(n - 2)种走法。所以共有f(n - 1) + f(n - 2)种走法。

于是有如下公式

代码

//递归算法

int count(unsigned int n)
{
    if(n == 1)
        return 1 ;
    if(n == 2)
        return 2 ;
    else 
        return count(n - 1) + count(n - 2) ;
}

//非递归算法

int count(unsigned int n)
{
 int a = 1;
 int b = 2;
 if (n == 1)
 {
 return a;
 }
 if (n == 2)
 {
 return b;
 }


 int ret = 0;
 for(int i = 2; i<n; i++)
 {
 ret = a + b;
 a = b;
 b = ret;
 }
 return b;//return ret也是可以的,看你怎么理解
}

具体是怎么走的呢？

上面只给出了有多少种走法，那么具体每一种走法是怎么走的呢？比如n=4时，五种走法分别如下：

1,1,1,1

1,1,2

1,2,1

2,1,1

2,2

我们用一个整型数组来存放每一步的内容，1表示这步走了一个台阶，2表示这步走了两个台阶。回溯法搞定。代码如下。

void count(int n, int t)
{
    if(n < 0)
        return ;
    if (n == 0)
        Output(step, t) ;
    else
    {
        for (int i = 1; i <= 2; ++i)
        {
            step[t] = i ;
            count(n - i, t + 1) ;
        }
    }
}

类似的问题

与此题类似的问题有很多，比如铺地砖问题，自然数拆分等。

铺地砖问题

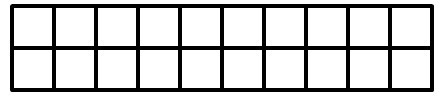
有一个长度为n,宽度为2的地面，有若干块长为2,宽为1的地砖，请问用此地砖铺完这个地面共有多少种方法？

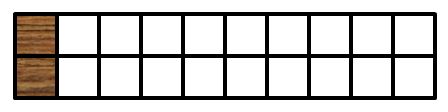
分析一下，假设铺完长度为n的地面有f(n)种方法，如果第一块地砖竖起来铺，还剩下长度为n-1的地面，有f(n-1)种方法。如下图。

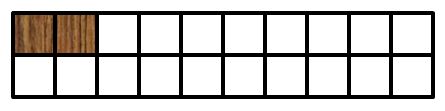
如果第一块地转横着铺，那么还剩下长度为n-2的地面，有f(n-2)种铺法。如下图。

所以这道题与上面的题解法完全一样。不同的题目，相同的模型而已。

自然数拆分

给定一个自然数n，将其拆分为若干个自然数字之和，请问有多少种方法？举个例子，n=4时，可以拆分为1-1-1-1，1-1-2，1-3，2-2。

这题和上面的题很像，不过上面的问题是排列问题，而这题是组合问题，比如n=4时，1-1-2，1-2-1，2-1-1这三种只能算一个拆分。在上面的基础上，去掉重复的组合即可。

1、走台阶问题——一次可以走1,2,3级台阶，N级台阶，共有多少种走法？

     看过了hulu笔试题中关于卡特兰数的应用，我们应该很清楚，对于复杂问题简单化的思路： 关键是把原问题分解成不相交的子问题的并集。

     这里，我们仍然采用这样的思路，第一步走1级，剩下N-1级台阶，第一步走2级，剩下N-2级台阶，第一步走3级，剩下N-3级台阶。故有：f（N）  =  f（N-1） + f(N-2) + f(N-3),且f(2) = 2， f(1) = 1, f(0)=1.

因此，求共有多少种，只需要仿照Fibonacci Sequence数组的求法即可。注意：有递归和非递归两种方法，非递归不会的默默的学去吧。

     另外，如果需要求出具体的策略，如何做？回溯法！又一次让人想起了hulu笔试题中的八皇后问题。回溯法的本质，就是穷举。

回溯法在实现过程中，往往需要维护一个记录路线（策略）的数组，并把每一次的回溯策略记录在此种，当发现到达目标后（如：此处为N级台阶走完），输出结果，否则继续探寻下一个位置（如：此处为下一个台阶）。

     走台阶类似的问题，参看： http://blog.csdn.net/weiqubo/article/details/6880128，铺地砖问题（简单），自然数拆分问题（这个是个组合问题，而走台阶是个排列问题）。

1分2分5分的硬币，组成1角，共有多少种组合

我把比较经典的解法整理出来，一般的for循环解法有空在整理

思路分析： 设1分个数为x，2分个数为y，5分的硬币个数为z，则1*x+2*y+5*z=10； 5*z=10-x-2*y；即： z x对应可能的取值 z=0 时x=10 8 6 4 2 0（6个） z=1 时x=5 3 1（3个） z=2时x= 0（1个） 总共个数为6+3+1=10. 因此，按照规律，本题目组合总数为10以内的偶数+5以内的奇数+0以内的偶数 某个偶数m以内的偶数个数（包括0）可以表示为m/2+1=(m+2)/2 某个奇数m以内的奇数个数也可以表示为(m+2)/2 所以，求总的组合次数可以编程为： number=0; for (int m=0;m<=10;m+=5) { number+=(m+2)/2; } cout<<number<<endl; 这样程序是不是简单多了（只需要累加3次，而上面的3层循环呢？大家自己想想）。别人考你肯定不是考你会不会编这个程序，是考你如何去使程序的复杂度降低。

C语言代码：

#include <stdio.h>
void main(void) {
 int number=0,m;
 // 因为5*z=10-x-2*y<=10；z的取值范围为0、1、2(注意5*z)，所以m的步长是5啊
 for (m=0;m<=10;m+=5) {
  number += (m+2)/2;
 }
 printf("组合数的个数为：%d\n",number);
}

 

该算法对本题没问题，能否提炼出通用算法。
如果6分、4分、2分组成100分怎么处理呢？

和先前一样的道理，2分为x，4分为y，6分为z。则6*z=100-2*x-4*y，可化简为：
3*z=50-x-2*y
z可能的取值为0、1、2···16，
当z=0时，x可以为50 48 46···2 0（26个）
当z=1时，x可以为47 45 43···3 1（24个）
当z=2时，x可以为44 42 40···2 0（23个）
当z=3时，x可以为41 39 37···3 1（21个）
·
·
·
当z=15时，x可以为5 3 1（3个）
当z=16时，x可以为2 0（2个）

因此，按照规律，本题目组合总数为50以内的偶数+47以内的奇数+44以内的偶数+···+5以内的奇数+2以内的偶数
某个偶数m以内的偶数个数（包括0）可以表示为m/2+1=(m+2)/2
某个奇数m以内的奇数个数也可以表示为(m+2)/2

所以，求总的组合次数可以编程为：
number=0;
for (int m=0;m<=50;m+=3)
{
number+=(m+2)/2;
}
cout<<number<<endl;

是不是可以看出规律了呢？实际上就是看表达式（这里是3*z=50-x-2*y），就是把最大乘数（这里是3）放在一边，这也是m增加的步长。而m的最大取值也就是表达式中的这个常数。