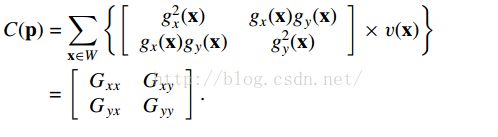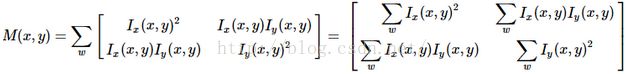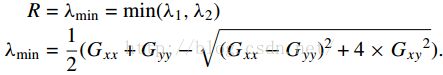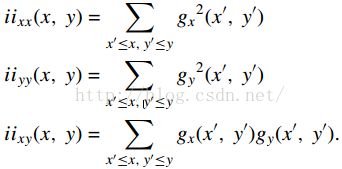基于图像像素梯度的角点检测方法综述

通过图像像素强度的梯度值来确定角点的位置，是非常直观的角点检测方法，下面我们将给出一个基于图像梯度（导数）方法的简介，在这类方法里用的比较多的便是Harris和KLT（Shi-Tomasi）方法了，我们将介绍其原理比较其不同，另外本文还提到了一些早期梯度检测方法（如DET）。

 

一、早期的梯度角点检测方法

DET角点检测子是由Beaudet在1978年提出的，首先定义了一个旋转不变的DET算子：

DET也可以被视为像素点的Hessian矩阵的行列式：

而同高斯曲度也有联系，两者有相同符号。

它主要是基于以下两点：

（1）角点的精确位置一般都是在拉布拉斯变换后图像的尺度空间的过零位置（角点具有一定的尺度不变性，其位置不会随着高斯模糊的扩大而改变）

（2）在靠近角点的位置，DET将会有一个局部的极大值，而这个位置将会在尺度空间直线移动，但这个移动的轨迹却实际是位于角点的角平分线上，即所以尺度上的局部极值都位于这条线上，因此我们可以先根据不同尺度下的两个局部极值，计算连接这两个点的直线，然后找到这条直线上拉布拉斯变换后图像的第一个过零点，就能得到精确的角点位置了。

其算法的步骤：

（1）计算全局图像的拉布拉斯变换

（2）然后在两个或以上的尺度下计算DET，并找到局部的最大值，对于第一个尺度里的局部极值，在第二个尺度里找到对应的极值（这里可以建立一个窗口来寻找最相似的位置）。一旦找到，计算过这两点的直线，然后找到这条直线上，拉布拉斯图像的过零点位置即为角点

除了是基于DET检测子外，上面的高斯曲线也可以作为衡量局部极值点方法

（以上算法，可以参考文章On Corner and Vertex Detection）

还有一种方法是将图像像素考虑为电子，而将梯度考虑为电流，这样我们就可以计算整个图像的磁矢量势场，然后矢量势场的波峰和波谷位置即是角点，如下图所示：

（以上算法，可以参考文章Corner detection via topographic analysis of vector-potential）

 

二、基于SSD的角点检测方法

特征可以被定义为在各方向拥有较小的自相似度的点，而自相似度可以通过SSD（Local sum of squared differences）来衡量，SSD如下公式，也可被视为二阶累积梯度矩阵。这类 最为常见的就是Harris、KLT角点检测方法了。而这些方法的本质上都非常类似，都是利用像素点窗口内的二阶累积梯度矩阵来确定角点响应程度的。

上图给出了二阶累加梯度矩阵的公式，这里的g_x和g_y指像素点在x,y方向上的梯度，而W指以要计算的点为中心的窗口，v指的是权值，将窗口内所有的像素梯度平方及乘积按权值累加便得到了二阶累积梯度矩阵。下面我们将会介绍下这些角点检测方法（Harris同KLT）有什么样的不同，现在又有了什么样的改进。

 （1）思路不一样

这里需要指出不同的是，Harris同KLT推出这个公式的思路不同。Harris角点检测主要是考虑到人眼对角点的识别通常是在一个局部的小区域或小窗口完成的。如果是在角点位置上的窗口，那么其在各个方向上移动，都会使区域内灰度发生了较大的变化。如果只在一个方向上移动时发生较大变化，那么这点需要是在直线上；如果在各个方向上移动都没有发生变化，那么窗口可能位于平滑的区域，图像块相似性公式如下：

而这里的M矩阵就是上面的二阶累积梯度矩阵：

而如果是角点，那么这个M矩阵必须有两个较大的特征值（即指两个较大的变化方向）。

 而KLT方法却是基于光流法思想的，它认为一个好的角点应该是能满足特定算法需要的（即光流法），所以它认为，光流法是通过先在前后两帧图像里分别建立一个固定大小窗口，然后找到让两个窗口间像素强度差的平方和最小的位移。但是如何去选择这样的窗口位置呢？我们知道如果只知道x方向上的分量，而不确定y方向上的分量，会带来孔径效应，即无法确定窗口内移动的具体向量，所以KLT认为好的特征点应该在移动时能同时具有x,y方向上的位移分量。

然后KLT方法从让两个窗口间像素强度差的平方和最小的位移出发，得出如下公式，这里I指当前帧，而J指移动后一帧

上式求导取0得到最小位移值d的公式：

（及）

要想让位移值d具有较大的x,y分量，以避免孔径效应，则需要让G（即上面二阶累积梯度矩阵M）具有两个较大的特征值。

（关于Harris及KLT比较详细的内容，可以参考我的博客及我上传资源内的英文原文）

（2）计算角响应程度公式不一样

Harris主要是通过累积梯度矩阵的两个特征值的比来确定角响应程度，如果比值接近1，说明特征值接近，即此位置有两个不同方向的变化位置，直接求出特征值太复杂，Harris给出了简化的公式：

而KLT方法（也即Shi-Tomasi方法）则是只通过最小特征值来确定，因为如果最小特征值大的话，说明最大特征值也大，也能说明此位置有两个较大的变化方向。最小特征值的计算可以根据如下公式来获得：

这里还要提下Shi-Tomasi方法，Shi-Tomasi方法是KLT方法的一个改进（或完善），其对KLT的改进主要在于引进了图像块匹配时仿射不变性，即在上述KLT算法里g向量里再加了仿射矩阵的四个参数（此时g有6个元素），不过对于单张图像的角点检测问题，这个并不重要。其主要是角点跟踪过程中，提高匹配的精确度，及时删除一些不匹配的特征点，而在计算位移时，并不利用仿射矩阵，而同KLT的方法一样。（关于Shi-Tomasi详细的内容，可以参考我的博客及我上传资源内的英文原文）

 （3）新的改进方法

Harris同KLT虽然说算法简单，理解不难，也具有一定程度的光强不变性，旋转不变性，及对噪声的一定鲁棒性，但计算量大，精确度不高，也不具有尺度及仿射不变性。

针对尺度不变性及仿射不变性，也有许多改进方法，主要是利用多尺度空间，在原来角响应度计算公式内引入了尺度参数，而仿射不变性的获得可以通过估计仿射矩阵，然后通过应用仿射矩阵将仿射区域变换成正圆区域，然后便应用尺度变换，如下图。（可以参考我的博客文章《尺度及仿射不变的Harris角特征点检测及匹配算法》及我上传资源内的英文原文。当然先前提到Shi-Tomasi方法也是应用仿射不变性角点检测方法的一种，不过其不是提取检测过程，而是在角点匹配过程中。

实时快速算法LOCOCO角点检测方法在2010年被提出，不过这种算法也没有从根本上改变Harris及KLT计算角响应的方法，而是在其基础上提高了运算速度，另外其2011年提出了子像素精度角点位置的改进S-LOCOCO方法，其针对KLT和Harris分别提出了SLC-KLT同SLC-Harris方法，这里的SLC的意思是子像素精度低复杂度。

其主要是针对于四个方面的改进：

A）在计算图像像素点梯度g时，需要通过高斯梯度模板，而这个模板可以通过盒函数来代替（SURF），而盒函数的卷积可以通过积分图像快速完成。

B）角响应其主要是通过每点的窗口内所有像素的梯度平方和乘积的带权值和，最后得到了二阶梯度矩阵。如果当窗口权值为1的话，那么窗口内的梯度平方和乘积和的计算肯定会出现重叠，而如果在积分图像的情况下，直接计算积分图像的各个梯度，将会让计算量大大减少。

C）NMS（非极大值抑制问题）：可以通过将图像分块（而不是一个个的像素点）来实施NMS，然后将每个块内的最大值找到，最后对于每个块内的最大值比较其邻域点，从而减少了我们需要排序的特征值数目。

D）子像素精度的角点位置确定：主要是通过角响应函数的二阶泰勒展开式，进行子像素精度插值。（关于LOCOCO算法的详细的内容，可以参考我的博客及我上传资源内的英文原文）

关于图像像素梯度的角点检测方法近年来，好的论文并不多，因为关于角点检测的方法越来越多，而新的优势却并不明显，不过若在计算速度和精度能大幅提高的话，也会大有可为的。

（4）改进后的精确度比较：

引入尺度不变性（多尺度空间）的结果：

引入仿射不变性后结果：

以上图表出自于Scale & Affine Invariant Interest PointDetectors,Krystianmikolajczyk and cordelia schmid (我上传的资源里面有原文)

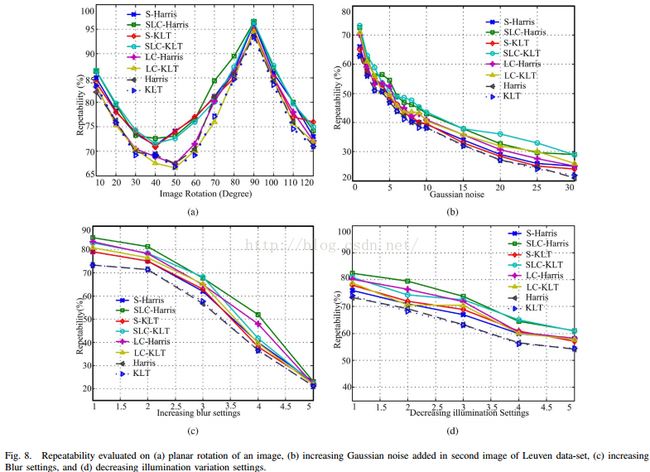
引入LOCOCO算法后的结果比较（如图中的SLC所示）

以上图表出自于Robust Low Complexity Corner Detector, Pradip Mainali (我上传的资源里面有原文)

三、基于拉布拉斯变换的检测子

拉布拉斯变换后的过零点可以用来检测角点，但也会引入噪声，所以一般我们采用平滑的拉布拉斯变换，也那是LOG方法，但拉布拉斯计算量较大，所以我们可以通过DOG方法来代替，而高斯卷积滤波也可以用迭代滤波器来近似，从而达到高速的效果。