RCNN学习笔记(3):From RCNN to SPP-net
CNN网络需要固定尺寸的图像输入,SPPNet将任意大小的图像池化生成固定长度的图像表示,提升R-CNN检测的速度24-102倍。
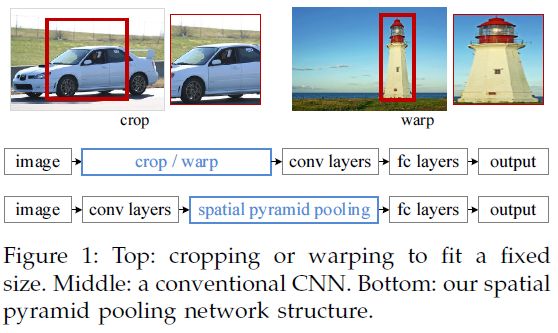
固定图像尺寸输入的问题,截取的区域未涵盖整个目标或者缩放带来图像的扭曲。事实上,CNN的卷积层不需要固定尺寸的图像,全连接层是需要固定大小输入的,因此提出了SPP层放到卷积层的后面,改进后的网络如下图所示:
SPP是BOW的扩展,将图像从精细空间划分到粗糙空间,之后将局部特征聚集。在CNN成为主流之前,SPP在检测和分类的应用比较广泛。SPP的优点:1)任意尺寸输入,固定大小输出,2)层多,3)可对任意尺度提取的特征进行池化。
说下池化,其实池化很容易理解,先看图:
R-CNN提取特征比较耗时,需要对每个warp的区域进行学习,而SPPNet只对图像进行一次卷积,之后使用SPPNet在特征图上提取特征。结合EdgeBoxes提取的proposal,系统处理一幅图像需要0.5s。
SPP层的结构如下,将紧跟最后一个卷积层的池化层使用SPP代替,输出向量大小为kM,k=#filters,M=#bins,作为全连接层的输入。至此,网络不仅可对任意长宽比的图像进行处理,而且可对任意尺度的图像进行处理。尺度在深层网络学习中也很重要。
网络训练:
multi-size训练,输入尺寸在[180,224]之间,假设最后一个卷积层的输出大小为 a×a ,若给定金字塔层有 n×n 个bins,进行滑动窗池化,窗口尺寸为 win=⌈a/n⌉ ,步长为 str=⌊a/n⌋ ,使用一个网络完成一个完整epoch的训练,之后切换到另外一个网络。只是在训练的时候用到多尺寸,测试时直接将SPPNet应用于任意尺寸的图像。
如果原图输入是224x224,对于conv5出来后的输出,是13x13x256的,可以理解成有256个这样的filter,每个filter对应一张13x13的reponse map。
如果像上图那样将reponse map分成4x4 2x2 1x1三张子图,做max pooling后,出来的特征就是固定长度的(16+4+1)x256那么多的维度了。
如果原图的输入不是224x224,出来的特征依然是(16+4+1)x256
直觉地说,可以理解成将原来固定大小为(3x3)窗口的pool5改成了自适应窗口大小,窗口的大小和reponse map成比例,保证了经过pooling后出来的feature的长度是一致的
Conclusion:
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
输入层:一张任意大小的图片,假设其大小为(w,h)。
输出层:21个神经元。
也就是我们输入一张任意大小的特征图的时候,我们希望提取出21个特征。空间金字塔特征提取的过程如下:
图片尺度划分
如上图所示,当我们输入一张图片的时候,我们利用不同大小的刻度,对一张图片进行了划分。上面示意图中,利用了三种不同大小的刻度,对一张输入的图片进行了划分,最后总共可以得到16+4+1=21个块,我们即将从这21个块中,每个块提取出一个特征,这样刚好就是我们要提取的21维特征向量。
第一张图片,我们把一张完整的图片,分成了16个块,也就是每个块的大小就是(w/4,h/4);
第二张图片,划分了4个块,每个块的大小就是(w/2,h/2);
第三张图片,把一整张图片作为了一个块,也就是块的大小为(w,h)
空间金字塔最大池化的过程,其实就是从这21个图片块中,分别计算每个块的最大值,从而得到一个输出神经元。最后把一张任意大小的图片转换成了一个固定大小的21维特征(当然你可以设计其它维数的输出,增加金字塔的层数,或者改变划分网格的大小)。上面的三种不同刻度的划分,每一种刻度我们称之为:金字塔的一层,每一个图片块大小我们称之为:windows size了。如果你希望,金字塔的某一层输出n*n个特征,那么你就要用windows size大小为:(w/n,h/n)进行池化了。
当我们有很多层网络的时候,当网络输入的是一张任意大小的图片,这个时候我们可以一直进行卷积、池化,直到网络的倒数几层的时候,也就是我们即将与全连接层连接的时候,就要使用金字塔池化,使得任意大小的特征图都能够转换成固定大小的特征向量,这就是空间金字塔池化的奥义(多尺度特征提取出固定大小的特征向量)
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Note :BoW -> SPM
(SPP的思想来源于SPM,然后SPM的思想来源自BoW。
关于BoW和SPM,找到了两篇相关的博文,就不在这里展开了。
第九章三续:SIFT算法的应用—目标识别之Bag-of-words模型
Spatial Pyramid 小结)
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
SPPNet对ImageNet2012分类结果
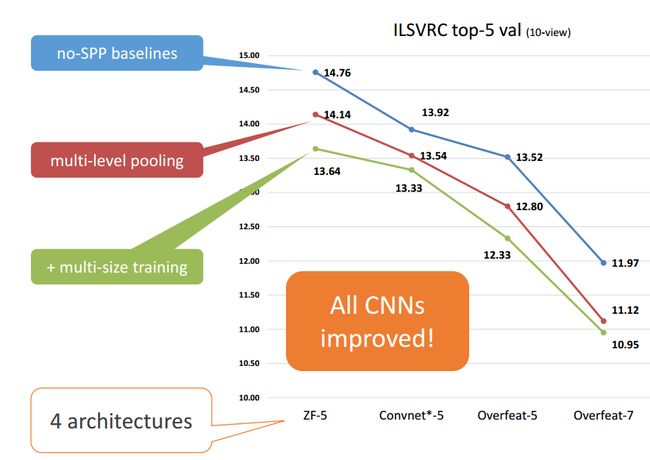
1).对已有网络增加SPP层提升系能,包括ZF-5,Convnet-5,Overfeat-5/7,单尺度和多尺度输入图像的实验结果top-1及top-5 error如下表所示,第一个提出多尺度输入图像训练网络
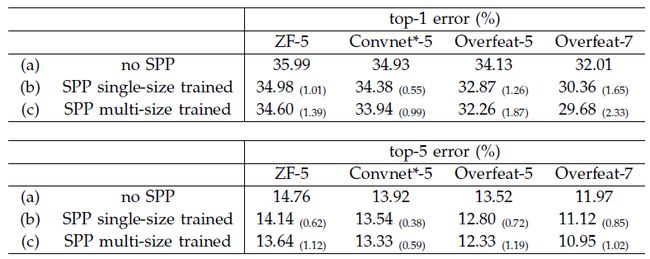
2).使用全图作为SPPNet的输入及224*224图像中心的crop对比,网络使用ZF-5,Overfeat-7,结果如下表

SPPNet for Object Detection
R-CNN重复使用深层卷积网络在~2k个窗口上提取特征,特征提取非常耗时。SPPNet比较耗时的卷积计算对整幅图像只进行一次,之后使用spp将窗口特征图池化为一个固定长度的特征表示。
检测算法:使用ss生成~2k个候选框,缩放图像min(w,h)=s之后提取特征,每个候选框使用一个4层的空间金字塔池化特征,网络使用的是ZF-5的SPPNet形式。之后将12800d的特征输入全连接层,SVM的输入为全连接层的输出。SVM如下使用,正样本为groundtruth,负样本与正样本的IoU<0.3,训练20类样本只需1h。使用ZF-5与R-CNN对比实验结果如下:
如何训练网络
理论上说,SPP-net支持直接以多尺度的原始图片作为输入后直接BP即可。实际上,caffe等实现中,为了计算的方便,输入是固定了尺度了的。
所以为了使得在固定输出尺度的情况下也能够做到SPP-net的效果,就需要定义一个新的SSP-layer
作者以输入224x224举例,这时候conv5出来的reponse map为13x13,计算出来的步长如下图所示。

具体的计算方法,看一眼2.3的Single-size training部分就明白了。
如果输入改成180x180,这时候conv5出来的reponse map为10x10,类似的方法,能够得到新的pooling参数。
两种尺度下,在SSP后,输出的特征维度都是(9+4+1)x256,之后接全连接层即可。
训练的时候,224x224的图片通过随机crop得到,180x180的图片通过缩放224x224的图片得到。之后,迭代训练,即用224的图片训练一个epoch,之后180的图片训练一个epoth,交替地进行。
如何测试网络
作者说了一句话:Note that the above single/multi-size solutions are for training only. At the testing stage, it is straightforward to apply SPP-net on images of any sizes.
笔者觉得没有那么简单吧,毕竟caffe对于test网络也是有固定尺度的要求的。
实验
之后是大量的实验。
分类实验
- 为了保证公平,test时候的做法是将图片缩放到短边为256,然后取10crop。这里的金字塔为{6x6 3x3 2x2 1x1}(笔者注意到,这里算是增加了特征,因为常规pool5后来说,只有6x6;这里另外多了9+4+1个特征)
- 作者将金字塔减少为{4x4 3x3 2x2 1x1},这样子,每个filter的feature从原来的36减少为30,但依然有提高。(笔者认为这个还是保留意见比较好)
- 其实这部分的实验比较多,详见论文,不在这里写了。
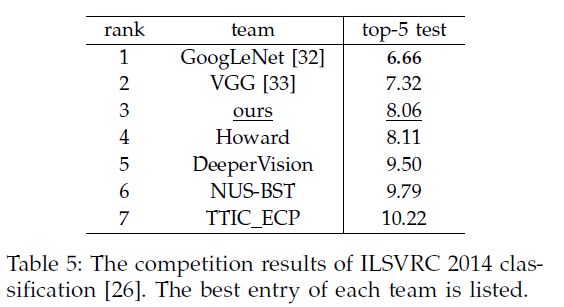
- 在ILSVRC14上的cls track,作者是第三名
定位实验
这里详细说说笔者较为关心的voc07上面的定位实验
用来对比的对象是RCNN。
方法简述:
- 提取region proposal部分依然用的是selective search
- CNN部分,结构用的是ZF-5(单尺度训练),金字塔用了{6x6 3x3 2x2 1x1},共50个bin
- 分类器也是用了SVM,后处理也是用了cls-specific regression
所以主要差别是在第二步,做出的主要改进在于SPP-net能够一次得到整个feature map,大大减少了计算proposal的特征时候的运算开销。
具体做法,将图片缩放到s∈{480,576,688,864,1200}的大小,于是得到了6个feature map。尽量让region在s集合中对应的尺度接近224x224,然后选择对应的feature map进行提取。(具体如何提取?后面的附录会说)
最后效果如图:

准确率从58.5提高到了59.2,而且速度快了24x
如果用两个模型综合,又提高了一点,到60.9
附录
如何将图像的ROI映射到feature map?
说实话,笔者还是没有完全弄懂这里的操作。先记录目前能够理解的部分。
总体的映射思路为:In our implementation, we project the corner point of a window onto a pixel in the feature maps, such that this corner point (in the image
domain) is closest to the center of the receptive field of that pixel.
略绕,我的理解是:
- 映射的是ROI的两个角点,左上角和右下角,这两个角点就可以唯一确定ROI的位置了。
- 将feature map的pixel映射回来图片空间
- 从映射回来的pixel中选择一个距离角点最近的pixel,作为映射。
这里有几个变量
- 139代表的是感受野的直径,计算这个也需要一点技巧了:如果一个filter的kernelsize=x,stride=y,而输出的reponse map的长度是n,那么其对应的感受野的长度为:n+(n-1)*(stride-1)+2*((kernelsize-1)/2)

- 16是effective stride,这里笔者理解为,将conv5的pixel映射到图片空间后,两个pixel之间的stride。(计算方法,所有stride连乘,对于ZF-5为2x2x2x2=16)
- 63和75怎么计算,还没有推出来
SPP详解
Reference Link:http://blog.csdn.net/xyy19920105/article/details/50817725
SPP网络,我不得不要先说,这个方法的思想在Fast RCNN, Faster RCNN上都起了举足轻重的作用。SPP网络主要是解决深度网络固定输入层尺寸的这个限制,也从各个方面说明了不限制输入尺寸带来的好处。文章在一开始的时候就说明了目前深度网络存在的弊端:如果固定网络输入的话,要么选择crop策略,要么选择warp策略,crop就是从一个大图扣出网络输入大小的patch(比如227×227),而warp则是把一个bounding box的内容resize成227×227 。无论是那种策略,都能很明显看出有影响网络训练的不利因素,比如crop就有可能crop出object的一个部分,而无法准确训练出类别,而warp则会改变object的正常宽高比,使得训练效果变差。接着,分析了出深度网络需要固定输入尺寸的原因是因为有全链接层,不过在那个时候,还没有FCN的思想,那如何去做才能使得网络不受输入尺寸的限制呢?Kaiming He 大神就想出,用不同尺度的pooling 来pooling出固定尺度大小的feature map,这样就可以不受全链接层约束任意更改输入尺度了。下图就是SPP网络的核心思想:
通过对feature map进行相应尺度的pooling,使得能pooling出4×4, 2×2, 1×1的feature map,再将这些feature map concat成列向量与下一层全链接层相连。这样就消除了输入尺度不一致的影响。训练的时候就用常规方法训练,不过由于不受尺度的影响,可以进行多尺度训练,即先resize成几个固定的尺度,然后用SPP网络进行训练,学习。这里讲了这么多,实际上我想讲的是下面的 东西, SPP如何用在检测上面。论文中实际上我觉得最关键的地方是提出了一个如何将原图的某个region映射到conv5的一种机制,虽然,我并不是太认可这种映射机制,等下我也会说出我认为合理的映射方法。论文中是如何映射的,实际上我也是花了好久才明白。
首先,我想先说明函数这个东东,当然我不是通过严谨的定义来说明。什么是y=f(x),我认为只要输入x,有一组固定的操作f,然后产生一个对应的y,这样子就算是函数。根据输入有一个一一对应的输出,这就是函数。这样理解的话,卷积也是函数,pooling也是函数。当然我并不想说明函数是什么,什么是函数,实际上我想强调的是一一对应这样的关系。大家都知道,现在默许的无论是卷积还是pooling(无stride),都会加相应的pad,来使得卷积后的尺寸与卷积前相同,当然这种做法还个好处就是使得边缘不会只被卷积一次就消失了~这样子的话,实际上原图与卷积后的图就是一一对应的关系。原图的每一个点(包括边缘)都可以卷积得到一个新的点,这就是一一对应了。如下图所示(自己画得太丑):

绿色部分是图片,紫色部分是卷积核。

如上图可以看出,蓝色的区域是原图区域,而红色的区域是padding区域,紫色的是卷积核。卷积后得到的区域与原区域是一一对应的。而卷积或pooling增加stride的话就相当与原图先进行卷积或池化,再进行sampling,这还是能一一对应的,就这样原图的某个区域就可以通过除以网络的所有stride来映射到conv5后去区域。终于把这里讲出来了,大家如果直接按照函数的一一对应关系去理解,很容易理解为什么原图的区域除以所有的stride就是映射到conv5的区域。这样子就可以在原图上的一些操作放在conv5上进行,这样可以减小任务复杂度。不过,我并不是太认可这种映射机制,这种映射只能是点到点的关系,不过我觉得从原图的某个区域R映射到conv5的区域r,应该r对R敏感,换句话说,应该r感受野应该与R有交集。这样子的话,示意图如下:
其中蓝色的为conv的神经元感受野,红色的是原图的某个感兴趣区域,而黑色框我才认为是要映射到conv5的区域。
使用SPP进行检测,先用提候选proposals方法(selective search)选出候选框,不过不像RCNN把每个候选区域给深度网络提特征,而是整张图提一次特征,再把候选框映射到conv5上,因为候选框的大小尺度不同,映射到conv5后仍不同,所以需要再通过SPP层提取到相同维度的特征,再进行分类和回归,后面的思路和方法与RCNN一致。实际上这样子做的话就比原先的快很多了,因为之前RCNN也提出了这个原因就是深度网络所需要的感受野是非常大的,这样子的话需要每次将感兴趣区域放大到网络的尺度才能卷积到conv5层。这样计算量就会很大,而SPP只需要计算一次特征,剩下的只需要在conv5层上操作就可以了。当然即使是这么完美的算法,也是有它的瑕疵的,可能Kaiming He大神太投入 SPP的功效了,使得整个流程框架并没有变得更加完美。首先在训练方面,SPP没有发挥出它的优势,依旧用了传统的训练方法,这使得计算量依旧很大,而且分类和bounding box的回归问题也可以联合学习,使得整体框架更加完美。这些Kaiming He都给忽略了,这样也就有了第二篇神作 Fast RCNN。
Reference Link http://zhangliliang.com/2014/09/13/paper-note-sppnet/