poj 1556 The Doors（线段交+最短路）

http://poj.org/problem?id=1556

The Doors

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7630		Accepted: 2981

Description

You are to find the length of the shortest path through a chamber containing obstructing walls. The chamber will always have sides at x = 0, x = 10, y = 0, and y = 10. The initial and final points of the path are always (0, 5) and (10, 5). There will also be from 0 to 18 vertical walls inside the chamber, each with two doorways. The figure below illustrates such a chamber and also shows the path of minimal length. 

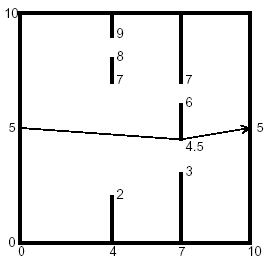
Input

The input data for the illustrated chamber would appear as follows. 

2 
4 2 7 8 9 
7 3 4.5 6 7 

The first line contains the number of interior walls. Then there is a line for each such wall, containing five real numbers. The first number is the x coordinate of the wall (0 < x < 10), and the remaining four are the y coordinates of the ends of the doorways in that wall. The x coordinates of the walls are in increasing order, and within each line the y coordinates are in increasing order. The input file will contain at least one such set of data. The end of the data comes when the number of walls is -1. 

Output

The output should contain one line of output for each chamber. The line should contain the minimal path length rounded to two decimal places past the decimal point, and always showing the two decimal places past the decimal point. The line should contain no blanks.

Sample Input

1
5 4 6 7 8
2
4 2 7 8 9
7 3 4.5 6 7
-1

Sample Output

10.00
10.06

题目大意：有一个房间（左上角（0，10），右下角（10,0）），然后房间里有N面墙，每面墙上都有两个门，求出来从初始点（0,5），到达终点（10，5）的最短距离。

根据线段交去判断会不会冲突，可以直接连的就建立一条路径。

昨天写的代码用G++交OLE了，冥思苦想不知道哪出错了，用G++交了一天，OLE了一天，我的小心脏，简直要崩溃，因为写的代码自我感觉真的是无懈可击，然后今天用C++交了一下就AC啦，脑残了，昨天怎么就没想到用C++交呢，不过为什么用C++交就对了呢

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<cmath>

using namespace std;

#define N 160
#define INF 0x3f3f3f3f
#define MOD
#define EPS 1e-8
#define met(a, b) memset(a, b, sizeof(a))

typedef long long LL;

using namespace std;

struct point
{
    double x, y;
} p[N];

int n, k, vis[N];
double g[N][N], dist[N];

double xmult (point p1, point p2, point p0)///叉积
{
    return (p1.x-p0.x) * (p2.y-p0.y) - (p2.x-p0.x) * (p1.y-p0.y);
}

double Dis (point a, point b)///两点间的距离
{
    return sqrt((a.x-b.x) * (a.x-b.x) + (a.y-b.y) * (a.y-b.y));
}

bool IsIntersected (point s1, point e1, point s2, point e2)///判断两线段相交
{
    return (max (s1.x, e1.x) >= min (s2.x, e2.x)) &&
           (max (s2.x, e2.x) >= min (s1.x, e1.x)) &&
           (max (s1.y, e1.y) >= min (s2.y, e2.y)) &&
           (max (s2.y, e2.y) >= min (s1.y, e1.y)) &&
           (xmult (s1, s2, e1) * xmult (s1, e1, e2) > 0) &&
           (xmult (s2, s1, e2) * xmult (s2, e2, e1) > 0);
}

bool Get_Dis (point Q1, point Q2, int l, int r)///判断两点之间能否之间到达
{
    for (int i=l+1; i<r; i++)
    {
        if (((i-1)/4 > (l-1)/4 && (i-1)/4 < (r-1)/4 && l) || (((i-1)/4 >= (l-1)/4 && (i-1)/4 < (r-1)/4 && !l)))
        {
            if ((i-1) % 4 == 0)
            {
                point Q;
                Q.x = p[i].x, Q.y = 0;
                if (IsIntersected (Q1, Q2, p[i], Q))
                    return false;
            }

            if ((i-1) % 4 == 1)
            {
                if (IsIntersected (Q1, Q2, p[i], p[i+1]))
                    return false;
            }

            if ((i-1) % 4 == 2)
            {
                if (IsIntersected (Q1, Q2, p[i], p[i-1]))
                    return false;
            }

            if ((i-1) % 4 == 3)
            {
                point Q;
                Q.x = p[i].x, Q.y = 10;
                if (IsIntersected (Q1, Q2, p[i], Q))
                    return false;
            }
        }
    }
    return true;
}

void Dij (int sa)///最短路
{
    met (vis, 0);
    dist[sa] = 0;
    for (int i=0; i<=k; i++)
        dist[i] = g[sa][i];

    for (int i=0; i<=k; i++)
    {
        int minx = INF, Index = 0;
        for (int j=0; j<=k; j++)
            if (!vis[j] && minx > dist[j])
                minx = dist[Index = j];

        vis[Index] = 1;

        for (int j=0; j<=k; j++)
            if (!vis[j] && dist[j] > g[Index][j] + dist[Index])
                dist[j] = g[Index][j] + dist[Index];
    }
}

void Solve ()
{
    for (int i=0; i<=k; i++)
    {
        for (int j=i+1; j<=k; j++)
        if (((j-1)/4 > (i-1)/4 && i) || ((j-1)/4 >= (i-1)/4 && !i))///判断j点是否和i点不在同一条线上
        if (Get_Dis (p[i], p[j], i, j))
            g[i][j] = Dis (p[i], p[j]);
    }

    Dij (0);
}

int main ()
{
    int n;
    while (scanf ("%d", &n), n!=-1)
    {
        met (p, 0);
        k = 0;
        p[k].x = 0, p[k++].y = 5;

        double x, y1, y2, y3, y4;

        for (int i=0; i<n; i++)
        {
            scanf ("%lf%lf%lf%lf%lf", &x, &y1, &y2, &y3, &y4);
            p[k].x = x, p[k++].y = y1;
            p[k].x = x, p[k++].y = y2;
            p[k].x = x, p[k++].y = y3;
            p[k].x = x, p[k++].y = y4;
        }

        p[k].x = 10, p[k].y = 5;

        for (int i=0; i<=k; i++)
        {
            dist[i] = INF;
            for (int j=0; j<=k; j++)
            {
                if (i == j) g[i][j] = 0;
                else g[i][j] = INF;
            }
        }

        Solve ();
        printf ("%.2f\n", dist[k]);
    }
    return 0;
}