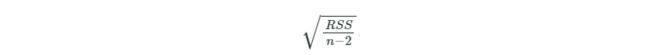Probability And Statistics In Python: Linear Regression

本文主要探索专业品酒师是怎么评估不同的白葡萄酒的强调内容下面是关于酒的一些特征以及样本：

density – shows the amount of material dissolved in the wine.（酒中材料的种类）
alcohol – the alcohol content of the wine.（酒精含量）
quality – the average quality rating (1-10) given to the wine.（平均质量等级(1 - 10）

“fixed acidity”,”volatile acidity”,”citric acid”,”residual sugar”,”chlorides”,”free sulfur dioxide”,”total sulfur dioxide”,”density”,”pH”,”sulphates”,”alcohol”,”quality”
7,0.27,0.36,20.7,0.045,45,170,1.001,3,0.45,8.8,6
6.3,0.3,0.34,1.6,0.049,14,132,0.994,3.3,0.49,9.5,6

• plot（）函数是用来画直线的

slope（斜率）

• 斜率可以通过cov(x,y)除以x的方差得到：

# The wine quality data is loaded into wine_quality
from numpy import cov
slope_density = cov(wine_quality["density"], wine_quality["quality"])[0, 1] / wine_quality["density"].var()

• 此处cov(wine_quality[“density”], wine_quality[“quality”])[0, 1]是因为cov这个函数是计算x和y的协方差矩阵，只有[0,1]表示的是x,y的协方差。

intercept（截距）

• 截距可以通过y的均值减去斜率倍的x的均值。

from numpy import cov

# This function will take in two columns of data, and return the slope of the linear regression line.
def calc_slope(x, y):
  return cov(x, y)[0, 1] / x.var()
intercept_density = wine_quality["quality"].mean() - (calc_slope(wine_quality["density"], wine_quality["quality"]) * wine_quality["density"].mean())

Making Predictions

from numpy import cov

def calc_slope(x, y):
  return cov(x, y)[0, 1] / x.var()

# Calculate the intercept given the x column, y column, and the slope
def calc_intercept(x, y, slope):
  return y.mean() - (slope * x.mean())
slope = calc_slope(wine_quality["density"], wine_quality["quality"])
intercept = calc_intercept(wine_quality["density"], wine_quality["quality"], slope)

def compute_predicted_y(x):
  return x * slope + intercept

predicted_quality = wine_quality["density"].apply(compute_predicted_y)
''' slope：-90.942399939553411 intercept：96.277144573482417 '''

Finding Error

from scipy.stats import linregress

# We've seen the r_value before -- we'll get to what p_value and stderr_slope are soon -- for now, don't worry about them.
slope, intercept, r_value, p_value, stderr_slope = linregress(wine_quality["density"], wine_quality["quality"])

# As you can see, these are the same values we calculated (except for slight rounding differences)
print(slope)
print(intercept)
import numpy
predicted_y = numpy.asarray([slope * x + intercept for x in wine_quality["density"]])
residuals = (wine_quality["quality"] - predicted_y) ** 2
rss = sum(residuals)
''' slope：-90.9423999421 intercept：96.2771445761 '''

Standard Error

• 前面求的误差是平方的形式，标准差就是平方误差的开方，有一点区别是此时还要除以n-2,n表示样本数：

  

• within_one ：计算在一个标准误差范围内的样本数

from scipy.stats import linregress
import numpy as np

# We can do our linear regression
# Sadly, the stderr_slope isn't the standard error, but it is the standard error of the slope fitting only
# We'll need to calculate the standard error of the equation ourselves
slope, intercept, r_value, p_value, stderr_slope = linregress(wine_quality["density"], wine_quality["quality"])

predicted_y = np.asarray([slope * x + intercept for x in wine_quality["density"]])
residuals = (wine_quality["quality"] - predicted_y) ** 2
rss = sum(residuals)
stderr = (rss / (len(wine_quality["quality"]) - 2)) ** .5

def within_percentage(y, predicted_y, stderr, error_count):
  within = stderr * error_count

  differences = abs(predicted_y - y)
  lower_differences = [d for d in differences if d <= within]

  within_count = len(lower_differences)
  return within_count / len(y)

within_one = within_percentage(wine_quality["quality"], predicted_y, stderr, 1)
within_two = within_percentage(wine_quality["quality"], predicted_y, stderr, 2)
within_three = within_percentage(wine_quality["quality"], predicted_y, stderr, 3)
'''