十大经典数据挖掘算法之K-Means算法
1、K-means算法简介
K-means是最简单的聚类算法之一,简单地说就是把相似的东西分到一组,同 Classification (分类)不同,对于一个 classifier ,通常需要你告诉它“这个东西被分为某某类”这样一些例子,理想情况下,一个 classifier 会从它得到的训练集中进行“学习”,从而具备对未知数据进行分类的能力,这种提供训练数据的过程通常叫做 supervised learning (监督学习),而在聚类的时候,我们并不关心某一类是什么,我们需要实现的目标只是把相似的东西聚到一起,因此,一个聚类算法通常只需要知道如何计算相似 度就可以开始工作了,K-means算法运用十分广泛,一般在数据分析前期使用,选取适当的k,将数据分类后,然后研究不同聚类下数据的特点。
2、K-Means聚类算法原理简介
K-means 算法接受参数k ;然后将事先输入的n个数据对象划分为 k个聚类以便使得所获得的聚类满足:同一聚类中的对象相似度较高;而不同聚类中的对象相似度较小。聚类相似度是利用各聚类中对象的均值所获得一个“中心对象”(引力中心)来进行计算的。
K-means算法是最为经典的基于划分的聚类方法,是十大经典数据挖掘算法之一。K-means算法的基本思想是:以空间中k个点为中心进行聚类,对最靠近他们的对象归类。通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。
假设要把样本集分为c个类别,算法描述如下:
(1)适当选择c个类的初始中心;
(2)在第k次迭代中,对任意一个样本,求其到c个中心的距离,将该样本归到距离最短的中心所在的类;
(3)利用均值等方法更新该类的中心值;
(4)对于所有的c个聚类中心,如果利用(2)(3)的迭代法更新后,值保持不变,则迭代结束,否则继续迭代。
该算法的最大优势在于简洁和快速。算法的关键在于初始中心的选择和距离公式。
3、算法原理详解
假设我们提取到原始数据的集合为(x1, x2, …, xn),并且每个xi为d维的向量,K-means聚类的目的就是,在给定分类组数k(k ≤ n)值的条件下,将原始数据分成k类
S = {S1, S2, …, Sk},在数值模型上,即对以下表达式求最小值:
这里μi 表示分类Si 的平均值。
那么在计算机编程中,其又是如何实现的呢?其算法步骤一般如下:
1、从D中随机取k个元素,作为k个簇的各自的中心。
2、分别计算剩下的元素到k个簇中心的相异度,将这些元素分别划归到相异度最低的簇。
3、根据聚类结果,重新计算k个簇各自的中心,计算方法是取簇中所有元素各自维度的算术平均数。
4、将D中全部元素按照新的中心重新聚类。
5、重复第4步,直到聚类结果不再变化。
6、将结果输出。
用数学表达式来说,
设我们一共有 N 个数据点需要分为 K 个 cluster ,k-means 要做的就是最小化
这个函数,其中 ![]() 在数据点 n 被归类到 cluster k 的时候为 1 ,否则为 0 。直接寻找
在数据点 n 被归类到 cluster k 的时候为 1 ,否则为 0 。直接寻找![]() 和
和![]() 来最小化
来最小化![]() 并不容易,不过我们可以采取迭代的办法:先固定
并不容易,不过我们可以采取迭代的办法:先固定![]() ,选择最优的
,选择最优的![]() ,很容易看出,只要将数据点归类到离他最近的那个中心就能保证
,很容易看出,只要将数据点归类到离他最近的那个中心就能保证![]() 最小。下一步则固定
最小。下一步则固定![]() ,再求最优的
,再求最优的![]() 。将
。将![]() 对
对![]() 求导并令导数等于零,很容易得到
求导并令导数等于零,很容易得到![]() 最小的时候
最小的时候![]() 应该满足:
应该满足:
亦即 ![]() 的值应当是所有 cluster k 中的数据点的平均值。由于每一次迭代都是取到
的值应当是所有 cluster k 中的数据点的平均值。由于每一次迭代都是取到![]() 的最小值,因此
的最小值,因此![]() 只会不断地减小(或者不变),而不会增加,这保证了 k-means 最终会到达一个极小值。虽然 k-means 并不能保证总是能得到全局最优解,但是对于这样的问题,像 k-means 这种复杂度的算法,这样的结果已经是很不错的了。
只会不断地减小(或者不变),而不会增加,这保证了 k-means 最终会到达一个极小值。虽然 k-means 并不能保证总是能得到全局最优解,但是对于这样的问题,像 k-means 这种复杂度的算法,这样的结果已经是很不错的了。
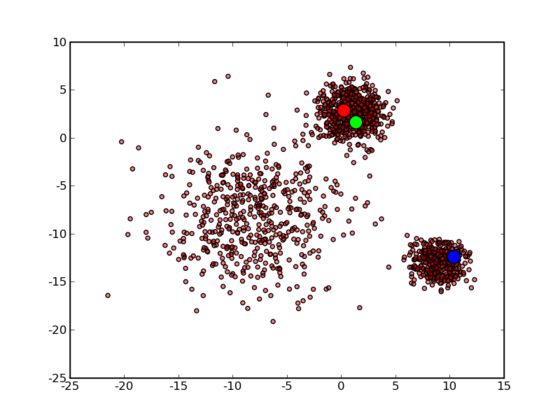
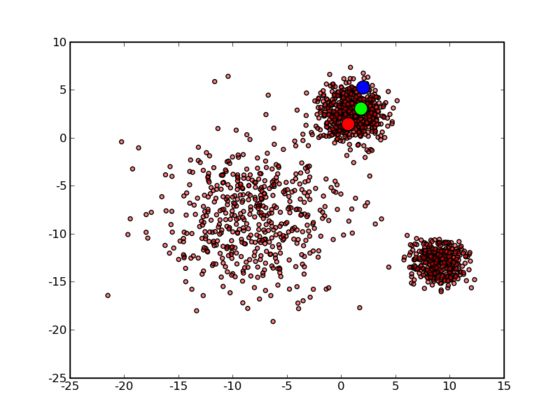
首先 3 个中心点被随机初始化,所有的数据点都还没有进行聚类,默认全部都标记为红色,如下图所示:
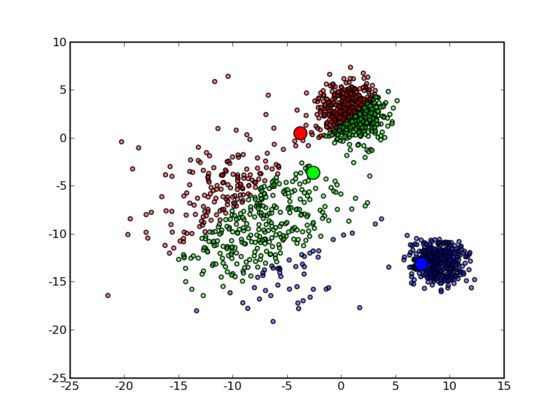
然后进入第一次迭代:按照初始的中心点位置为每个数据点着上颜色,重新计算 3 个中心点,结果如下图所示:
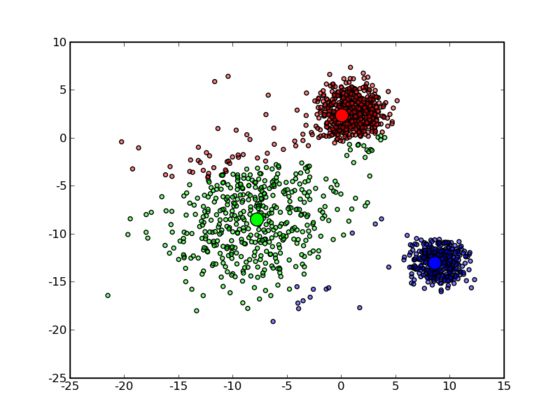
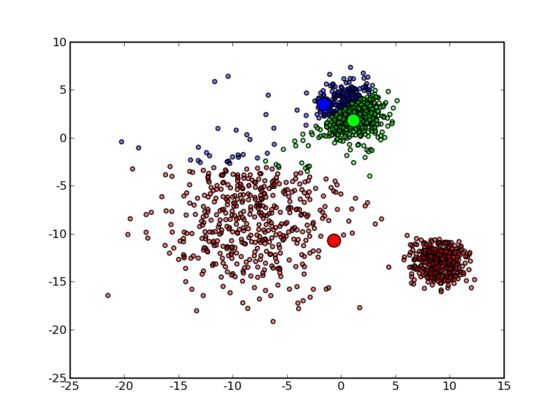
可以看到,由于初始的中心点是随机选的,这样得出来的结果并不是很好,接下来是下一次迭代的结果:
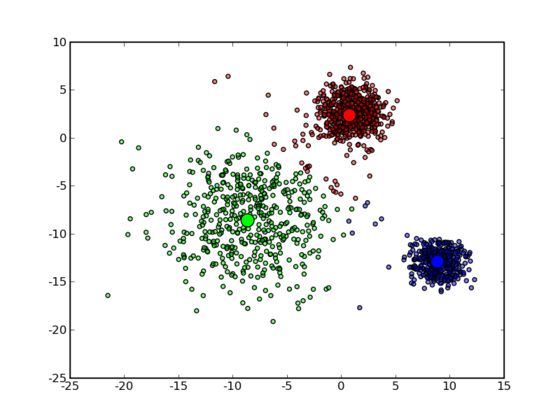
可以看到大致形状已经出来了。再经过两次迭代之后,基本上就收敛了,最终结果如下:
不过正如前面所说的那样 k-means 也并不是万能的,虽然许多时候都能收敛到一个比较好的结果,但是也有运气不好的时候会收敛到一个让人不满意的局部最优解,例如选用下面这几个初始中心点:
最终会收敛到这样的结果:
4、K-means算法的相似度度量
从算法原理可以看出,K-means算法最核心就是选取,相似度度量的计算公式,目前使用较多的有如下几种:
1)Minkowski Distance 公式 —— λ 可以随意取值,可以是负数,也可以是正数,或是无穷大。
2)Euclidean Distance 公式 —— 也就是第一个公式 λ=2 的情况
3)CityBlock Distance 公式 —— 也就是第一个公式 λ=1 的情况
这三个公式的求中心点有一些不一样的地方,我们看下图(对于第一个 λ 在 0-1之间)。
(1)Minkowski Distance (2)Euclidean Distance (3)CityBlock Distance
上面这几个图的大意是他们是怎么个逼近中心的,第一个图以星形的方式,第二个图以同心圆的方式,第三个图以菱形的方式。
5、K-means的问题及解决方案
K-means算法非常简单,然而却也有存在许多问题。
1)首先,算法只能找到局部最优的聚类,而不是全局最优的聚类。而且算法的结果非常依赖于初始随机选择的聚类中心的位置。我们通过多次运行算法,使用不同的随机生成的聚类中心点运行算法,然后对各自结果C通过evaluate(C)函数进行评估,选择多次结果中evaluate(C)值最小的那一个。
2)关于初始k值选择的问题。首先的想法是,从一个起始值开始,到一个最大值,每一个值运行k-means算法聚类,通过一个评价函数计算出最好的一次聚类结果,这个k就是最优的k。我们首先想到了上面用到的evaluate(C)。然而,k越大,聚类中心越多,显然每个观测点距离其中心的距离的平方和会越小,这在实践中也得到了验证。第四节中的实验结果分析中将详细讨论这个问题。
3)关于性能问题。原始的算法,每一次迭代都要计算每一个观测点与所有聚类中心的距离。有没有方法能够提高效率呢?是有的,可以使用k-d tree或者ball tree这种数据结构来提高算法的效率。特定条件下,对于一定区域内的观测点,无需遍历每一个观测点,就可以把这个区域内所有的点放到距离最近的一个聚类中去。这将在第三节中详细地介绍。