从Cheney算法->广度优先搜索->倒酒问题(JAVA实现)
转载请注明: http://blog.csdn.net/HEL_WOR/article/details/50446567
写JVM的垃圾回收的时候,提到了Minor GC时用到的Cheney算法。
在莫枢的回答里有一份他写的Chenny算法的实现,有兴趣的话可以直接进去看,不过他把算法放在了Gist上。Chenny算法和BFS很相似。如果先去读读《算法(第四版)》上BFS算法实现那节,就很容易看出Cheney在处理Survive From区对象Copy到Suevive To区和算法第4版上输出起始节点A到目标节点B的路径有多相似了。
不同之处:其一是Cheney算法中起始节点变成了多个(对应使用根遍历来搜索Active对象的多个根),其二是Chenny算法中对每一个遍历到的子节点的处理是将其复制到To区,并把父节点指向了复制到To区的对象。而在算法第四版上是对每一个遍历到的子节点记录其父节点地址或值以找到起始节点到目标节点的路径。
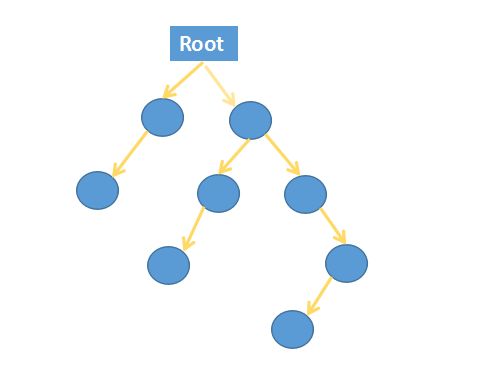
用图片来描述会好理解好多:
在画这张图的时候,我想起了消息队列,BFS算法使用到队列的作用就像是我们解决输入输出处理速度相差太大而引入的消息队列,在遍历到每一个根节点的子节点时都将这个子节点加入到队列,而每次从队列中取出的对象都做一次引用处理。队列的使用保证了先来先处理,但又不会导致先处理某个对象导致后来出现的对象丢失。
BFS算法的核心部分不是它的使用需要你提供什么条件,而是算法本身定义了一个遍历顺序,核心就是那段入队列和出队列的结构,队列的使用保证了你从顶向下的处理都是按照处理完第一层再处理下一层的顺序,不同的功能需求如处理引用关系(Cheney算法)和输出从A到B路径,都是在这个遍历顺序上实现的。
倒酒问题:
一个8L杯子装满了酒,有一个一个3L空杯子和一个5L空杯子,问怎样才能用最少的次数倒出4L的酒。(不能倒掉)
BFS算法本身就会保证第一次遇到目标节点就会结束搜索,这个功能是通过从上之下,从左至右依次遍历完成的。保证最少到达目标节点时从根节点到目标节点路径上的节点数是最少的;类似在地图上找从城市A到城市B的最少转乘路线。
倒酒问题就是三水杯问题的一个翻版。
可能对我来说最大的难度就是
- 如何把这3个杯子里的酒量所表示的状态和状态的改变抽象为一幅图。
- 状态的改变要满足那几个条件才算成功。
对第一个问题,现在3个水杯已有的状态是800,已经有一个点了,从这个点出发,每次状态的改变都会产生一个新的点xxx,那么这次状态的改变就可以作为连接800到xxx得边。现在就又回到了第二个问题:如何用函数定义一次状态的改变。
考虑两个数组,一个数组中保存的现有的状态avail[],另一个数组中保存的是每个杯子还剩余多少空间可以倒入酒need[]。
倒酒的几个限制条件:1,倒酒放的杯子里必须还有余量。
2,被倒入酒方的杯子不能是满的。
3,因为现在酒的总量是8,而3个杯子的最大容量分别是8,3,5;要构造出某个杯子中酒量为4的情况,因为8 = 3 + 5;如果每次杯子都被装满,我们是不能得到目的值4的,因此必须打破这种情况,也就是说倒酒方的avail不能和被倒酒方的need相等。
4,每次倒完酒只会有两种情况,倒酒方杯子空或者被倒酒方杯子满。所以当avail大于need时,该如何处理;当avail小于need时,又该如何处理。
5,状态不能回退,比如不能出现800->530->800的情况。
把这5个限制条件用代码描述出来,状态转移函数也就完成了。
package BFS;
import java.util.*;
public class StateTransfer {
/// <summary>
/// 每个杯子的现有酒量
/// </summary>
private static int[] avail;
/// <summary>
/// 每个杯子的现有酒量
/// </summary>
private static int[] availTemp;
/// <summary>
/// 每个杯子的还可装入的酒量
/// </summary>
private static int[] need;
/// <summary>
/// 每个杯子的还可装入的酒量
/// </summary>
private static int[] needTemp;
/// <summary>
/// 每个杯子的还可装入的酒量
/// </summary>
private static int[] capacityArr;
/// <summary>
/// 已存在的状态存记录
/// 用数组长度不好限定。。所有只能用链表了
/// </summary>
private static List<Integer> stateRecord = new ArrayList<Integer>();
/// <summary>
/// 扩展长度构造函数
/// </summary>
/// <param name="length">杯子个数</param>
public StateTransfer(int length)
{
avail = new int[length];
need = new int[length];
capacityArr = new int[length];
availTemp = new int[length];
needTemp = new int[length];
}
/// <summary>
/// 默认构造函数
/// </summary>
public StateTransfer()
{
avail = new int[3];
need = new int[3];
capacityArr = new int[3];
availTemp = new int[3];
needTemp = new int[3];
}
/// <summary>
/// 状态转移函数
/// </summary>
/// <param name="input">每个杯子的现有酒量</param>
/// <param name="capacity">每个杯子的最大容量</param>
/// <returns>所有子节点</returns>
public List<Integer> StateTransferMethod(int input, int capacity)
{
List<Integer> child = new ArrayList<Integer>();
//// 此次转移完成后的状态
int state = 0;
int inputLength = 0;
int calcLen = input;
while(calcLen != 0)
{
inputLength++;
calcLen /= 10;
}
//// 先填充数据
for (int i = 0; i < inputLength; i++)
{
// 以8561 千位/1000 个位%10 百位/100再%10 十位/10再%10
// 取最高位
if(i == 0)
{
avail[i] = (int)(input / Math.pow((double)10, (double)(inputLength - 1)));
capacityArr[i] = (int)(capacity / Math.pow((double)10, (double)(inputLength - 1)));
need[i] = capacityArr[i] - avail[i];
availTemp[i] = avail[i];
needTemp[i] = need[i];
}
// 取个位
if(i == inputLength - 1)
{
avail[i] = input % 10;
capacityArr[i] = capacity % 10;
need[i] = capacity % 10 - input % 10;
availTemp[i] = avail[i];
needTemp[i] = need[i];
}
// 0-inputLength之间
avail[i] = (int)(input / Math.pow((double)10, (double)(inputLength - 1 - i))) % 10;
capacityArr[i] = (int)(capacity / Math.pow((double)10, (double)(inputLength - 1 - i))) % 10;
need[i] = capacityArr[i] - avail[i];
availTemp[i] = avail[i];
needTemp[i] = need[i];
}
//// 再构造状态转移条件
for (int i = 0; i < inputLength; i++)
{
//// 如果杯子已满 已经不能再向其倒酒了 跳过
if (need[i] == 0)
{
continue;
}
//// 到达这一步表示杯子没满 其它可以向其倒酒以改变状态
for (int j = 0; j < inputLength; j++)
{
if (j == i)
{
continue;
}
//// 其他杯子里已经没酒了 不可能倒出酒来 跳过
if (avail[j] == 0)
{
continue;
}
//// 如果要倒出非杯子capacity的酒量 就必须打破达到容量值的倒法
if (need[i] == avail[j])
{
continue;
}
//// 走到这一步 则可以让其他杯子向其倒酒了
//// 不能让酒满出来
if (need[i] < avail[j])
{
//// 倒酒结束后要么倒酒方杯子空 要么被倒酒方杯子满
avail[i] = capacityArr[i];
//// 更新倒酒方余量
avail[j] = avail[j] - need[i];
//// 更新倒酒方所需
need[j] = need[j] + need[i];
}
else
{
avail[i] = avail[i] + avail[j];
need[i] = need[i] - avail[j];
avail[j] = 0;
need[j] = capacityArr[j];
}
state += avail[2] * 100 + avail[1] * 10 + avail[0] * 1;
//// 满足状态状态转移条件 但不能是已到达过的状态
//// 不能让状态回退 比如800-305-800
if (stateRecord.contains(new Integer(state)))
{
state = 0;
for (int k = 0; k < inputLength; k++)
{
avail[k] = availTemp[k];
need[k] = needTemp[k];
}
continue;
}
else
{
stateRecord.add(new Integer(state));
child.add(new Integer(state));
}
state = 0;
for (int k = 0; k < inputLength; k++)
{
avail[k] = availTemp[k];
need[k] = needTemp[k];
}
}
}
return child;
}
}
用Integer来描述状态有一个问题,就是你无法输入或者输出062,只能是62。可能需要用String来描述状态了,再用charAt(int index)来取出某个酒杯的当前酒量,改动太大,所以就这样吧。
现在状态转移函数写出来了,也就是说我们要构造出的图的顶点可以产生了,并且这些产生的顶点是有效并且不重复的,那么接下来就是
1.从根节点遍历出所有可达的有效顶点。
2.将遍历出的顶点指向其父节点以产生图的边。
到这一步我们就把倒酒问题抽象成一幅图了。产生这幅图的两个结构就是BFS和状态转移函数;我们需要重点内容实现的功能比如输出目标节点路径,对引用的处理(Cheney算法),根据要实现的功能的不同,在BFS算法出队列处实现不同的代码。
package BFS;
import java.util.*;
public class BreadthFirstSearch {
public static Queue<Integer> scaned = new LinkedList<Integer>();
public static Map<Integer, Integer> edgeToMap = new Hashtable<Integer, Integer>();
public static Map<Integer, Boolean> markedMap = new Hashtable<Integer, Boolean>();
private int oriState;
public void BFSMethod(int oriState, int capacity)
{
this.oriState = oriState;
scaned.offer(new Integer(oriState));
while (!scaned.isEmpty())
{
//// 对其每一个邻接点
int temp = scaned.poll();
List<Integer> child = new StateTransfer().StateTransferMethod(temp, capacity);
for (int item : child)
{
scaned.offer(new Integer(item));
//// 记录是否可达
markedMap.put(item, true);
//// 让子节点能找到其父节点
edgeToMap.put(item, temp);
}
}
}
public boolean IsPathExist(int targe)
{
if(markedMap.containsKey(targe))
{
return true;
}
return false;
}
public Stack<Integer> PathTo(int targe)
{
if(!this.IsPathExist(targe))
{
System.out.println(String.format("%d不可达", targe));
return null;
}
Stack<Integer> path = new Stack<Integer>();
for(int i = targe; i != this.oriState; i = edgeToMap.get(i))
{
path.push(new Integer(i));
}
path.push(new Integer(this.oriState));
return path;
}
}
使用Hashtable()来表示 子节点 ->父节点。思路类似于在子节点中保存父节点的地址,需要遍历路径时子节点就可能通过这个保存的地址找到父节点。不过这里面是直接保存父节点的值。
由于目标节点在未遍历到之前时不可见的,所以从根节点开始就记录路径时行不通的,这是一个树结构,所以不能用链表或者说线性的结构来记录路径,并且父子关系只会在相邻层产生,所以只能逆序的记录父节点的地址,找到目标节点后再迭代父节点直到找到根(类似不停跳转)。对于记录父节点,只要有键值对(或者说映射功能)的数据结构都能完成这个功能,数组也可以看做是隐含的键值对。
这个实现其实还有点问题,如果要显示出所有含4的状态还需要加点代码。
最后输出结果: