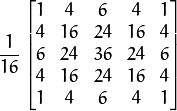图像金字塔
金字塔的底部是待处理的图像高分辨率表示,当向金字塔的上层移动时,尺寸和分辨率降低,伴随的细节就越少。金字塔的低分辨率级别用于分析大的结构或图像的整体内容;而高分辨率图像适合分析单个物体的特性。这种由粗到细的分析策略在模式识别中特别有用。
图像金字塔是多分辨率图像处理中的一项重要技术 。它实质上是根据原始图像构建出来的一个图像序列;序列中的每个图像称为一个层, 它们尺寸递减并均为原始图像的一个低分辨率表示 ;金字塔的相邻层之间, 分辨率一般相差两倍。最简单的一种是子抽样金字塔, 每一层图像由其前一层沿行、列两个方向等间隔抽样得到;其优点是构建速度快, 但生成的图像混淆显著, 像素对所在区域没有很好的代表性。均值金字塔则具有良好的视觉效果, 运算量也较小。高斯金字塔也具有良好的视觉效果, 但运算量略大。拉普拉斯金字塔由高斯金字塔派生而来,需要多读取部分数据才能够复原到高斯金字塔的效果。上述4种金字塔都比原始图像多出约1 /3的像素, 造成数据膨胀。Reduced-Sum金字塔则解决了数据膨胀问题, 它舍弃了部分像素, 从而使金字塔中的像素数等于原始图像。但Reduced-Sum金字塔存在精度截断的问题, 因为计算得到的低分辨率像素带有小数, 这些小数在舍入过程中被丢弃了, 使得原始图像无法精确恢复;否则, 每个像素需要多加两个比特来储存小数。实际上, 精度截断现象在现有各种金字塔普遍存在;只是像均值金字塔之类的冗余结构因为完整包含了原始图像, 所以允许小数被舍弃。------摘抄自《不产生精度截断及数据膨胀的图像金字塔》
金字塔表示中较高的层是下层平滑后的下采样形式, 原始图像层数等于零。当图像分解到一定的层后, 相邻帧间图像运动量将变得足够小, 满足光流计算的约束条件, 可以直接进行光流估计。在实际计算时, 由高层到低层进行, 当某一级的光流增量计算出来后, 将加到其初始值上, 再进行投影重建, 作为其下一层的光流计算初值。这一过程不断进行, 直至估计出原始图像的光流。 对原始图像I 中的特征点x(x , y ), 有L 层图像I L 中的x L (xL , y L )与之对应, 其中xL =x/
2L 。依据由粗至精的计算方式, 较高层上的误差将不断地向较低层传播和放大。因此, 在进行基于分层结构的光流计算时, 分解层数不能太多。------摘自《一种基于图像金字塔光流的特征跟踪方法》
图像金字塔
以多分辨率来解释图像的一种有效但概念简单的结构就是图像金字塔。图像金字塔最初用于机器视觉和图像压缩,一幅图像的金字塔是一系列以金字塔形状排列的分辨率逐步降低的图像集合。金字塔的底部是待处理图像的高分辨率表示,而顶部是低分辨率的近似。当向金字塔的上层移动时,尺寸和分辨率就降低。因为基础级J的尺寸是2^J*2^J或N*N(J=log2N),所以中间级j的尺寸是2^j*2^j,其中0<=j<=J。完整的金字塔由J+1个分辨率级组成,由2^J*2^J到2^0*2^0,但大部分金字塔只有P+1级,其中j=J-P,…,J-2,J-1,J,且1<=P<=J。也就是说通常限制它们只使用P级来减少原始图像近似值的尺寸。例如,一幅512*512图像的1*1或单像素近似值将非常小。右图显示了一个建立图像金字塔的简单系统。j-1级的近似输出用来建立近似值金字塔,包括原始图像的一个或多个近似值。作为金字塔的原始图像和它的P级减少的分辨率近似都能直接获取并调整。j级的预测残差输出用于建立预测残差金字塔。这些金字塔包括了原始图像的J-P级低分辨率的近似信息,以及建立P级较高分辨率的近似信息。j级的信息在相应近似金字塔的j级近似与基于j-1级预测残差得到的近似估计之间是不同的。对这些差异进行编码(用于存储或传输)将比对近似值进行编码有效得多。
图像金字塔建立和分类
近似值和预测残差金字塔都是以一种迭代的方式进行计算的。通过执行P次框图中的操作建立P+1级金字塔。第一次迭代和传递时,j=J,并且2^J*2^J的原始图像作为J级的输入图像,从而产生J-1级近似值和J级预测残差。对于j=J-1,J-2,…,J-P+1(按这一顺序)的传递,前面迭代的j-1级近似值输出将作为输入。每次传递由3个连续步骤组成:
高斯金字塔
-
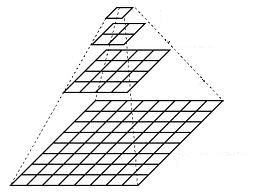
想想金字塔为一层一层的图像,层级越高,图像越小。
-
每一层都按从下到上的次序编号, 层级
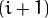 (表示为 尺寸小于层级
(表示为 尺寸小于层级  ())。
())。 -
为了获取层级为
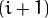 的金字塔图像,我们采用如下方法:
的金字塔图像,我们采用如下方法:-
将 与高斯内核卷积:
-
将所有偶数行和列去除。
-
-
显而易见,结果图像只有原图的四分之一。通过对输入图像
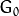 (原始图像) 不停迭代以上步骤就会得到整个金字塔。
(原始图像) 不停迭代以上步骤就会得到整个金字塔。 -
以上过程描述了对图像的向下采样,如果将图像变大呢?:
- 首先,将图像在每个方向扩大为原来的两倍,新增的行和列以0填充(
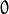 )
) - 使用先前同样的内核(乘以4)与放大后的图像卷积,获得 “新增像素” 的近似值。
- 首先,将图像在每个方向扩大为原来的两倍,新增的行和列以0填充(
-
这两个步骤(向下和向上采样) 分别通过OpenCV函数 pyrUp 和 pyrDown 实现, 我们将会在下面的示例中演示如何使用这两个函数。
本教程的源码如下,你也可以从 这里 下载
解释
-
让我们来回顾一下本程序的总体流程:
-
装载图像(此处路径由程序设定,用户无需将图像路径当作参数输入)
-
创建两个Mat实例, 一个用来储存操作结果(dst), 另一个用来存储零时结果(tmp)。
-
创建窗口显示结果
-
执行无限循环,等待用户输入。
如果用户按 ESC 键程序退出。 此外,它还提供两个选项:
-
向上采样 (按 ‘u’)
函数 pyrUp 接受了3个参数:
- tmp: 当前图像, 初始化为原图像 src 。
- dst: 目的图像( 显示图像,为输入图像的两倍)
- Size( tmp.cols*2, tmp.rows*2 ) : 目的图像大小, 既然我们是向上采样, pyrUp 期待一个两倍于输入图像( tmp )的大小。
-
向下采样(按 ‘d’)
类似于 pyrUp, 函数 pyrDown 也接受了3个参数:
- tmp: 当前图像, 初始化为原图像 src 。
- dst: 目的图像( 显示图像,为输入图像的一半)
- Size( tmp.cols/2, tmp.rows/2 ) :目的图像大小, 既然我们是向下采样, pyrDown 期待一个一半于输入图像( tmp)的大小。
-
注意输入图像的大小(在两个方向)必须是2的冥,否则,将会显示错误。
-
最后,将输入图像 tmp 更新为当前显示图像, 这样后续操作将作用于更新后的图像。
-
-