【STL源码剖析读书笔记】【第5章】关联式容器之RB-tree
1、 二叉树:任何节点最多只有两个子节点,这两个子节点分别称为左子节点和右子节点。
2、 二叉搜索树:任何节点的键值一定大于其左子树中的每一个节点的键值,小于其右子树中的每一个节点的键值。
3、 红黑树不仅是一个二叉搜索树,还必须满足以下条件:
1) 每个节点不是红色就是黑色。
2) 根节点为黑色。
3) 如果节点为红色,其子节点必须为黑色。
4) 任意一个节点到到NULL(树尾端)的任何路径,所含之黑色节点数必须相同。
根据规则4),新增节点必须为红色;根据规则3),新增节点之父节点必须为黑色。当新增节点根据二叉搜索树的规则到达其插入点时,却未能符合上述条件时,就必须调整颜色并旋转树形,如下图:
4、 红黑树插入节点
先为某些特殊节点定义一些代名:X代表新节点,P为其父节点,G为其祖父节点,S为其叔父节点,GG为其曾祖父节点。
插入操作分为以下几种情况:
一、P为黑
直接插入X,操作完成。
二、P为红
情况1:S为黑且X为外侧插入。
对P,G做一次右旋转操作并改变P,G的颜色,即可。
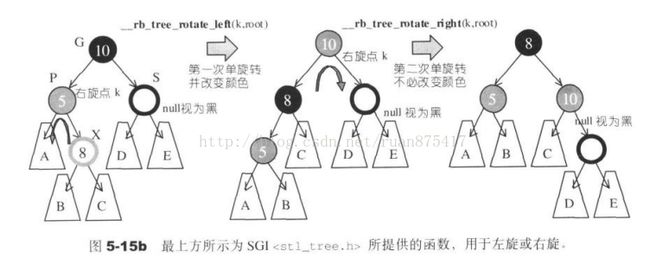
情况2:S为黑且X为内侧插入。
对P,X做一次左旋转操作并改变G,X的颜色,然后再对G做一次右旋转操作,即可。
情况3:S为红且X为外侧插入。
对P,G做一次右旋转操作改变X的颜色。此时如果GG为黑,操作完成。但如果GG为红,见情况4。
情况4:S为红且X为外侧插入,GG为红。
对P,G做一次右旋转操作改变X的颜色。GG为红,还得持续往上做,知道不再有父子连续为红的情况。
5、为避免插入节点的情况4,可以用自顶向下的方法:假设新增节点为A,就顺着A的路径,当遇到一个节点X的两个儿子都为红,就将X改为红,两个儿子改为黑。当X的父节点也为红使用情况1或情况2中的方法做调整。
6、红黑树节点结构
typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false; // 红色为0
const __rb_tree_color_type __rb_tree_black = true; // 黑色为1
struct __rb_tree_node_base
{
typedef __rb_tree_color_type color_type;
typedef __rb_tree_node_base* base_ptr;
color_type color; // 节点颜色,红色或黑色
base_ptr parent; // 该指针指向其父节点
base_ptr left; // 指向左节点
base_ptr right; // 指向右节点
static base_ptr minimum(base_ptr x)
{
while (x->left != 0) x = x->left; //一直向左走,找到最小值
return x;
}
static base_ptr maximum(base_ptr x)
{
while (x->right != 0) x = x->right; //一直向右走,找到最大值
return x;
}
};
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
typedef __rb_tree_node<Value>* link_type;
Value value_field; //节点值
};
7、
红黑树的迭代器
SGI将RB-tree迭代器实现分为两层。图5-16是两层节点结构和双层迭代器结构间的关系,其中主要意义是:__rb_tree_node继承自__rb_tree_node_base,__rb_tree_iterator继承自__rb_tree_base_iterator。
8、红黑树的元素操作
红黑树提供了两种插入操作:insert_unique()和insert_equal(),前者表示被插入节点的键值在树中插入独一无二,后者表示被插入节点的键值可以重复。
红黑树是一个二叉搜索树,元素的搜寻find()是其拿手项目。
9、红黑树源码
//stl_tree.h
#ifndef __SGI_STL_INTERNAL_TREE_H
#define __SGI_STL_INTERNAL_TREE_H
/*
Red-black tree(红黑树)class,用来当做SLT关联容器的底层机制(如set,multiset,map,
multimap)。里面所用的insertion和deletion方法以Cormen, Leiserson 和 Riveset所著的
《算法导论》一书为基础,但是有以下两点不同:
(1)header不仅指向root,也指向红黑树的最左节点,以便用常数时间实现begin(),并且也指向红黑树的最右边节点,以便
set相关泛型算法(如set_union等等)可以有线性时间实现。
(2)当一个即将被删除的节点有两个孩子节点时,它的successor(后继)node is relinked into its place, ranther than copied,
如此一来唯一失效的(invalidated)的迭代器就只是那些referring to the deleted node.
*/
#include <stl_algobase.h>
#include <stl_alloc.h>
#include <stl_construct.h>
#include <stl_function.h>
__STL_BEGIN_NAMESPACE
//定义红色黑色。红色为0,黑色为1
typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false;
const __rb_tree_color_type __rb_tree_black = true;
//红黑树节点双层结构的Base类
struct __rb_tree_node_base
{
typedef __rb_tree_color_type color_type;
typedef __rb_tree_node_base* base_ptr;
color_type color; // 节点颜色,非红即黑
base_ptr parent; // RB树的许多操作,必须知道其父结点
base_ptr left; // 指向左孩子节点。
base_ptr right; // 指向右孩子节点。
static base_ptr minimum(base_ptr x)
{
while (x->left != 0) x = x->left; // 一直向左走,就会找到最小值
return x; // 这是二叉查找树的性质。
}
static base_ptr maximum(base_ptr x)
{
while (x->right != 0) x = x->right;// 一直向右走,就会找到最大值
return x; // 这是二叉查找树的性质。
}
};
//红黑树节点双层结构的第二层,继承Base类
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
typedef __rb_tree_node<Value>* link_type;//指向节点的指针
Value value_field; // 节点的值
};
//迭代器基类,类型为bidirectional_iterator_tag,可以双向移动
struct __rb_tree_base_iterator
{
typedef __rb_tree_node_base::base_ptr base_ptr;//指向红黑树节点指针
typedef bidirectional_iterator_tag iterator_category;
typedef ptrdiff_t difference_type;
//指向红黑树节点的指针,用它来和容器产生关系
base_ptr node;
//下面只是为了实现oprerator++的,其他地方不会调用了。
//++是找到其后继节点
void increment()
{
//如果有右孩子,就是找右子树的最小值
if (node->right != 0) { // 如果有右孩子
node = node->right; // 就向右走
while (node->left != 0) // 然后向左走到底
node = node->left;
}
//如果无右子树。那么就找其最低祖先节点,且这个最低祖先节点的左孩子节点
//也是其祖先节点(每个节点就是自己的祖先节点)
else { // 没有右孩子
base_ptr y = node->parent; // 找出父节点
while (node == y->right) { // 如果现行节点本身是个右子节点
node = y; // 就一直上溯,直到“不为右子节点”止。
y = y->parent;
}
/*
若此时的右子节点不等于此时的父节点,此时的父节点即为解答,否则此时的node为解答.
这样做是为了应付一种特殊情况:我们欲寻找根节点的下一个节点。而恰巧根节点无右孩子。
当然,以上特殊做法必须配合RB-tree根节点与特殊header之间的特殊关系,在上面有图
*/
if (node->right != y) // 若此时的右子节点不等于此时的父节点
node = y; // 此时的父节点即为解答
// 否则此时的node为解答
}
}
//查找前驱结点。
void decrement()
{
if (node->color == __rb_tree_red && // 如果是红节点,且
node->parent->parent == node) // 父节点的父节点等于自己
node = node->right; // 状况(1) 右子节点即为解答。
/*
以上情况发生于node为header时(亦即node为end()时)。注意,header之右孩子即
mostright,指向整棵树的max节点。上面有图
*/
//左子树的最大值结点
else if (node->left != 0) {
base_ptr y = node->left;
while (y->right != 0)
y = y->right;
node = y;
}
/*
既非根节点,且无左子树。找其最低祖先节点y,且y的右孩子也是其祖先节点
*/
else {
base_ptr y = node->parent; //找出父节点
while (node == y->left) {
node = y;
y = y->parent;
}
node = y;
}
}
};
//RB-tree的正规迭代器
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator
{
typedef Value value_type;
typedef Ref reference;
typedef Ptr pointer;
typedef __rb_tree_iterator<Value, Value&, Value*> iterator;
typedef __rb_tree_iterator<Value, const Value&, const Value*> const_iterator;
typedef __rb_tree_iterator<Value, Ref, Ptr> self;
typedef __rb_tree_node<Value>* link_type;
//几个构造函数
__rb_tree_iterator() {}
__rb_tree_iterator(link_type x) { node = x; }
__rb_tree_iterator(const iterator& it) { node = it.node; }
//重载操作符
reference operator*() const { return link_type(node)->value_field; }
#ifndef __SGI_STL_NO_ARROW_OPERATOR
pointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */
//++做了封装,调用的是increment()
self& operator++() { increment(); return *this; }
self operator++(int) {
self tmp = *this;
increment();
return tmp;
}
//调用的是decrement
self& operator--() { decrement(); return *this; }
self operator--(int) {
self tmp = *this;
decrement();
return tmp;
}
};
//两个迭代器相等,意味着它们指向同一个红黑树节点
inline bool operator==(const __rb_tree_base_iterator& x,
const __rb_tree_base_iterator& y) {
return x.node == y.node;
}
inline bool operator!=(const __rb_tree_base_iterator& x,
const __rb_tree_base_iterator& y) {
return x.node != y.node;
}
#ifndef __STL_CLASS_PARTIAL_SPECIALIZATION
//返回迭代器类型
inline bidirectional_iterator_tag
iterator_category(const __rb_tree_base_iterator&) {
return bidirectional_iterator_tag();
}
inline __rb_tree_base_iterator::difference_type*
distance_type(const __rb_tree_base_iterator&) {
return (__rb_tree_base_iterator::difference_type*) 0;
}
template <class Value, class Ref, class Ptr>
inline Value* value_type(const __rb_tree_iterator<Value, Ref, Ptr>&) {
return (Value*)0;
}
#endif /* __STL_CLASS_PARTIAL_SPECIALIZATION */
// 以下都是全局函数:__rb_tree_rotate_left(), __rb_tree_rotate_right(),
// __rb_tree_rebalance(), __rb_tree_rebalance_for_erase()
/*
新节点必须为红色节点。如果安插处的父节点为红色,就违反了红黑色规则(3)。此时要旋转和改变颜色
*/
//左旋转
inline void
__rb_tree_rotate_left(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
// x 为旋转点
__rb_tree_node_base* y = x->right; // y为x的右孩子
x->right = y->left;
if (y->left != 0)
y->left->parent = x; // 别忘了回马枪设定父节点
y->parent = x->parent;
// 令 y 完全顶替 x 的地位(必须将x对其父节点的关系完全接收过来)
if (x == root) // x 为根节点
root = y;
else if (x == x->parent->left) // x 为父节点的左孩子
x->parent->left = y;
else // x 为父节点的右孩子
x->parent->right = y;
y->left = x;
x->parent = y;
}
//右旋转
inline void
__rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
// x 为旋转点
__rb_tree_node_base* y = x->left; // y为x的左孩子
x->left = y->right;
if (y->right != 0)
y->right->parent = x; // 別忘了回马枪设置父节点
y->parent = x->parent;
// 令 y 完全顶替 x 的地位(必须将x对其父节点的关系完全接收过来)
if (x == root) // x 为根节点
root = y;
else if (x == x->parent->right) // x 为父节点的右孩子
x->parent->right = y;
else // x 为父节点的左孩子
x->parent->left = y;
y->right = x;
x->parent = y;
}
//重新令RB-tree平衡(改变颜色和旋转)参数x为新增节点,参数二为root节点
inline void
__rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
x->color = __rb_tree_red; // 新节点比为红色
while (x != root && x->parent->color == __rb_tree_red) { // 父节点为红色
if (x->parent == x->parent->parent->left) { // 父节点为祖父节点的左孩子
__rb_tree_node_base* y = x->parent->parent->right; // 令y 为伯父节点
if (y && y->color == __rb_tree_red) { // 伯父节点存在,且为红色
x->parent->color = __rb_tree_black; // 更改父节点为黑色
y->color = __rb_tree_black; // 更改伯父节点为黑色
x->parent->parent->color = __rb_tree_red; // 更改祖父节点为红色
x = x->parent->parent;
}
else { // 无伯父节点或伯父节点为黑色(NULL就是黑色)
if (x == x->parent->right) { // 新增节点为父节点的右孩子
x = x->parent;
__rb_tree_rotate_left(x, root); // 第一个参数为左旋转点
}
x->parent->color = __rb_tree_black; // 改变颜色,父节点为黑色
x->parent->parent->color = __rb_tree_red;
__rb_tree_rotate_right(x->parent->parent, root); // 第一参数为右旋转点
}
}
else { // 父节点为祖父节点的右孩子
__rb_tree_node_base* y = x->parent->parent->left; // y为伯父节点
if (y && y->color == __rb_tree_red) { // 有伯父节点且为红色
x->parent->color = __rb_tree_black; // 更改父节点为黑色
y->color = __rb_tree_black; // 更改伯父节点为黑色
x->parent->parent->color = __rb_tree_red; // 更改祖父节点为红色
x = x->parent->parent; // 准备继续往上层检查……
}
else { // 无伯父节点或伯父节点为黑色(NULL就是黑色)
if (x == x->parent->left) { // 新节点为父节点的左孩子
x = x->parent;
__rb_tree_rotate_right(x, root); // 第一个参数右旋转
}
x->parent->color = __rb_tree_black; // 改变颜色,父节点为黑色
x->parent->parent->color = __rb_tree_red;
__rb_tree_rotate_left(x->parent->parent, root); // 第一个参数做旋转
}
}
} // while 結束
root->color = __rb_tree_black; // 根节点永远为黑色
}
//删除结点z
inline __rb_tree_node_base*
__rb_tree_rebalance_for_erase(__rb_tree_node_base* z,
__rb_tree_node_base*& root,
__rb_tree_node_base*& leftmost,
__rb_tree_node_base*& rightmost)
{
__rb_tree_node_base* y = z;
__rb_tree_node_base* x = 0;
__rb_tree_node_base* x_parent = 0;
if (y->left == 0) // z has at most one non-null child. y == z.
x = y->right; // x might be null.
else
if (y->right == 0) // z has exactly one non-null child. y == z.
x = y->left; // x is not null.
else { // z has two non-null children. Set y to
y = y->right; // z's successor. x might be null.
while (y->left != 0)
y = y->left;
x = y->right;
}
if (y != z) { // relink y in place of z. y is z's successor
z->left->parent = y;
y->left = z->left;
if (y != z->right) {
x_parent = y->parent;
if (x) x->parent = y->parent;
y->parent->left = x; // y must be a left child
y->right = z->right;
z->right->parent = y;
}
else
x_parent = y;
if (root == z)
root = y;
else if (z->parent->left == z)
z->parent->left = y;
else
z->parent->right = y;
y->parent = z->parent;
__STD::swap(y->color, z->color);
y = z;
// y now points to node to be actually deleted
}
else { // y == z
x_parent = y->parent;
if (x) x->parent = y->parent;
if (root == z)
root = x;
else
if (z->parent->left == z)
z->parent->left = x;
else
z->parent->right = x;
if (leftmost == z)
if (z->right == 0) // z->left must be null also
leftmost = z->parent;
// makes leftmost == header if z == root
else
leftmost = __rb_tree_node_base::minimum(x);
if (rightmost == z)
if (z->left == 0) // z->right must be null also
rightmost = z->parent;
// makes rightmost == header if z == root
else // x == z->left
rightmost = __rb_tree_node_base::maximum(x);
}
if (y->color != __rb_tree_red) {
while (x != root && (x == 0 || x->color == __rb_tree_black))
if (x == x_parent->left) {
__rb_tree_node_base* w = x_parent->right;
if (w->color == __rb_tree_red) {
w->color = __rb_tree_black;
x_parent->color = __rb_tree_red;
__rb_tree_rotate_left(x_parent, root);
w = x_parent->right;
}
if ((w->left == 0 || w->left->color == __rb_tree_black) &&
(w->right == 0 || w->right->color == __rb_tree_black)) {
w->color = __rb_tree_red;
x = x_parent;
x_parent = x_parent->parent;
}
else {
if (w->right == 0 || w->right->color == __rb_tree_black) {
if (w->left) w->left->color = __rb_tree_black;
w->color = __rb_tree_red;
__rb_tree_rotate_right(w, root);
w = x_parent->right;
}
w->color = x_parent->color;
x_parent->color = __rb_tree_black;
if (w->right) w->right->color = __rb_tree_black;
__rb_tree_rotate_left(x_parent, root);
break;
}
}
else { // same as above, with right <-> left.
__rb_tree_node_base* w = x_parent->left;
if (w->color == __rb_tree_red) {
w->color = __rb_tree_black;
x_parent->color = __rb_tree_red;
__rb_tree_rotate_right(x_parent, root);
w = x_parent->left;
}
if ((w->right == 0 || w->right->color == __rb_tree_black) &&
(w->left == 0 || w->left->color == __rb_tree_black)) {
w->color = __rb_tree_red;
x = x_parent;
x_parent = x_parent->parent;
}
else {
if (w->left == 0 || w->left->color == __rb_tree_black) {
if (w->right) w->right->color = __rb_tree_black;
w->color = __rb_tree_red;
__rb_tree_rotate_left(w, root);
w = x_parent->left;
}
w->color = x_parent->color;
x_parent->color = __rb_tree_black;
if (w->left) w->left->color = __rb_tree_black;
__rb_tree_rotate_right(x_parent, root);
break;
}
}
if (x) x->color = __rb_tree_black;
}
return y;
}
template <class Key, class Value, class KeyOfValue, class Compare,
class Alloc = alloc>
class rb_tree {
protected:
typedef void* void_pointer;
typedef __rb_tree_node_base* base_ptr;
typedef __rb_tree_node<Value> rb_tree_node;
typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;
typedef __rb_tree_color_type color_type;
public:
//这里没有定义iterator,在后面定义
typedef Key key_type;
typedef Value value_type;
typedef value_type* pointer;
typedef const value_type* const_pointer;
typedef value_type& reference;
typedef const value_type& const_reference;
typedef rb_tree_node* link_type;
typedef size_t size_type;
typedef ptrdiff_t difference_type;
protected:
link_type get_node() { return rb_tree_node_allocator::allocate(); }
void put_node(link_type p) { rb_tree_node_allocator::deallocate(p); }
link_type create_node(const value_type& x) {
link_type tmp = get_node(); // 配置空间
__STL_TRY{
construct(&tmp->value_field, x); // 构建内容
}
__STL_UNWIND(put_node(tmp));
return tmp;
}
link_type clone_node(link_type x) { // 复制一个节点(值和颜色)
link_type tmp = create_node(x->value_field);
tmp->color = x->color;
tmp->left = 0;
tmp->right = 0;
return tmp;
}
void destroy_node(link_type p) {
destroy(&p->value_field); // 析构内容
put_node(p); // 释放内存
}
protected:
// RB-tree 只以三个资料表现
size_type node_count; // 追踪记录树的大小(节点总数)
link_type header;
Compare key_compare; // 节点的键值比较判断准则。是个函数 function object。
//以下三个函数用来方便取得header的成员
link_type& root() const { return (link_type&)header->parent; }
link_type& leftmost() const { return (link_type&)header->left; }
link_type& rightmost() const { return (link_type&)header->right; }
//以下六个函数用来方便取得节点x的成员。x为函数参数
static link_type& left(link_type x) { return (link_type&)(x->left); }
static link_type& right(link_type x) { return (link_type&)(x->right); }
static link_type& parent(link_type x) { return (link_type&)(x->parent); }
static reference value(link_type x) { return x->value_field; }
static const Key& key(link_type x) { return KeyOfValue()(value(x)); }
static color_type& color(link_type x) { return (color_type&)(x->color); }
//和上面六个作用相同,注意x参数类型不同。一个是基类指针,一个是派生类指针
static link_type& left(base_ptr x) { return (link_type&)(x->left); }
static link_type& right(base_ptr x) { return (link_type&)(x->right); }
static link_type& parent(base_ptr x) { return (link_type&)(x->parent); }
static reference value(base_ptr x) { return ((link_type)x)->value_field; }
static const Key& key(base_ptr x) { return KeyOfValue()(value(link_type(x))); }
static color_type& color(base_ptr x) { return (color_type&)(link_type(x)->color); }
//找最大值和最小值。node class 有这个功能函数
static link_type minimum(link_type x) {
return (link_type)__rb_tree_node_base::minimum(x);
}
static link_type maximum(link_type x) {
return (link_type)__rb_tree_node_base::maximum(x);
}
public:
typedef __rb_tree_iterator<value_type, reference, pointer> iterator;
typedef __rb_tree_iterator<value_type, const_reference, const_pointer>
const_iterator;
#ifdef __STL_CLASS_PARTIAL_SPECIALIZATION
typedef reverse_iterator<const_iterator> const_reverse_iterator;
typedef reverse_iterator<iterator> reverse_iterator;
#else /* __STL_CLASS_PARTIAL_SPECIALIZATION */
typedef reverse_bidirectional_iterator<iterator, value_type, reference,
difference_type>
reverse_iterator;
typedef reverse_bidirectional_iterator<const_iterator, value_type,
const_reference, difference_type>
const_reverse_iterator;
#endif /* __STL_CLASS_PARTIAL_SPECIALIZATION */
private:
iterator __insert(base_ptr x, base_ptr y, const value_type& v);
link_type __copy(link_type x, link_type p);
void __erase(link_type x);
void init() {
header = get_node(); // 产生一个节点空间,令header指向它
color(header) = __rb_tree_red; // 令 header 尾红色,用來区 header
// 和 root(在 iterator.operator++ 中)
root() = 0;
leftmost() = header; // 令 header 的左孩子为自己。
rightmost() = header; // 令 header 的右孩子为自己。
}
public:
//默认构造函数 // allocation/deallocation
rb_tree(const Compare& comp = Compare())
: node_count(0), key_compare(comp) {
init();
}
// 以另一个 rb_tree x 初始化
rb_tree(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x)
: node_count(0), key_compare(x.key_compare)
{
header = get_node();
color(header) = __rb_tree_red;
if (x.root() == 0) { // 如果 x 空树
root() = 0;
leftmost() = header;
rightmost() = header;
}
else { // x 不是空树
__STL_TRY{
root() = __copy(x.root(), header); // 拷贝红黑树x
}
__STL_UNWIND(put_node(header));
leftmost() = minimum(root()); // 令 header 的左孩子为最小节点
rightmost() = maximum(root()); // 令 header 的右孩子为最大节点
}
node_count = x.node_count;
}
~rb_tree() {
clear();
put_node(header);
}
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>&
operator=(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x);
public:
// accessors:
Compare key_comp() const { return key_compare; }
iterator begin() { return leftmost(); } // RB 树的起始为最左(最小节点)
const_iterator begin() const { return leftmost(); }
iterator end() { return header; } // RB 树的终节点为header所指处
const_iterator end() const { return header; }
reverse_iterator rbegin() { return reverse_iterator(end()); }
const_reverse_iterator rbegin() const {
return const_reverse_iterator(end());
}
reverse_iterator rend() { return reverse_iterator(begin()); }
const_reverse_iterator rend() const {
return const_reverse_iterator(begin());
}
bool empty() const { return node_count == 0; }
size_type size() const { return node_count; }
size_type max_size() const { return size_type(-1); }
void swap(rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& t) {
//RB-tree只有三个资料表现成员,所以两颗RB-tree互换时,只需互换3个成员
__STD::swap(header, t.header);
__STD::swap(node_count, t.node_count);
__STD::swap(key_compare, t.key_compare);
}
public:
// insert/erase
// 将 x 安插到 RB-tree 中(保持节点值独一无二)。
pair<iterator, bool> insert_unique(const value_type& x);
// 将 x 安插到 RB-tree 中(允许重复节点)
iterator insert_equal(const value_type& x);
iterator insert_unique(iterator position, const value_type& x);
iterator insert_equal(iterator position, const value_type& x);
#ifdef __STL_MEMBER_TEMPLATES
template <class InputIterator>
void insert_unique(InputIterator first, InputIterator last);
template <class InputIterator>
void insert_equal(InputIterator first, InputIterator last);
#else /* __STL_MEMBER_TEMPLATES */
void insert_unique(const_iterator first, const_iterator last);
void insert_unique(const value_type* first, const value_type* last);
void insert_equal(const_iterator first, const_iterator last);
void insert_equal(const value_type* first, const value_type* last);
#endif /* __STL_MEMBER_TEMPLATES */
void erase(iterator position);
size_type erase(const key_type& x);
void erase(iterator first, iterator last);
void erase(const key_type* first, const key_type* last);
void clear() {
if (node_count != 0) {
__erase(root());
leftmost() = header;
root() = 0;
rightmost() = header;
node_count = 0;
}
}
public:
// 集合(set)的各种操作行为
iterator find(const key_type& x);
const_iterator find(const key_type& x) const;
size_type count(const key_type& x) const;
iterator lower_bound(const key_type& x);
const_iterator lower_bound(const key_type& x) const;
iterator upper_bound(const key_type& x);
const_iterator upper_bound(const key_type& x) const;
pair<iterator, iterator> equal_range(const key_type& x);
pair<const_iterator, const_iterator> equal_range(const key_type& x) const;
public:
// Debugging.
bool __rb_verify() const;
};
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
inline bool operator==(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x,
const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& y) {
return x.size() == y.size() && equal(x.begin(), x.end(), y.begin());
}
//重载<运算符,使用的是STL泛型算法<span style="font-family: Arial, Helvetica, sans-serif;">lexicographical_compare</span>
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
inline bool operator<(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x,
const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& y) {
return lexicographical_compare(x.begin(), x.end(), y.begin(), y.end());
}
#ifdef __STL_FUNCTION_TMPL_PARTIAL_ORDER
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
inline void swap(rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x,
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& y) {
x.swap(y);
}
#endif /* __STL_FUNCTION_TMPL_PARTIAL_ORDER */
//重载赋值运算符=
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>&
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::
operator=(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x) {
if (this != &x) {//防止自身赋值
// Note that Key may be a constant type.
clear();//先清除
node_count = 0;
key_compare = x.key_compare;
if (x.root() == 0) {
root() = 0;
leftmost() = header;
rightmost() = header;
}
else {
root() = __copy(x.root(), header);
leftmost() = minimum(root());
rightmost() = maximum(root());
node_count = x.node_count;
}
}
return *this;
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::
__insert(base_ptr x_, base_ptr y_, const Value& v) {
//参数x_为新值安插点,参数y_为安插点之父节点,参数v 为新值
link_type x = (link_type)x_;
link_type y = (link_type)y_;
link_type z;
//key_compare是键值得比较准则,是个函数或函数指针
if (y == header || x != 0 || key_compare(KeyOfValue()(v), key(y))) {
z = create_node(v); // 产生一个新节点
left(y) = z; // 这使得当y为header时,leftmost()=z
if (y == header) {
root() = z;
rightmost() = z;
}
else if (y == leftmost()) // 如果y为最左节点
leftmost() = z; // 维护leftmost(),使它永远指向最左节点
}
else {
z = create_node(v);
right(y) = z; // 令新节点成为安插点之父节点y的右孩子
if (y == rightmost())
rightmost() = z; // 维护rightmost(),使它永远指向最右节点
}
parent(z) = y; // 设定新节点的父节点
left(z) = 0; // 设定新孩子节点的左孩子
right(z) = 0; // 设定新孩子节点的右孩子
// 新节点的颜色将在 __rb_tree_rebalance() 设定并调整
__rb_tree_rebalance(z, header->parent); // 参数一为新增节点,参数二为root
++node_count; // 节点数增加
return iterator(z); // 返回迭代器,指向新增节点
}
// 安插新值;允许键值重复。返回新插入节点的迭代器
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_equal(const Value& v)
{
link_type y = header;
link_type x = root();
while (x != 0) { // 从根节点开始,向下寻找适当安插位置
y = x;
x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x);
}
return __insert(x, y, v);
}
/*
不允许键值重复,否则安插无效。
返回值是个pair,第一个元素是个RB-tree迭代器,指向新增节点。
第二个元素表示安插是否成功。
*/
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value& v)
{
link_type y = header;
link_type x = root(); //从根节点开始
bool comp = true;
while (x != 0) { // 从根节点开始向下寻找适当安插位置
y = x;
comp = key_compare(KeyOfValue()(v), key(x)); // v 键值小于目前节点的键值?
x = comp ? left(x) : right(x); // 遇「大」往左,遇「小于或等于」往右
}
//离开while循环之后,y所指即为安插点的父节点,x必为叶子节点
iterator j = iterator(y); // 令迭代器j指向安插点之父节点 y
if (comp) //如果离开while循环时comp为真,表示 父节点键值>v ,将安插在左孩子处
if (j == begin()) // 如果j是最左节点
return pair<iterator, bool>(__insert(x, y, v), true);
// 以上,x 为安插点,y 为安插点之父节点,v 为新值。
else // 否则(安插点之父节点不是最左节点)
--j; // 调整 j,回头准备测试...
if (key_compare(key(j.node), KeyOfValue()(v)))
// 小于新值(表示遇「小」,将安插于右侧)
return pair<iterator, bool>(__insert(x, y, v), true);
//若运行到这里,表示键值有重复,不应该插入
return pair<iterator, bool>(j, false);
}
template <class Key, class Val, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::insert_unique(iterator position,
const Val& v) {
if (position.node == header->left) // begin()
if (size() > 0 && key_compare(KeyOfValue()(v), key(position.node)))
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_unique(v).first;
else if (position.node == header) // end()
if (key_compare(key(rightmost()), KeyOfValue()(v)))
return __insert(0, rightmost(), v);
else
return insert_unique(v).first;
else {
iterator before = position;
--before;
if (key_compare(key(before.node), KeyOfValue()(v))
&& key_compare(KeyOfValue()(v), key(position.node)))
if (right(before.node) == 0)
return __insert(0, before.node, v);
else
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_unique(v).first;
}
}
template <class Key, class Val, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::insert_equal(iterator position,
const Val& v) {
if (position.node == header->left) // begin()
if (size() > 0 && key_compare(KeyOfValue()(v), key(position.node)))
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_equal(v);
else if (position.node == header) // end()
if (!key_compare(KeyOfValue()(v), key(rightmost())))
return __insert(0, rightmost(), v);
else
return insert_equal(v);
else {
iterator before = position;
--before;
if (!key_compare(KeyOfValue()(v), key(before.node))
&& !key_compare(key(position.node), KeyOfValue()(v)))
if (right(before.node) == 0)
return __insert(0, before.node, v);
else
return __insert(position.node, position.node, v);
// first argument just needs to be non-null
else
return insert_equal(v);
}
}
#ifdef __STL_MEMBER_TEMPLATES
template <class K, class V, class KoV, class Cmp, class Al> template<class II>
void rb_tree<K, V, KoV, Cmp, Al>::insert_equal(II first, II last) {
for (; first != last; ++first)
insert_equal(*first);
}
template <class K, class V, class KoV, class Cmp, class Al> template<class II>
void rb_tree<K, V, KoV, Cmp, Al>::insert_unique(II first, II last) {
for (; first != last; ++first)
insert_unique(*first);
}
#else /* __STL_MEMBER_TEMPLATES */
template <class K, class V, class KoV, class Cmp, class Al>
void
rb_tree<K, V, KoV, Cmp, Al>::insert_equal(const V* first, const V* last) {
for (; first != last; ++first)
insert_equal(*first);
}
template <class K, class V, class KoV, class Cmp, class Al>
void
rb_tree<K, V, KoV, Cmp, Al>::insert_equal(const_iterator first,
const_iterator last) {
for (; first != last; ++first)
insert_equal(*first);
}
template <class K, class V, class KoV, class Cmp, class A>
void
rb_tree<K, V, KoV, Cmp, A>::insert_unique(const V* first, const V* last) {
for (; first != last; ++first)
insert_unique(*first);
}
template <class K, class V, class KoV, class Cmp, class A>
void
rb_tree<K, V, KoV, Cmp, A>::insert_unique(const_iterator first,
const_iterator last) {
for (; first != last; ++first)
insert_unique(*first);
}
#endif /* __STL_MEMBER_TEMPLATES */
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
inline void
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::erase(iterator position) {
link_type y = (link_type)__rb_tree_rebalance_for_erase(position.node,
header->parent,
header->left,
header->right);
destroy_node(y);
--node_count;
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::size_type
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::erase(const Key& x) {
pair<iterator, iterator> p = equal_range(x);
size_type n = 0;
distance(p.first, p.second, n);
erase(p.first, p.second);
return n;
}
//复制x到p
template <class K, class V, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<K, V, KeyOfValue, Compare, Alloc>::link_type
rb_tree<K, V, KeyOfValue, Compare, Alloc>::__copy(link_type x, link_type p) {
// structural copy. x and p must be non-null.
link_type top = clone_node(x);
top->parent = p;
__STL_TRY{
if (x->right)
top->right = __copy(right(x), top);
p = top;
x = left(x);
while (x != 0) {
link_type y = clone_node(x);
p->left = y;
y->parent = p;
if (x->right)
y->right = __copy(right(x), y);
p = y;
x = left(x);
}
}
__STL_UNWIND(__erase(top));
return top;
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
void rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::__erase(link_type x) {
// erase without rebalancing
while (x != 0) {
__erase(right(x));
link_type y = left(x);
destroy_node(x);
x = y;
}
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
void rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::erase(iterator first,
iterator last) {
if (first == begin() && last == end())
clear();
else
while (first != last) erase(first++);
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
void rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::erase(const Key* first,
const Key* last) {
while (first != last) erase(*first++);
}
//查找RB树中是否有键值为k的节点
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::find(const Key& k) {
link_type y = header; // Last node which is not less than k.
link_type x = root(); // Current node.
while (x != 0)
// key_compare 是 function object。
if (!key_compare(key(x), k))
// 运行到这里,表示x键值大于k。遇到大值就向左走。
y = x, x = left(x); // 注意语法!逗号表达式
else
// 运行到这里,表示x键值小于k。遇到小值就向右走。
x = right(x);
iterator j = iterator(y);
return (j == end() || key_compare(k, key(j.node))) ? end() : j;
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::const_iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::find(const Key& k) const {
link_type y = header; /* Last node which is not less than k. */
link_type x = root(); /* Current node. */
while (x != 0) {
if (!key_compare(key(x), k))
y = x, x = left(x);
else
x = right(x);
}
const_iterator j = const_iterator(y);
return (j == end() || key_compare(k, key(j.node))) ? end() : j;
}
//计算RB树中键值为k的节点的个数
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::size_type
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::count(const Key& k) const {
pair<const_iterator, const_iterator> p = equal_range(k);
size_type n = 0;
distance(p.first, p.second, n);
return n;
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::lower_bound(const Key& k) {
link_type y = header; /* Last node which is not less than k. */
link_type x = root(); /* Current node. */
while (x != 0)
if (!key_compare(key(x), k))
y = x, x = left(x);
else
x = right(x);
return iterator(y);
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::const_iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::lower_bound(const Key& k) const {
link_type y = header; /* Last node which is not less than k. */
link_type x = root(); /* Current node. */
while (x != 0)
if (!key_compare(key(x), k))
y = x, x = left(x);
else
x = right(x);
return const_iterator(y);
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::upper_bound(const Key& k) {
link_type y = header; /* Last node which is greater than k. */
link_type x = root(); /* Current node. */
while (x != 0)
if (key_compare(k, key(x)))
y = x, x = left(x);
else
x = right(x);
return iterator(y);
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::const_iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::upper_bound(const Key& k) const {
link_type y = header; /* Last node which is greater than k. */
link_type x = root(); /* Current node. */
while (x != 0)
if (key_compare(k, key(x)))
y = x, x = left(x);
else
x = right(x);
return const_iterator(y);
}
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
inline pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator,
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::equal_range(const Key& k) {
return pair<iterator, iterator>(lower_bound(k), upper_bound(k));
}
template <class Key, class Value, class KoV, class Compare, class Alloc>
inline pair<typename rb_tree<Key, Value, KoV, Compare, Alloc>::const_iterator,
typename rb_tree<Key, Value, KoV, Compare, Alloc>::const_iterator>
rb_tree<Key, Value, KoV, Compare, Alloc>::equal_range(const Key& k) const {
return pair<const_iterator, const_iterator>(lower_bound(k), upper_bound(k));
}
//计算从 node 至 root路径中的黑节点数量
inline int __black_count(__rb_tree_node_base* node, __rb_tree_node_base* root)
{
if (node == 0)
return 0;
else {
int bc = node->color == __rb_tree_black ? 1 : 0;
if (node == root)
return bc;
else
return bc + __black_count(node->parent, root); // 累加
}
}
//验证己身这棵树是否符合RB树条件
template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
bool
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::__rb_verify() const
{
// 空树,符合RB树标准
if (node_count == 0 || begin() == end())
return node_count == 0 && begin() == end() &&
header->left == header && header->right == header;
//最左(叶)节点至 root 路径的黑节点个数
int len = __black_count(leftmost(), root());
//一下走访整个RB树,针对每个节点(从最小奥最大)……
for (const_iterator it = begin(); it != end(); ++it) {
link_type x = (link_type)it.node; // __rb_tree_base_iterator::node
link_type L = left(x); // 这是左子节点
link_type R = right(x); // 这是右子节点
if (x->color == __rb_tree_red)
if ((L && L->color == __rb_tree_red) ||
(R && R->color == __rb_tree_red))
return false; // 父子节点同为红色,不合符RB树要求
if (L && key_compare(key(x), key(L))) // 当前节点的键值小于左孩子节点的键值
return false; // 不符合二叉查找树的要求
if (R && key_compare(key(R), key(x))) // 当前节点的键值大于右孩子节点的键值
return false; // 不符合二叉查找树的要求
//[叶子结点到root]路径内的黑色节点数,与[最左节点至root]路径内的黑色节点不同。不符合RB树要求
if (!L && !R && __black_count(x, root()) != len)
return false;
}
if (leftmost() != __rb_tree_node_base::minimum(root()))
return false; // 最左节点不为最小节点,不符合二叉查找树的要求。
if (rightmost() != __rb_tree_node_base::maximum(root()))
return false; // 最右节点不为最大节点,不符不符合二叉查找树的要求。
return true;
}
__STL_END_NAMESPACE
#endif /* __SGI_STL_INTERNAL_TREE_H */
// Local Variables:
// mode:C++
// End: