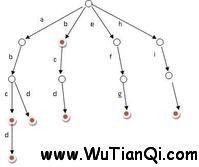
trie树——字典树
Trie树,又称单词查找树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来节约存储空间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
字典树与字典很相似,当你要查一个单词是不是在字典树中,首先看单词的第一个字母是不是在字典的第一层,如果不在,说明字典树里没有该单词,如果在就在该字母的孩子节点里找是不是有单词的第二个字母,没有说明没有该单词,有的话用同样的方法继续查找.字典树不仅可以用来储存字母,也可以储存数字等其它数据。
Trie的数据结构定义:
struct node//初始tire树
{
int num;//标记是否为相同前缀最后字符
node *next[max];//后继结点
};
next是表示每层有多少种类的数,如果只是小写字母,则26即可,若改为大小写字母,则是52,若再加上数字,则是62了,这里根据题意来确定。
sum可以表示一个字典树到此有多少相同前缀的数目,这里根据需要应当学会自由变化。
Trie的查找(最主要的操作):
(1) 每次从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索; (3) 在相应的子树上,取得要查找关键词的第二个字母,并进一步选择对应的子树进行检索。
(4) 迭代过程……
(5) 在某个结点处,关键词的所有字母已被取出,则读取附在该结点上的信息,即完成查找。
这里给出生成字典树和查找的模版:
生成字典树:
void insert(char ss[])//插入操作
{
node *p=root,*t;//p指向当前节点,t用来开辟内存
for(int i=0;ss[i];i++)//将每个字符存起来的过程
{
if(p->next[ss[i]-'a']==NULL)//当p指向为空的时候,需要开辟新的节点
{
t=new node;
t->num=0;
for(int i=0;i<max;i++)
t->next[i]=NULL;
p->next[ss[i]-'a']=t;//接上新的节点
}
p=p->next[ss[i]-'a'];//p指向下一个节点
p->num++;//
}
}
接下来是查找的过程了:
void search(char ss[])//查找
{
node *p=root;//p指向根节点
int t=0;
for(int i=0;ss[i];i++)
{
p=p->next[ss[i]-'a'];//p指向下一结点
if(p->num>1)
{
tt[t]=ss[i];
t++;
}
if(p->num==1)
{
tt[t]=ss[i];
tt[t+1]='\0';
return;
}
}
tt[t]='\0';//这个是防止上面的p->num都是大于1的
return ;
}
tt[]数组是输出将所有字符串可以区别的前缀
一些总结!!!!!!
动态指针版!!! 优点代码简短,缺点容易超内存,费时间
struct node//初始tire树
{
int num;//标记是否为相同前缀最后字符
node *next[max];//后继结点
};
node *root; //建立根节点的引用
void trie()//初始tire 树
{
int i,j;
root=new node;//为根节点开辟内存
root->num=0;
for(int i=0;i<max;i++)
root->next[i]=NULL;
}
void insert(char ss[])//插入操作
{
node *p=root,*t;//p指向当前节点,t用来开辟内存
for(int i=0;ss[i];i++)//将每个字符存起来的过程
{
if(p->next[ss[i]-'a']==NULL)//当p指向为空的时候,需要开辟新的节点
{
t=new node;
t->num=0;
for(int i=0;i<max;i++)
t->next[i]=NULL;
p->next[ss[i]-'a']=t;//接上新的节点
}
p=p->next[ss[i]-'a'];//p指向下一个节点
p->num++;//
}
}
void search(char ss[])//查找
{
node *p=root;//p指向根节点
int t=0;
for(int i=0;ss[i];i++)
{
p=p->next[ss[i]-'a'];//p指向下一结点
if(p->num>1)
{
tt[t]=ss[i];
t++;
}
if(p->num==1)
{
tt[t]=ss[i];
tt[t+1]='\0';
return;
}
}
tt[t]='\0';//这个是防止上面的p->num都是大于1的
return ;
}
tt[]数组是输出将所有字符串可以区别的前缀
静态数组版!!!!优点速度较快
struct node
{
bool isword;
int next[max];
void init()
{
memset(next,0,sizeof(next));
isword=false;
}
}tree[100010];
void insert(char a[])
{
int cou=0;
int index=0;
int len=strlen(a);
for(int i=0;i<len;i++)
{
if(tree[index].next[a[i]-'0']==0)
{
tree[++num].init();//建立新节点
tree[index].next[a[i]-'0']=num;//连接
index=num;
}
else
{
Cou++;
index=tree[index].next[a[i]-'0'];
if(tree[index].isword)
{
ok=false;
return;
}
}
}
tree[index].isword=true;
If(cou==len)
Ok=false;
}
Ok将返回所有字符串是否有一个为其他前缀