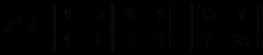[图像] 奇异值分解与隐性语义分析

     对于一个mxn大小的矩阵，可以分解为以下三个矩阵的乘积。

 

    其中，U和V都是正交矩阵（矩阵与其倒置矩阵的乘积为单位矩阵），是对角矩阵（对角线外的值都是0）。

    进行SVD分解的方法：
    首先要知道矩阵的秩，也就是最大线性不相关的行（列）向量的个数，比如对于以下两个矩阵

     

    矩阵1           矩阵2

     第一个矩阵两行（列）是线性相关的，所以秩为1，第二个矩阵两行（列）不是线性相关的，所以秩为2。

    由特征向量可求得矩阵U，由的特征向量可求得矩阵V，两者特征根是一样的，为，它们的开方是对角线上的值（注意对角矩阵值为正，并且从左上到右下呈递减趋势）。对于秩为r的矩阵，其特征根有r个，也就是对角线上非0的值有r个。

    以V为例：

 

    求特征根：

    则特征向量为和，平方和归一化，并把两个列向量拼接成矩阵，得到:   

    同理可以求得U=

    则A的SVD分解为

    特别地，如果矩阵A是一个对称正定矩阵，那么它得到的U，V是一样的。

    对于大小为mxn的矩阵来说，如果矩阵的秩为r，那么我们对于得到的结果，取mxk，kxk,，kxn大小部分进行重建。如果k等于r，那么我们可以重建得到和原矩阵完全一样的矩阵，如果k小于r，那么我们会得到和原矩阵相近的矩阵。后者过滤掉了一些不那么重要的噪声信息。

    根据最小二乘法，重建的矩阵与原矩阵差的平方和是最小的，所以是最终和最好的分解。

    SVD分解相当于把一个存在着信息冗余的矩阵投影到特征空间中，在这个空间中，蕴含着相似信息之间的关联关系。所以利用SVD分解，我们可以进行隐性语义分析。

    如果每个列向量代表一个文档，每个行向量代表某个单词在不同文档中出现的次数，那么我们就得到了原始的单词-文档矩阵，对单词-文档矩阵进行奇异值分解。选取k个特征根进行矩阵重建，k就是单词-文档空间的隐性因子。

    U的每一列向量是一个单词向量，前k列向量组成主题空间。V’ 的每一行向量是一个文档（单词词袋）。重建的过程就像借助于特征根将单词收纳入文档中。它可以将没有出现在同一篇文章中但具有相近含义的单词的关联性体现出来。

    重建的结果会出现正负，就可以很好地将单词与不同文档的关联区分开来，也就是可以通过重建的结果来分析。也可以将用户请求矩阵和单词-文档矩阵同时映射到k-维空间，进行相似度运算，然后反馈最相近的前几个文档。