机器学习之神经网络bp算法推导
这是一篇学习UFLDL反向传导算法的笔记,按自己的思路捋了一遍,有不对的地方请大家指点。
首先说明一下神经网络的符号:
1. nl 表示神经网络的层数。
2. sl 表示第 l 层神经元个数,不包含偏置单元。
3. z(l)i 表示第 l 层第 i 个神经元的输入; a(l)i 表示第 l 层第 i 个神经元的输出。
4. W(l)ij 表示第 l 层第 j 个神经元连接到第 l+1 层第 i 个神经元的权重,因此权值矩阵 W 的维数为 sl+1 x sl

第二层各神经元的计算方法如下:
我们可以将其向量化表示:
这里的矩阵 W 的具体形式为:
第 2 层的神经元个数为 4 ,第 1 层神经元的个数为 3 ,因此为 4×3 维的矩阵。
代价函数
对于单个样本我们将神经网络的代价函数定义为:
对所有 K 个样本,神经网络的总的代价函数(这也是批量的由来)为:
使用批量梯度下降算法寻求神经网络的最优参数
我们使用批量梯度下降算法寻求神经网络的最优参数 W(l),bl 。
我们先来看对于 第 l+1 层第 i 个神经元来说,第 l 层第 j 个神经元的权值可按如下方式迭代更新:
类似的,对于 第 l+1 层第 i 个神经元来说,第 l 层的偏置单元的权值可按如下方式迭代更新:
我们现在的目的是求出以下两个式子就可以对参数进行迭代了:
又我们知道第 l+1 层第 i 个神经元的输入 z(l+1)i 可以由以下式子计算:
再进一步的对上面的式子进行变形:
同样的,对于 b(l)i 的偏导数:
残差的定义
接下来我们定义:
为第 k 个样本在第 l 层第 i 个神经元上产生的残差。再次回顾我们的参数更新公式:
对于 W(l)ij 我们有:
类似的,对于 b(l)i 我们有:
现在的核心问题只剩下一个了,这个残差该如何求?
我们先计算最后一层第 i 个神经元上的残差,这里为了简单起见,不再指定为第 k 个样本。
然后计算倒数第二层即第 nl−1 层第 i 个神经元的残差:
下面是残差传播的示意图:
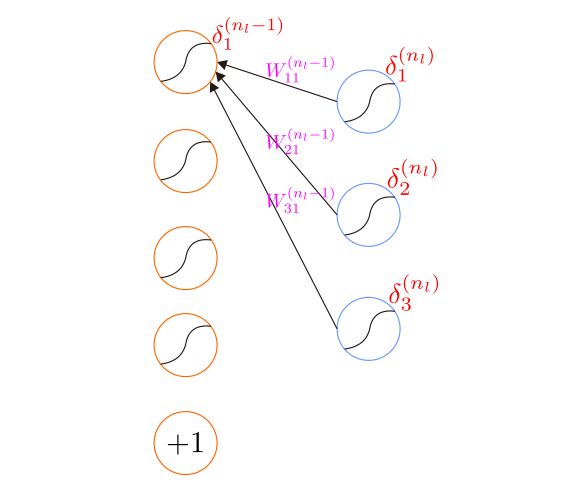
从这里可以看出紧挨着的两层神经元之间的残差是有关系的,这也是反向传播的由来。更一般的,可以将上述关系表述为:
再再次回顾我们的参数更新公式:
我们需要先计算输出层神经元的残差,然后一级一级的计算前一层的神经元的残差,利用这些残差就可以更新神经网络参数了。
向量化表示
这里我们尝试将上述结果表示成向量或矩阵的形式,比如我们希望能一次性更新某一层神经元的权值和偏置,而不是一个一个的更新。
δ(l+1)i 表示的是第 l+1 层第 i 个神经元的残差,那么整个第 l+1 层神经元的偏差是多少呢?
从而得到:
注:这里的 ∙ 是指点乘,即对应元素相乘, δ(l+1) 是一个 sl+1×1 维的列向量。
a(l)j 表示第 l 层第 j 个神经元的输出,因此整个第 l 层的神经元的输出可用 a(l) 表示,是一个 sl×1 维的列向量。
因此对于矩阵 W(l) 来说,我们记:
我们将 ΔW(l) 初始化为 0 ,然后对所有 K 个样本将它们的 ∇W(l)J(W,b;x,y) 累加到 ΔW(l) 中去:
然后更新一次 W(l) :
这里再强调一下:上式中的 ΔW(l) 是所有 K 个样本的 δ(l+1)(a(l))T 累加和,如果希望做随机梯度下降了或者是mini-batch,这里就不用把所有样本的残差加起来了。
类似的,令:
我们将 Δb(l) 初始化为 0 , 然后对所有 K 个样本将它们的 ∇b(l)J(W,b;x,y) 累加到 Δb(l) 中去
于是有:
同样的,上式中的 Δb(l) 是所有 K 个样本的 δ(l+1) 累加和。
小结
上面的推导过程尝试把所有的步骤都写出来了,个人感觉比UFLDL上的教程更为详尽,只要你耐心看总能看得懂的。当然这篇文章有些细节并未作说明,比如惩罚因子的作用,为什么没有对偏置进行规则化,激活函数的选择等,这些都可以在UFLDL中找到答案,对应的链接在下面的参考中给出。
参考
[1] 神经网络
[2] 反向传导算法