基于三叉链表存储结构的二叉树的不用栈的非递归遍历
三叉链表和二叉链表的不同在于,三叉链表多了一个parent指针域,指向双亲节点。便于访问双亲节点。
有了这个parent指针域,我们就能实现不用栈的非递归遍历二叉树。
现在,让我们来看看基于三叉链表存储结构的二叉树定义:
/***************************************************************************
* This is TriTree headfile
* **************************************************************************/
#ifndef TEST1_TRITREE_H_
#define TEST1_TRITREE_H_
class TriTNode;
typedef TriTNode *TriTree;
typedef int TElemType;
class TriTNode { // The node complemented by triadius link list
public :
TriTNode() {
}
TriTNode(TElemType data, TriTree parent);
~TriTNode();
public :
void Insert(TElemType data);
void Unite(TriTree L, TriTree R);
public :
TElemType data;
TriTree lchild, rchild, parent;
};
#endif//TEST1_TRITREE_H_
因为这片博文只要讲遍历,因此,不在这里对二叉树的构造做解释,只是给出代码,不想看的可以直接跳过,看遍历代码。只需要知道,最后得出的二叉树是具有二叉排序树特征的就行了(如果左子树不为空,则左子树上的所有结点的值均小于根结点;如果它的右子树不为空,那么右子树所有的结点的值均大于根结点,它的左右子树也是二叉排序树)。
/*****************************************************************
* This is TriTree complemention file
* ****************************************************************/
#include "TriTree.h"
#include <iostream>
TriTNode::TriTNode(TElemType data, TriTree parent) {
this->data = data;
lchild = NULL;
rchild = NULL;
this->parent = parent;
}
void TriTNode::Insert(TElemType data) {
if (data > this->data) {
if (rchild != NULL) {
rchild->Insert(data);
}
else {
TriTree node_ptr = new TriTNode(data, this);
rchild = node_ptr;
}
}
else if (data < this->data) {
if (lchild != NULL) {
lchild->Insert(data);
}
else {
TriTree node_ptr = new TriTNode(data, this);
lchild = node_ptr;
}
}
}
void TriTNode::Unite(TriTree L, TriTree R) {
if(lchild != NULL || rchild != NULL)
{
return ;
}
lchild = L;
rchild = R;
if (L != NULL) {
L->parent = this;
}
if (R != NULL) {
R->parent = this;
}
}
好了,现在就到了,main函数了(注:CreateTriTree函数是构造整个二叉树的,可以不看,不会影响到遍历算法的理解。):
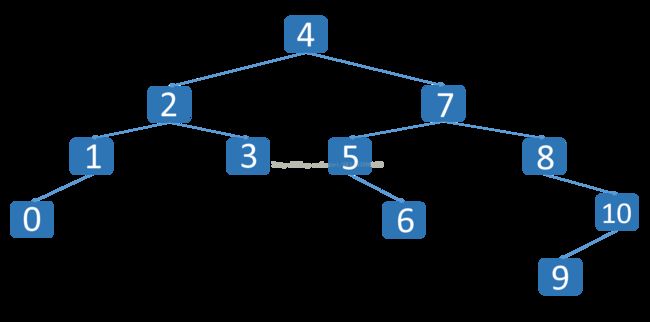
在这里先给出初始化的二叉树:
/************************************************************************
* main.cpp
* ***********************************************************************/
#include "TriTree.h"
#include <iostream>
TriTree CreateTriTree(TElemType data[], const int n) {
if(n <= 0) {
return NULL;
}
TriTree T = new TriTNode(data[0], NULL);
for (int i = 1; i < n; ++i) {
T->Insert(data[i]);
}
return T;
}
void PreOrderTraverse_Recursion(TriTree T) {
if (NULL == T) {
return ;
}
std::cout << T->data << " ";
PreOrderTraverse_Recursion(T->lchild);
PreOrderTraverse_Recursion(T->rchild);
}
void InOrderTraverse_Recursion(TriTree T) {
if (NULL == T) {
return ;
}
InOrderTraverse_Recursion(T->lchild);
std::cout << T->data << " ";
InOrderTraverse_Recursion(T->rchild);
}
void PostOrderTraverse_Recursion(TriTree T) {
if (NULL == T) {
return ;
}
PostOrderTraverse_Recursion(T->lchild);
PostOrderTraverse_Recursion(T->rchild);
std::cout << T->data << " ";
}
void PreOrderTraverse_NoRecursion(TriTree T) {
if (NULL == T) {
return ;
}
TriTree p, pr;
p = T;
while (p != NULL) {
std::cout << p->data << " ";
if (p->lchild != NULL) {
//循环实现的左子树的递归
p = p->lchild;
}
else if (p->rchild != NULL){
//如果左子树递归到底了,就递归右子树
p = p->rchild;
}
else {
//关键在于怎么回溯到双亲结点
//这个循环是往回查找第一个有右子树的结点
//当p == NULL的时候意味着,是从整棵树根结点往回查找。
//当p->lchild != p时,表明,这是从右子树往回查找,继续往回查找
//当p->lchild == p && p->rchild != NULL的时候,就找到了第一个没有被访问的右子树
do {
pr = p;
p = p->parent;
} while (p != NULL && (p->lchild != pr || NULL == p->rchild));
if (p != NULL) {
p = p->rchild;
}
}
}
}
void InOrderTraverse_NoRecursion(TriTree T) {
if (NULL == T) {
return ;
}
TriTree p, pr;
p = T;
while(NULL != p)
{
if (p->lchild != NULL) {
//和先序遍历不同,中序遍历是先递归左子树再输出结点。
p = p->lchild;
}
else {
//左子树递归结束,输出当前结点,并判断是否有右子树
//如果有右子树,则递归右子树
std::cout << p->data << " ";
if (p->rchild != NULL) {
p =p->rchild;
}
else {
//回溯双亲结点,同样是找到第一个没有被访问的右子树
//细微的差距就是,因为在递归左子树的过程中,并没有输出双亲结点。
//因此,在回溯的过程中,如果是从左回溯双亲结点的话,要输出双亲结点
//这个和递归的思想是一样的。
pr = p;
p = p->parent;
while (p != NULL && (p->lchild != pr || NULL == p->rchild)) {
if (p->lchild == pr) {
std::cout << p->data << " ";
}
pr = p;
p = p->parent;
}
if (NULL != p) {
std::cout << p->data << " ";
p = p->rchild;
}
}
}
}
}
void PostOrderTraverse_NoRecursion(TriTree T) {
if (NULL == T) {
return ;
}
TriTree p, pr;
p = T;
while (p != NULL) {
if (p->lchild != NULL){
p = p->lchild;
}
else {
//在左子树递归结束的时候,判断当前结点是否有右子树
//按照后序遍历的顺序,如果有右子树的话,是先输出右子树,再到根结点
if (p->rchild != NULL) {
p =p->rchild;
}
else {
//在左子树递归结束的条件下,
//如果没有右子树的话,就输出当前结点并回溯双亲结点。
std::cout << p->data << " ";
pr = p;
p = p->parent;
while(p != NULL && (p->lchild != pr || NULL == p->rchild)) {
//如果是从右回溯的话,就说明,这时候的左子树和右子树都被输出了,
//这时候双亲结点就应该被输出。
if(p->rchild == pr || p->rchild == NULL) {
std::cout << p->data << " ";
}
pr = p;
p = p->parent;
}
if(NULL != p) {
p = p->rchild;
}
}
}
}
}
int main(void) {
TElemType data[] = {4, 2, 1, 7, 5, 6, 3, 0, 8, 10, 9};
TriTree T;
T = CreateTriTree(data, sizeof(data) / sizeof(data[0]));
std::cout << "PreOrderTraverse : " << std::endl;
PreOrderTraverse_NoRecursion(T);
std::cout << std::endl;
PreOrderTraverse_Recursion(T);
std::cout << std::endl;
std::cout << "InOrderTraverse : " << std::endl;
InOrderTraverse_NoRecursion(T);
std::cout << std::endl;
InOrderTraverse_Recursion(T);
std::cout << std::endl;
std::cout << "PostOrderTraverse : " << std::endl;
PostOrderTraverse_NoRecursion(T);
std::cout << std::endl;
PostOrderTraverse_Recursion(T);
std::cout << std::endl;
system("PAUSE");
return 0;
}
其实这种遍历方法并不难,关键是首先要理解递归是怎么做的。
以先序遍历为例:
递归的做法就是先访问头结点,然后递归左子树,然后递归右子树。
非递归的做法其实也是基于递归的思想的实现。通过循环实现递归深入。然后通过parent不断的回溯双亲结点,并在回溯的过程,找到没有被访问的右子树。