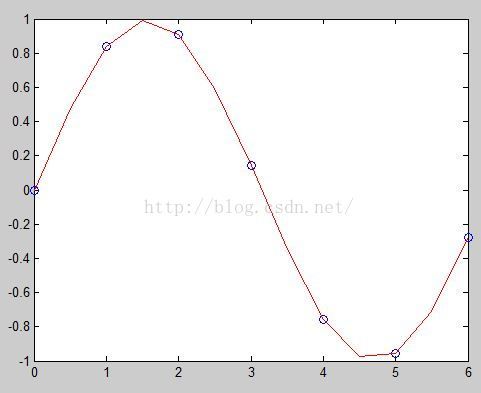
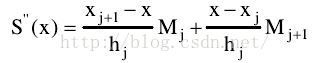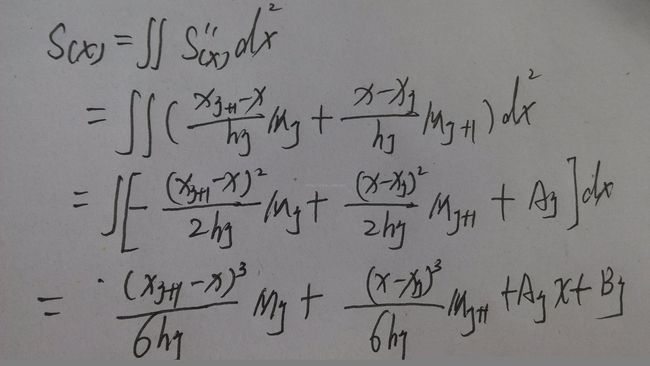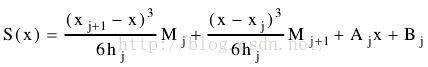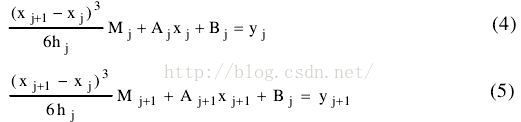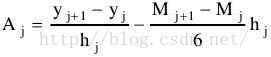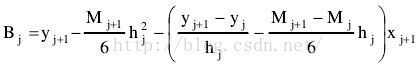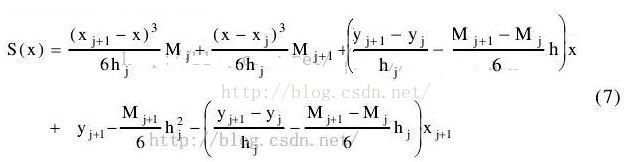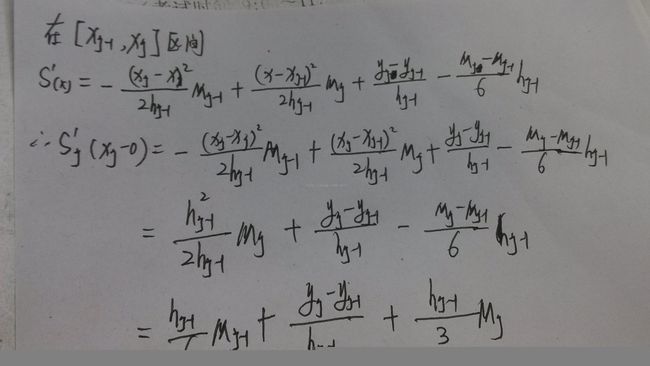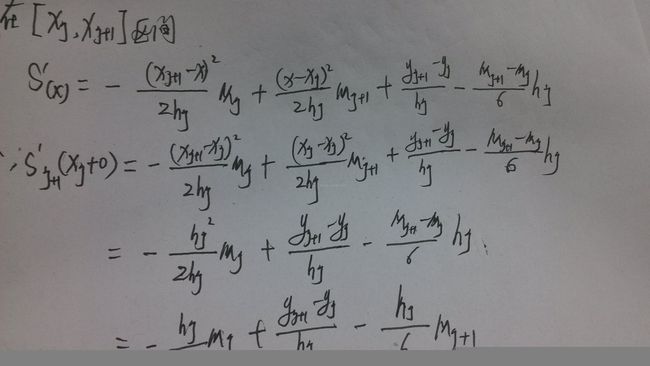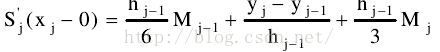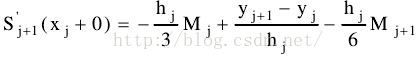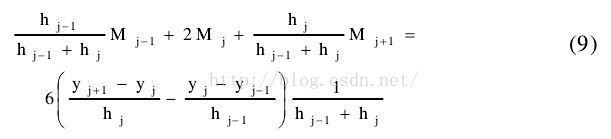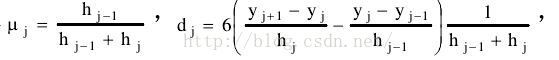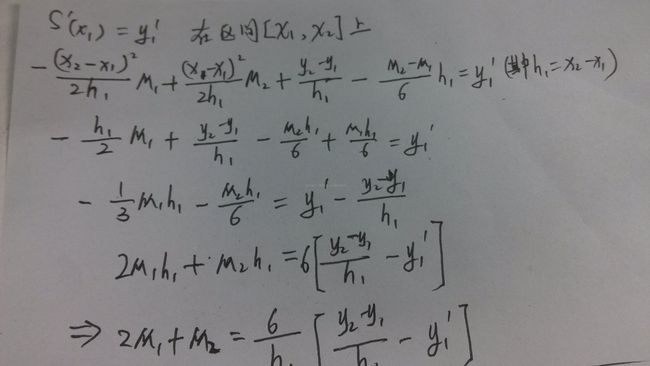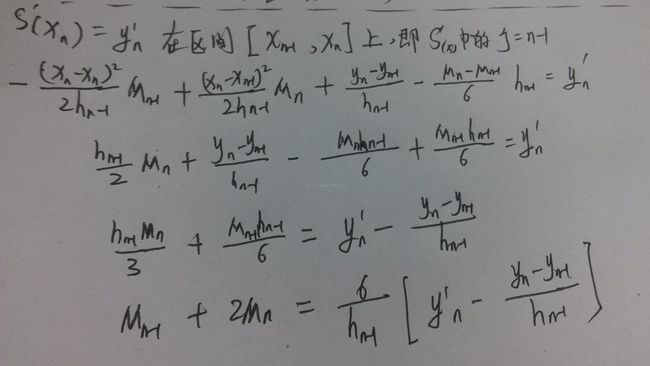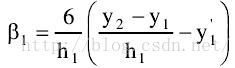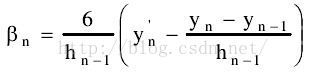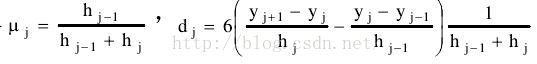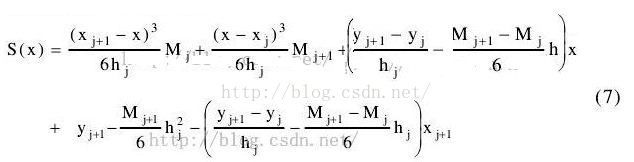Spline(三次样条插值)

关于三次样条插值，计算方法比较复杂，但是静下心来仔细研究也是可以理解的。

本文借鉴文章来源：http://www.cnki.com.cn/Article/CJFDTotal-BGZD200611035.htm

定义：

     简单来说就是给定了一些在区间[a,b]的数据点{x1,x2,x3.....xn}，对应函数值{y1,y2,y3.....yn}，函数在[xj,xj+1]  (j=1,2,...n-1此处根据你的编译器所定，matlab数组下标从1开始的)上有表达式S(x)，且满足下面条件：

1. S(x)是一个三次多项式，在这里设为

2. S(xj)=yj                    （2-1）

3. S(xj-0)=S(xj+0)  (j=2,3....,n-1)这就是保证了在非端点处的其它点连续               (2-2)

4. S'(xj-0)=S'(xj+0) (j=2,3....,n-1)一阶导数连续                              (3-1)

5. S''(xj-0)=S''(xj+0) (j=2,3....,n-1)二阶导数连续                              (3-2)

【注】3 4 5的区间从2开始到n-1是因为两个端点不需要判断是否连续，端点处没连续这一说。

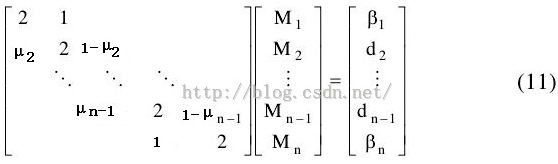
       有一个说法“n个未知数需要n个方程才能确定唯一解”，具体对不对，可以参考线性代数的知识。我们的最终目标是求出每个区间的式(1)或者函数值。 共有n-1个区间，每个区间四个参数aj，bj，cj，dj，那么就总共需要4(n-1)个求未知数。在(2-1)中给出了n个方程，(2-2)(3-1)(3-2)总共给出了3(n-2)个方程，所以依据唯一解方法可知还需要4(n-1)-3(n-1)-n=2个方程。

       对于剩下的两个方程，三次样条插值给出了两个边界约束方程，刚好凑齐两个，并且有三种，可以依照自己的兴趣选择一种便于实现的。

1. 给定了端点处的一阶导数值：S'(x1)=y1'    S'(xn)=yn'

2.给定了端点处的二阶导数值：S''(x1)=y1''    S''(xn)=yn''。自然边界条件：y1''=yn''=0

3.给定了一个周期性条件：如果f(x)是以b-a为周期的函数，在端点处便满足：S'(x1+0)=S'(xn-0)，S''(x1+0)=S''(xn-0)

下面的推导是以边界方程1为例的：

推导过程：

(一) 利用二阶导得到一些式子：

      S(x)为每个区间的三次多项式，那么S''(x)就是一次多项式。假设S''(xj)=Mj，S''(x j+1 )=M j+1 的值已知，那么：

       

其中hj=x j+1 -x j ，然后利用S''(x)求S(x)：

（二）依据S(x)得到一些式子

按照上面的证明可以得到：

其中： h j =x j+1 -x j

依据S(x j )=y j 和S(x j+1 )=y j+1 得到：

解得(求解过程就不写了，简单的二元方程组)

                                     （6-1）

          （6-2）

将Aj和Bj带入S(x)中可以得到S(x)的最终式子：

原文此处应该是有错误，Aj和Bj都没有xj的式子，但是原文的结果中包含。

这里就得到了S(x)的雏形了，xj、x j+1 、hj都是已知的，但是Mj和M j+1 是假设已知的，下面就是求它们了。

（三）利用一阶导数得到一些式子

依据式(7)求出一阶导：

然后为了使在xj处连续平滑，那么在xj处的一阶导必须相等。即要满足S'(xj-0)=s'(xj+0)

即等式坐标表示S(x)在[xj-1,xj]的xj的一阶导值，右边表示[xj,xj+1]的xj一阶导值

其中利用S(x)的表达式可以得到等式左右两边的值：

由上得到两个式子：

由两式相等整理可得：

令：

则μ j M j-1 +2M j +(1-μ j )M j+1 =dj（j=2,3,...,n-1）

(四)带入边界条件

  此处选择边界条件1，即

计算：

结果写为2M 1 +M 2 =β 1

 

结果写为M n-1 +2M n =β n

（五）结果

结合（三）、（四）可以看出所有的n个式子已经齐全：

包括（三）结尾算得μjMj-1+2Mj+(1-μj)Mj+1=dj（j=2,3,...,n-1）的n-2个式子加上(四)得到的两个式子，刚好n个式子.

用矩阵表示出这n个式子即为：

方程中

   

并且hj=xj+1-xj

这样便解出了矩阵M，然后带入S(x)的式子即上面算得：

这样便求得了每一个区间上的S(x)了。

matlab代码：

SplineThree.m

<pre name="code" class="plain">function f = SplineThree(x,y,dy1,dyn,x0)
%x，y为输入的已知点
%x0为待求插值点的横坐标
%dy1,dyn为约束条件，是端点处的一阶导数值
n=length(x);
for j=1:n-1
    h(j)=x(j+1)-x(j);
end

%得到式子右边的结果矩阵
d(1,1)=6*((y(2)-y(1))/h(1)-dy1)/h(1);   %等式(11)的结果矩阵的上端点值
d(n,1)=6*(dyn-(y(n)-y(n-1))/h(n-1))/h(n-1); %等式(11)的结果矩阵的下端点值
for i=2:n-1
    u(i)=h(i-1)/(h(i-1)+h(i));
    d(i,1)=6*((y(i+1)-y(i))/h(i)-(y(i)-y(i-1))/h(i-1))/(h(i-1)+h(i));
end

%得到系数矩阵
A(1,1)=2;
A(1,2)=1;
A(n,n-1)=1;
A(n,n)=2;
for i=2:n-1
    A(i,i-1)=u(i);
    A(i,i)=2;
    A(i,i+1)=1-u(i);
end

%解方程
M=A\d;

format long
syms t;
%得到每个区间的式子
for i=1:n-1
   a(i)=y(i+1)-M(i+1)*h(i)^2/6-((y(i+1)-y(i))/h(i)-(M(i+1)-M(i))*h(i)/6)*x(i+1);
   b(i)=((y(i+1)-y(i))/h(i)-(M(i+1)-M(i))*h(i)/6)*t;
   c(i)=(t-x(i))^3*M(i+1)/(6*h(i));
   e(i)=(x(i+1)-t)^3*M(i)/(6*h(i));
   f(i)=a(i)+b(i)+c(i)+e(i);
    %f(i)=M(i)*(x(i+1)-t)^3/(6*h(i))+M(i+1)*(t-x(i))^3/(6*h(i))+(y(i)-M(i)*h(i)^2/6)*(x(i+1)-t)/h(i)+(y(i+1)-x(i+1)*h(i)^2/6)*(t-x(i))/h(i);
    % f(i)=((x(j+1)-x)^3)*M(i)/(6*h(i))+((x-x(i))^3)*M(i+1)/(6*h(i))+(y(i)-M(i)*(h(i)^2)/6)*((x(i+1)-x)/h(i))+(y(i+1)-(M(i+1)*(h(i)^2)/6))*((x-x(i))/h(i));
end

%化简
 f=collect(f);
 f=vpa(f,6);

 
if(nargin==5)
   nn=length(x0);
for i=1:nn
    for j=1:n-1
        if(x0(i)>=x(j)&x0(i)<=x(j+1))
             yynum(i)=subs(f(j),'t',x0(i));   %计算插值点的函数值.subs是替换函数，把x0用t替换
        end
    end
end   
f=yynum;
else
    f=collect(f);          %将插值多项式展开
    f=vpa(f,6);            %将插值多项式的系数化成6位精度的小数
end
end

SplineThree.m

<pre name="code" class="plain">% x=[-1.5 0 1 2];
% y=[0.125 -1 1 9];
% dy1=0.75;
% dyn=14;
% x0=1.5;
% answer=SplineThree(x,y,dy1,dyn);
% 
% X=[-1.5 0 1 2];
% Y=[0.125 -1 1 9];
% dY=[0.75 14]
% m=5;
% spline3(X,Y,dY,x0,m)

X=0:2*pi;
Y=sin(X);
dY=[1,1];
dy1=1;
dyn=1;
xx=0:0.5:6;
m=5;
% for i=1:length(xx)
% spline3(X,Y,dY,xx,m);
% end
yy=SplineThree(X,Y,dy1,dyn,xx);
plot(xx,yy,'r')