JAVA SkipList 跳表 的原理和使用例子
跳表的原理与特点
跳跃链表是一种随机化数据结构,基于并联的链表,其效率可比拟于二叉查找树(对于大多数操作需要O(log n)平均时间),并且对并发算法友好。
基本上,跳跃列表是对有序的链表增加上附加的前进链接,增加是以随机化的方式进行的,所以在列表中的查找可以快速的跳过部分列表(因此得名)。
所有操作都以对数随机化的时间进行。
跳跃列表是按层建造的。底层是一个普通的有序链表。每个更高层都充当下面列表的"快速跑道",这里在层 i 中的元素按某个固定的概率 p 出现在层 i+1 中。
平均起来,每个元素都在 1/(1-p) 个列表中出现,而最高层的元素(通常是在跳跃列表前端的一个特殊的头元素)在 O(log1/pn) 个列表中出现。
要查找一个目标元素,起步于头元素和顶层列表,并沿着每个链表搜索,直到到达小于或的等于目标的最后一个元素。
通过跟踪起自目标直到到达在更高列表中出现的元素的反向查找路径,在每个链表中预期的步数显而易见是 1/p。所以查找的总体代价是 O(log1/p n / p),
当p 是常数时是 O(logn)。通过选择不同p 值,就可以在查找代价和存储代价之间作出权衡。
插入和删除的实现非常像相应的链表操作,除了"高层"元素必须在多个链表中插入或删除之外。
跳跃列表不像某些传统平衡树数据结构那样提供绝对的最坏情况性能保证,因为用来建造跳跃列表的扔硬币方法总有可能(尽管概率很小)生成一个糟糕的不平衡结构。
但是在实际中它工作的很好,随机化平衡方案比在平衡二叉查找树中用的确定性平衡方案容易实现。跳跃列表在并行计算中也很有用,
这里的插入可以在跳跃列表不同的部分并行的进行,而不用全局的数据结构重新平衡。
跳跃表的应用
Skip list(跳表)是一种可以代替平衡树的数据结构,默认是按照Key值升序的。Skip list让已排序的数据分布在多层链表中,以0-1随机数决定一个数据的向上攀升与否,通过“空间来换取时间”的一个算法,在每个节点中增加了向前的指针,在插入、删除、查找时可以忽略一些不可能涉及到的结点,从而提高了效率。
在Java的API中已经有了实现:分别是
1: ConcurrentSkipListMap. 在功能上对应HashTable、HashMap、TreeMap。 在并发环境下,Java也提供ConcurrentHashMap这样的类来完成hashmap功能。
2: ConcurrentSkipListSet . 在功能上对应HashSet.
确切来说,SkipList更像Java中的TreeMap。TreeMap基于红黑树(一种自平衡二叉查找树)实现的,时间复杂度平均能达到O(log n),TreeMap输出是有序的,ConcurrentSkipListMap和ConcurrentSkipListSet 输出也是有序的(本博测试过)。下例的输出是从小到大,有序的。
package MyMap;
import java.util.*;
import java.util.concurrent.*;
/*
* 跳表(SkipList)这种数据结构算是以前比较少听说过,它所实现的功能与红黑树,AVL树都差不太多,说白了就是一种基于排序的索引结构,
* 它的统计效率与红黑树差不多,但是它的原理,实现难度以及编程难度要比红黑树简单。
* 另外它还有一个平衡的树形索引机构没有的好处,这也是引导自己了解跳表这种数据结构的原因,就是在并发环境下其表现很好.
* 这里可以想象,在没有了解SkipList这种数据结构之前,如果要在并发环境下构造基于排序的索引结构,那么也就红黑树是一种比较好的选择了,
* 但是它的平衡操作要求对整个树形结构的锁定,因此在并发环境下性能和伸缩性并不好.
* 在Java中,skiplist提供了两种:
* ConcurrentSkipListMap 和 ConcurrentSkipListSet
* 两者都是按自然排序输出。
*/
public class SkipListDemo {
public static void skipListMapshow(){
Map<Integer,String> map= new ConcurrentSkipListMap<>();
map.put(1, "1");
map.put(23, "23");
map.put(3, "3");
map.put(2, "2");
/*输出是有序的,从小到大。
* output
* 1
* 2
* 3
* 23
*
*/
for(Integer key : map.keySet()){
System.out.println(map.get(key));
}
}
public static void skipListSetshow(){
Set<Integer> mset= new ConcurrentSkipListSet<>();
mset.add(1);
mset.add(21);
mset.add(6);
mset.add(2);
//输出是有序的,从小到大。
//skipListSet result=[1, 2, 6, 21]
System.out.println("ConcurrentSkipListSet result="+mset);
Set<String> myset = new ConcurrentSkipListSet<>();
System.out.println(myset.add("abc"));
System.out.println(myset.add("fgi"));
System.out.println(myset.add("def"));
System.out.println(myset.add("Abc"));
/*
* 输出是有序的:ConcurrentSkipListSet contains=[Abc, abc, def, fgi]
*/
System.out.println("ConcurrentSkipListSet contains="+myset);
}
}
输出结果:
1
2
3
23
ConcurrentSkipListSet result=[1, 2, 6, 21]
true
true
true
true
ConcurrentSkipListSet contains=[Abc, abc, def, fgi]
HashMap是基于散列表实现的,时间复杂度平均能达到O(1)。ConcurrentSkipListMap是基于跳表实现的,时间复杂度平均能达到O(log n)。
Skip list的性质
(1) 由很多层结构组成,level是通过一定的概率随机产生的。
(2) 每一层都是一个有序的链表,默认是升序
(3) 最底层(Level 1)的链表包含所有元素。
(4) 如果一个元素出现在Level i 的链表中,则它在Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
Ø ConcurrentSkipListMap具有Skip list的性质 ,并且适用于大规模数据的并发访问。多个线程可以安全地并发执行插入、移除、更新和访问操作。与其他有锁机制的数据结构在巨大的压力下相比有优势。
Ø TreeMap插入数据时平衡树采用严格的旋转(比如平衡二叉树有左旋右旋)来保证平衡,因此Skip list比较容易实现,而且相比平衡树有着较高的运行效率。
为什么选择跳表
目前经常使用的平衡数据结构有:B树,红黑树,AVL树,Splay Tree, Treep等。想象一下,给你一张草稿纸,一只笔,一个编辑器,你能立即实现一颗红黑树,
或者AVL树出来吗? 很难吧,这需要时间,要考虑很多细节,要参考一堆算法与数据结构之类的树,
还要参考网上的代码,相当麻烦。
用跳表吧,跳表是一种随机化的数据结构,目前开源软件 Redis 和 LevelDB 都有用到它,它的效率和红黑树以及 AVL 树不相上下,但跳表的原理相当简单,
只要你能熟练操作链表,就能轻松实现一个 SkipList。
有序表的搜索
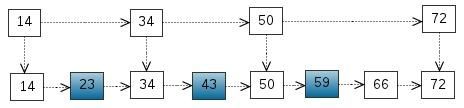
考虑一个有序表:
从该有序表中搜索元素 < 23, 43, 59 > ,需要比较的次数分别为 < 2, 4, 6 >,总共比较的次数
为 2 + 4 + 6 = 12 次。有没有优化的算法吗? 链表是有序的,但不能使用二分查找。类似二叉
搜索树,我们把一些节点提取出来,作为索引。得到如下结构:
这里我们把 < 14, 34, 50, 72 > 提取出来作为一级索引,这样搜索的时候就可以减少比较次数了。
我们还可以再从一级索引提取一些元素出来,作为二级索引,变成如下结构:
这里元素不多,体现不出优势,如果元素足够多,这种索引结构就能体现出优势来了。
这基本上就是跳表的核心思想,其实也是一种通过“空间来换取时间”的一个算法,通过在每个节点中增加了向前的指针,从而提升查找的效率。
跳表
下面的结构是就是跳表:
其中 -1 表示 INT_MIN, 链表的最小值,1 表示 INT_MAX,链表的最大值。
跳表具有如下性质:
(1) 由很多层结构组成
(2) 每一层都是一个有序的链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 如果一个元素出现在 Level i 的链表中,则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针,一个指向同一链表中的下一个元素,一个指向下面一层的元素。
跳表的搜索
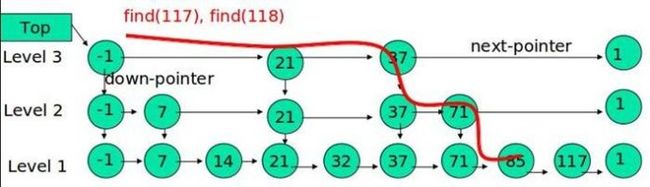
例子:查找元素 117
(1) 比较 21, 比 21 大,往后面找
(2) 比较 37, 比 37大,比链表最大值小,从 37 的下面一层开始找
(3) 比较 71, 比 71 大,比链表最大值小,从 71 的下面一层开始找
(4) 比较 85, 比 85 大,从后面找
(5) 比较 117, 等于 117, 找到了节点。
具体的搜索算法如下:
C代码 ![]()
1.
3. find(x)
4. {
5. p = top;
6. while (1) {
7. while (p->next->key < x)
8. p = p->next;
9. if (p->down == NULL)
10. return p->next;
11. p = p->down;
12. }
13. }
跳表的插入
先确定该元素要占据的层数 K(采用丢硬币的方式,这完全是随机的)
然后在 Level 1 ... Level K 各个层的链表都插入元素。
例子:插入 119, K = 2
如果 K 大于链表的层数,则要添加新的层。
例子:插入 119, K = 4
丢硬币决定 K
插入元素的时候,元素所占有的层数完全是随机的,通过一下随机算法产生:
C代码 ![]()
1. int random_level()
2. {
3. K = 1;
4.
5. while (random(0,1))
6. K++;
7.
8. return K;
9. }
相当与做一次丢硬币的实验,如果遇到正面,继续丢,遇到反面,则停止,
用实验中丢硬币的次数 K 作为元素占有的层数。显然随机变量 K 满足参数为 p = 1/2 的几何分布,
K 的期望值 E[K] = 1/p = 2. 就是说,各个元素的层数,期望值是 2 层。
跳表的高度。
n 个元素的跳表,每个元素插入的时候都要做一次实验,用来决定元素占据的层数 K,
跳表的高度等于这 n 次实验中产生的最大 K,待续。。。
跳表的空间复杂度分析
根据上面的分析,每个元素的期望高度为 2, 一个大小为 n 的跳表,其节点数目的
期望值是 2n。
跳表的删除
在各个层中找到包含 x 的节点,使用标准的 delete from list 方法删除该节点。
例子:删除 71