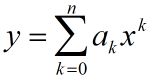《算法导论》系列课后思考题之-第二章《算法入门》

2-1 在合并排序中对小数组采用插入排序

      由题意可知，程序的设计如下所示：

#include "stdafx.h"
#include <string.h>
#include <iostream>
using namespace std;

void Merge(int* arr, int head, int mid, int tail);
void InsertSort(int* arr, int k, int head, int tail) // 进行k个大小的数组插入排序
{
	if (head + k - 1< tail) {
		int mid = (head + tail)	/ 2;
		InsertSort(arr, k, head, mid);
		InsertSort(arr, k, mid + 1, tail);
		Merge(arr, head, mid, tail);
	}
	else {
		int key, i, j;
		for (i =  head + 1; i <= tail; i++)
		{
			key = arr[i];
			for (j = i - 1; j >= head && key < arr[j]; j--)
				arr[j+1] = arr[j];
			arr[j + 1] = key;

		}
	}
}

void Merge(int* arr, int head, int mid, int tail)
{
	int n1 = mid - head + 1;
	int n2 = tail - mid;
	int* arr1 = new int[n1 + 1];
	int* arr2 = new int[n2 + 1];
	int i, j, k;

	for(int i = 0; i < n1; i++)
		arr1[i] = arr[head + i];
	for(int i = 0; i < n2; i++)
		arr2[i] = arr[mid + 1 + i];

	arr1[n1] = 1000000000;	//哨兵
	arr2[n2] = arr1[n1];

	i = j = 0;
	k = head;
	while(k <= tail) {
		if (arr1[i] <= arr2[j]) {
			arr[k] = arr1[i];
			i++;
			k++;
		}
		else {
			arr[k] = arr2[j];
			j++;
			k++;
		}
	}
	delete[] arr1;
	delete[] arr2;
}

测试后通过。关键代码是InsertSort函数中的“if (head + k - 1< tail)”，这句决定了可以进行多大范围的插入排序。

那么a).每次插入排序最坏情况下显然为O(n^2)，共进行了n/k次插入排序，显然是在O(nk)时间内完成；

b).由于有n/k个子列表，那么共有log(n/k)+1层。每一层的代价是O(n)，因此总共的时间复杂度为O(nlog(n/k))；

c).标准的合并算法时间复杂度为O(nlog(n))，要使修改后的算法具有与标准合并排序算法一样的渐进运行时间，k的最大渐进值是logn，原来时间复杂度为O(nk + nlog(n/k))，现在变为了O(nlogn + nlog(n/logn))，忽略nlog(n/logn)的影响，这样即为O(nlogn)；

d).在满足插入排序比合并排序更快的前提下，k取最大值。

 

2-2 冒泡排序算法的正确性

a)A'中的值全部来自A；

b)起始：A数组的初始状态为A[1]、A[2]、A[3]、……A[n]，对于for的第一个元素，即j=n，A[n]来说，其元素本身对于只有该元素的数组来说已排好序；

保持：当i=k时，对于j = k-1个元素来说，已经是排好的最小的k-1个元素，当j=n时，A[n]需要与A[n-1]比较，当j为k+1时，A[k+1]是A[n]~A[k]中次小或者最小的数，交换后A[k]变为第k个最小的元素，此时也已经排好序；

终止：当i=n-1时，我们已经排好n-2个最小的元素，j=n时，A[j]只需和A[j-1]比较一次即排好序。

c)起始：A'数组的初始状态为空

保持：若i=k，则A'[1]、A'[2]、……A'[i-1]已经排好序，由b)可知，排序后A'[1]、A'[2]、……、A‘[i]为排好序的；

终止：i=n时，所有数都已经排好序了。

d)O(n^2)，最坏情况下也是Σ（n-i）

 

2-3 霍纳规则的正确性

a)霍纳规则的代码渐进运行时间是n?；

b)朴素多项式？伪代码是：

void Ploynomial()
{
	int t;
	sum = a[0];
	for (i = 1; i < n; i++)
	{
		sum += a[i]*x;
		x *= x;
	}
}

那么运行时间应该是2n吧？与上述相比是2倍时间长度；

c)起始：因为y初始状态为0，i为n，因此在第一轮迭代的开始时有，这时y正好为0；

保持：利用数学归纳法，若i = k+1时，迭代前为，此时成立；那么对于下一轮迭代，i=k，迭代前有

，此时

，必然成立。

终止：终止时i=-1，那么此时，与原多项式相同，证明成立

2-4 逆序对

a)列出5个逆序对：（2,1），（3,1），（8,6），（8,1），（6,1）。so easy~~

b)怎样的数组含有最多的逆序对？它们包含多少个逆序对？

从大到小排列，为（n,n-1,n-2,...,1），共（n-1）n/2个。

c)相等。插入排序的思想是，若已经排好序的数为n，待排序的数为第n+1个，需与第n个数比较，若逆序，交换后，再与第n-1个数比较；若不逆序，停止比较。否则直到第1个数与当前数比较完毕。比较的次数和逆序的次数是一样多的。

d) 算法如下所示：

#include "stdafx.h"

int count = 0;

void Merge(int *arr, int head, int mid, int tail)
{
	int n1 = mid - head + 1;
	int n2 = tail - mid;

	int* arr1 = new int[n1 + 1];
	int* arr2 = new int[n2 + 1];

	int i, j, k;
	for (i = 0; i < n1; i++)
		arr1[i] = arr[head + i];
	for (i = 0; i < n2; i++)
		arr2[i] = arr[mid + i + 1];

	arr1[n1] = arr2[n2] = 1000000000;

	i = j = 0;
	k = head;
	while (k <= tail) {
		if (arr1[i] < arr2[j]) {
			arr[k] = arr1[i];
			i++;
		}
		else {
			arr[k] = arr2[j];
			count++;
			j++;
		}
		k++;
	}
	delete [] arr1;
	delete [] arr2;
}

void MergeSort(int* arr, int head, int tail)
{
	if (head < tail)
	{
		int mid = (head + tail) / 2;
		MergeSort(arr, head, mid);
		MergeSort(arr, mid + 1, tail);
		Merge(arr, head, mid, tail);
	}
	 
}

int _tmain(int argc, _TCHAR* argv[])
{
	int a[5] = {2,3,8,6,1};
	MergeSort(a, 0, 4);
	printf("%d", count);
	return 0;
}

部分参考http://blog.csdn.net/powerrock/article/details/2478700