Dijkstra算法求解最短路径

Dijkstra算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

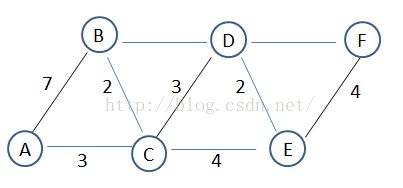
假设存在无向网（如下所示），希望计算从点A到其他各个顶点的最短距离

令R = {}表示已计算最短路径的点的集合，S ={A,B,C,D,E,F}表示还未计算的点的集合。数组closeDis表示起点到其他任何顶点的最短距离;数组prePoint表示该点的最短路径所经过的上一个点。取A作为起始结点，然后寻找离A最近的顶点C作为新的拓展结点并加入到已求解集合，从A－>C的路径开始寻找，若到其他顶点的距离小于旧记录，则更新并保存最近的距离，接着寻找离C最近的顶点B作为新的拓展结点，不断循环，直到所有的顶点都加入到已求解集合里，程序结束。

下边通过手工寻找最短路径来理解算法的运行过程

有了prePoint数组，就可以通过迭代不断寻找上一个结节，直到找到起点位置，从而可得起点到任何一个顶点的完整路径。以寻找点F的完整路径为例，由 prePoint={0,2, 0, 2,2, 3}可知，F的上一个结点为D，而D的上一个结点为C,C的上一个结点为A，故F的完整路径为A->C->D->F。

完整的源代码如下

import java.util.HashSet;
import java.util.LinkedList;
import java.util.Set;

public class DijkstraShortestPath {
	
	private static final int MIN_DIS = 0;
	private static final int MAX_DIS = 99;
	// 图的邻接矩阵
	int[][] matrix;
	// 起始点
	int startIndex;
	// 保存起始点到其它点的最短距离
	int[] closeDis;
	//保存最优路径所经过的上一个点
	int[] prePoint;	
	// 用来存放已经找到最短路径的点的集合
	Set<Integer> foundSet = new HashSet<Integer>();

	public DijkstraShortestPath(int[][] matrix, int start) {
		this.matrix = matrix;
		this.startIndex = start;
		this.closeDis = new int[matrix.length];
		this.prePoint = new int[matrix.length];
	}

	/**
	 *  算法的核心代码，寻找最短路径
	 */
	public void findPath() {
		// 把邻接矩阵第startIndex行的数据作为初始值
		for (int i = 0; i < matrix.length; i++) {
			closeDis[i] = matrix[startIndex][i];
		}
		
		//从起点开始找，将起点作为当前拓展结点
		int expandNode = startIndex;
		foundSet.add(startIndex);
		
		while (foundSet.size() != matrix.length) {
			int nearestNode = findNearNode(expandNode);//寻找离拓展结点最近的结点
			//遍历各个顶点，如果发现距起点更小的距离，则更新并保存
			for (int i = 0; i < matrix.length; i++) {
				if (!foundSet.contains(i) && matrix[nearestNode][i] != MAX_DIS
						&& matrix[nearestNode][i] + closeDis[nearestNode]  < closeDis[i] ){
					closeDis[i] = matrix[nearestNode][i] + closeDis[nearestNode];
					prePoint[i] = nearestNode;
				}
			}
			// 放入foundSet
			foundSet.add(nearestNode);
			expandNode = nearestNode;
		}
	}

	/**
	 *  打印从起始点到所有点的最短距离
	 */
	public void printDistance(){
		System.err.println("使用Dijkstra寻找最短路径");
		for(int i=0;i<closeDis.length;i++){
			System.err.println("从"+renameNode(startIndex)+"到"+renameNode(i)+"，总长度为"+closeDis[i]+"，路径为"+printPath(i));
		}
	}
	
	/**
	 *  返回当前最小距离的点(必须不包含在findedSet中)
	 */
	private int findNearNode(int nodeIndex) {
		int min = Integer.MAX_VALUE;
		int minIndex = -1;
		
		int[] subMatrix = matrix[nodeIndex];
		for(int i=0;i<subMatrix.length;i++){
			if(!foundSet.contains(i)  && subMatrix[i] < min){
				min = subMatrix[i];
				minIndex = i;
			}
		}
		
		return minIndex;
	}

	public static void main(String[] args) {
		int[][] weightMatrix = new int[][] { { MIN_DIS,7,3, MAX_DIS,MAX_DIS,MAX_DIS}, { 7,MIN_DIS,2,4,MAX_DIS,MAX_DIS},
				{3,2,MIN_DIS,3,4,MAX_DIS}, { MAX_DIS,4,3,MIN_DIS,2,3},
				{MAX_DIS,MAX_DIS,4,2,MIN_DIS,4 }, { MAX_DIS,MAX_DIS,MAX_DIS,2,4,MIN_DIS}};
		System.out.println("图的邻接矩阵为");
		printAdjacentMatrix(weightMatrix);		
		DijkstraShortestPath path = new DijkstraShortestPath(weightMatrix, 0);
		path.findPath();
		path.printDistance();

	}
	
	/**
	 *  打印邻接矩阵
	 */
	private static  void printAdjacentMatrix(int[][] inputMatrix){
		final int nodeCount = inputMatrix.length;
		for(int i=0;i<nodeCount;i++){
			for(int j=0;j<nodeCount;j++){
				System.out.print(inputMatrix[i][j]+" "+"\t\t");
			}
			System.out.println();
		}
	}
	
	/**
	 *  打印从起点到终点的完整路径
	 */
	private String printPath(int nodeIndex){
		int firstIndex = nodeIndex;
		LinkedList<String> paths = new LinkedList<String>();
		
		while(firstIndex > 0){//不断寻找上一个结点，直到起点
			paths.offerFirst(renameNode(firstIndex));//从队首加入元素
			firstIndex = prePoint[firstIndex]; 
		}
		paths.offerFirst(renameNode(startIndex));//加上起点位置
		return paths.toString();
	}
	
	private String renameNode(int index){
		char c =(char) (97+index);  //97为字符'a'的ascii值
		return String.valueOf(c) ;
	}
	
}

程序结果如下