Poj_3744 解题报告

原题我就不提供了, 大家可以自己上www.POJ.org搜索.

大概题意 :

小明要通过一条"地雷之路".路上有好多个地雷, 而小明现在站在路的开端(1号位置), 小明有P的概率向前移动一步, 有(1-P)的概率向前移动两步, 问小明能安全通过这条路的概率.

输入格式:

1 . 输入多组数据, 以EOF结束

2 . 每组数据包括两行, 第一行输入N,P , 分别表示地雷数目和走一步的概率;

第二行输入N个正整数, 表示地雷的位置;

输出格式:

每组数据的结果占据一行, 表示安全通过的概率, 以7位浮点数表示

示例输入:

1 0.5

2

2 0.5

2 4

示例输出:

0.5000000

0.2500000

解题思路 :

先将题目转化为概率DP(动态规划)的问题, 再优化为矩阵乘法问题.

1 . 使用最小优先队列来记录路上所有地雷的位置.

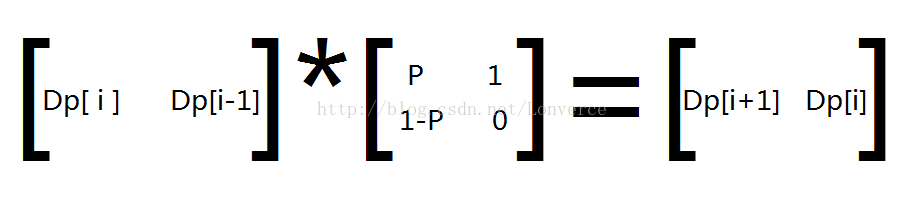
2 . 定义Dp[ i ]表示小明能安全到达第i号位置的概率.

3 . 状态转移方程 :

Dp[ i ] = P*Dp[i-1] + (1-P)Dp[i-2] ;  // 第 i 号位置没有地雷

Dp[ i ] = 0;        // 第 i 号位置有地雷

4 . 矩阵表达式:

5 . 当 i 号位置存在地雷时 , 设Dp[ i ] = 0;

6 . 当有两个连续位置存在地雷时, 最后结果必然为0

有了上述的理论基础, 我们可以给出如下代码:

#include <iostream>
#include <vector>
#include <queue>
#include <iomanip>
#include <functional>
using namespace std;

typedef unsigned int uint;
typedef uint SizeType;
typedef uint IndexType;
typedef double ValueType;
typedef vector<ValueType> RowType;
typedef vector<RowType> ContainerType;
// ...矩阵类的实现 
class Matrix{
	public:
		Matrix( SizeType nRow, SizeType nCol, ValueType initVal )
			:m_mtx( *(new ContainerType( nRow, RowType(nCol,initVal) )) ){}
		Matrix( const Matrix& right ):m_mtx(*(new ContainerType( right.m_mtx ))){}
		~Matrix(){ delete &m_mtx; }
		inline SizeType GetRow()const{ return m_mtx.size(); }
		inline SizeType GetCol()const{ return GetRow()?m_mtx[0].size():0;}
		inline const ValueType& operator()( IndexType row, IndexType col )const{ return m_mtx[row][col]; }
		inline ValueType& operator()( IndexType row, IndexType col ){ return m_mtx[row][col]; }
		const Matrix& operator=( const Matrix& right ){ return (m_mtx = right.m_mtx,*this);}
		const Matrix operator*( const Matrix& right )const{
			Matrix Res( GetRow(), right.GetCol(), 0);
			if( GetCol()==right.GetRow()){
				const Matrix& left = *this;
				SizeType row = GetRow(), col = right.GetCol(),end = GetCol();
				for( IndexType i = 0; i < row; ++i) 
					for( IndexType j = 0; j < col; ++j)
						for( IndexType t = 0; t < end; ++t )
							Res(i,j) += left(i,t)*right(t,j);
			}
			return Res;
		}// ...矩阵乘法 
		const Matrix& operator*=( const Matrix& right ){ return *this = *this*right; }
		static Matrix GetIdentity( SizeType nDimension ){
			Matrix Id( nDimension, nDimension, 0);
			for( IndexType i = 0; i < nDimension; ++i ) Id(i,i) = 1;
			return Id;
		}// ...获得n阶单位矩阵 
		const Matrix operator^( uint N )const{
			Matrix Res = GetIdentity( GetRow() ), Mul(*this);
			while( N ){
				if( N&1 ) Res *= Mul;
				Mul *= Mul;
				N>>=1;
			}
			return Res;
		}// ...矩阵快速幂 
		const Matrix& operator^=( uint N ){	return *this = *this^N; }
	protected:
		ContainerType &m_mtx;	//...矩阵容器 
};

// ...数据集采用优先队列实现( 升序排序 ) 
typedef priority_queue< IndexType,vector<IndexType>,greater<IndexType> > DataSetType; 
typedef queue< ValueType >	ResultSetType;	// ...结果集采用普通队列实现 

void Calculate( DataSetType& DSet, ResultSetType& RSet,ValueType P){
	Matrix Base(1,2,0);	// ...基本概率矩阵: Base = [ dp(i), dp(i-1) ];
	Matrix Ext(2,2,0);	// ...线性组合描述矩阵 : dp(i+1) = dp(i)*P + dp(i-1)*(1-P) ;
	uint N = 0,preN = 0,from = 1;	// ...当前死亡位置, 前一个死亡位置, 开始位置 
	Ext(0,0) = P;		//		  |-	    -|
	Ext(0,1) = 1.0;		//		  | P   ,  1 |
	Ext(1,0) = 1-P;		//	Ext =     | 	     |
	Ext(1,1) = 0;		//		  | 1-P ,  0 |
	Base(0,0) = 1;		//		  |-	    -|
	while( !DSet.empty() ){
		Matrix M(Ext);	
		preN = N;		// ...记录前一次的死亡位置 
		N = DSet.top();	// ...获取下一个死亡位置 
		DSet.pop();	
		if( preN+1 == N ){ 	// ...如存在两个连续的死亡位置, 则必然无法成功渡过 
			RSet.push( 0.0 );
			while( !DSet.empty() ) DSet.pop();
			return;
		}		
		M^=(N-from);	// ...从上一个位置 到 下一个死亡位置, 需前进N-from步,即N-from次线性组合 
		Base*=M;		// ...表示从起始位置Base,经过矩阵M描述的线性变换 
		Base(0,0) = 0.0;// ...那是一个死亡位置, 安全到达的概率必然为0 
		from = N;
	}
	RSet.push( Base(0,1)*Ext(1,0) );
}
int main(int argc, char** argv) 
{
	ResultSetType RSet;		// ...结果集合 
	DataSetType DSet;		// ...数据集合 
	uint N,data;
	ValueType P;
	while(cin >> N >> P){
		for( uint i = 0; i < N; ++i) {
			cin >> data;
			DSet.push( data );
		}
		Calculate( DSet, RSet , P);
	}
	while( !RSet.empty() ){
		cout << fixed << setprecision(7) << RSet.front() << endl;
		RSet.pop();
	}
	return 0;
}