BZOJ4503 两个串

orz xuruifan发discuss问题解……

题解可以看这题discuss

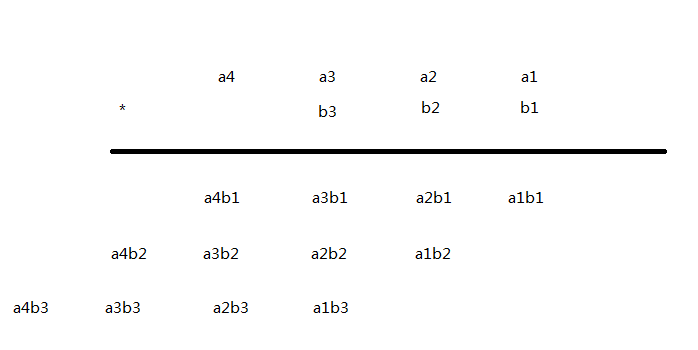
至于如何用FFT算卷积，我们写一下高精乘，用字母代表每一位，发现乘完了其实就是卷积的形式

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<iomanip>
#include<cstring>
#include<cmath>
#include<ctime>
#include<vector>
#include<stack>
#include<queue>
#include<set>
#include<bitset>
#include<map>
using namespace std;
#define MAXN 400010
#define MAXM 10010
#define INF 1000000000
#define MOD 1000000007
#define ll long long
#define eps 1e-8
const double pai=acos(-1);
struct cl{
	double x;
	double y;
	cl(){
		
	}
	cl(double _x,double _y){
		x=_x;
		y=_y;
	}
	cl operator =(double x){
		this->x=x;
		this->y=0;
		return *this;
	}
	friend cl operator +(cl x,cl y){
		return cl(x.x+y.x,x.y+y.y);
	}
	friend cl operator -(cl x,cl y){
		return cl(x.x-y.x,x.y-y.y);
	}
	friend cl operator /(cl x,double y){
		return cl(x.x/y,x.y/y);
	}
	friend cl operator *(cl x,double y){
		return cl(x.x*y,x.y*y);
	}
	friend cl operator *(cl x,cl y){
		return cl(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x);
	}
};
char S[MAXN],T[MAXN];
int s[MAXN],t[MAXN];
cl a1[MAXN],a2[MAXN],a3[MAXN],b1[MAXN],b2[MAXN],b3[MAXN],a[MAXN],b[MAXN],ans[MAXN];
int n,m;
int L;
int R[MAXN];
int ANS;
void fft(cl *x,int y){
    int i,j,k;
    for(i=0;i<n;i++){
        if(i<R[i]){
            swap(x[i],x[R[i]]);
        }
    }
    for(i=1;i<n;i<<=1){
        cl wn(cos(pai/i),y*sin(pai/i));
        for(j=0;j<n;j+=(i<<1)){
            cl w(1,0);
            for(k=0;k<i;k++,w=w*wn){
                cl X=x[j+k],Y=w*x[j+k+i];
                x[j+k]=X+Y;
                x[j+k+i]=X-Y;
            }
        }
    }
    if(y==-1){
        for(i=0;i<n;i++){
            x[i].x/=n;
            x[i].y/=n;
        }
    }
}

void FFT(cl *a,cl *b,int f){
	int i;
	fft(a,1);
	fft(b,1);
	for(i=0;i<n;i++){
		a[i]=a[i]*b[i];
	}
	fft(a,-1);
	for(i=0;i<n;i++){
		ans[i]=ans[i]+(a[i]*f);
	}
}
int main(){

	int i;
	scanf("%s%s",S,T);
	n=strlen(S);
	m=strlen(T);
	for(i=1;i<=m/2;i++){
		swap(T[i-1],T[m-i]);
	}
	for(i=0;i<n;i++){
		s[i]=S[i];
		t[i]=T[i];
		if(T[i]=='?'){
			t[i]=0;
		}
		a1[i]=s[i]*s[i]*s[i];
		b1[i]=t[i];
		a2[i]=s[i]*s[i];
		b2[i]=t[i]*t[i];
		a3[i]=s[i];
		b3[i]=t[i]*t[i]*t[i];
	}
	int N=n*2;
	for(n=1;n<=N;n<<=1){
		L++;
	}
	for(i=0;i<n;i++){
		R[i]=(R[i>>1]>>1|((i&1)<<(L-1)));
	}
	FFT(a1,b1,1);
	FFT(a2,b2,-2);
	FFT(a3,b3,1);
	for(i=m-1;i<N/2;i++){
		if(int(ans[i].x+0.1)==0){
			ANS++;
		}
	}
	printf("%d\n",ANS);
	for(i=m-1;i<N/2;i++){
		if(int(ans[i].x+0.1)==0){
			printf("%d\n",i-(m-1));
		}
	}
	return 0;
}

/*

*/