Graph Cutting CF 405E DFS

题目描述：

Little Chris is participating in a graph cutting contest. He’s a pro. The time has come to test his skills to the fullest.

Chris is given a simple undirected connected graph with n vertices (numbered from 1 to n) and m edges. The problem is to cut it into edge-distinct paths of length 2. Formally, Chris has to partition all edges of the graph into pairs in such a way that the edges in a single pair are adjacent and each edge must be contained in exactly one pair.

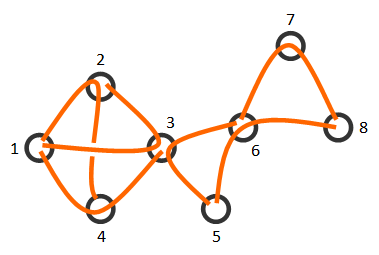
For example, the figure shows a way Chris can cut a graph. The first sample test contains the description of this graph.

You are given a chance to compete with Chris. Find a way to cut the given graph or determine that it is impossible!

输入输出：

Input
The first line of input contains two space-separated integers n and m (1 ≤ n, m ≤ 105), the number of vertices and the number of edges in the graph. The next m lines contain the description of the graph’s edges. The i-th line contains two space-separated integers ai and bi (1 ≤ ai, bi ≤ n; ai ≠ bi), the numbers of the vertices connected by the i-th edge. It is guaranteed that the given graph is simple (without self-loops and multi-edges) and connected.

Note: since the size of the input and output could be very large, don’t use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.

Output
If it is possible to cut the given graph into edge-distinct paths of length 2, output lines. In the i-th line print three space-separated integers xi, yi and zi, the description of the i-th path. The graph should contain this path, i.e., the graph should contain edges (xi, yi) and (yi, zi). Each edge should appear in exactly one path of length 2. If there are multiple solutions, output any of them.

If it is impossible to cut the given graph, print “No solution” (without quotes).

Sample Input
Input

8 12
1 2
2 3
3 4
4 1
1 3
2 4
3 5
3 6
5 6
6 7
6 8
7 8

Output

1 2 4
1 3 2
1 4 3
5 3 6
5 6 8
6 7 8

Input

3 3
1 2
2 3
3 1

Output
No solution
Input

3 2
1 2
2 3

Output

1 2 3

题目描述：

一个无向图，其中有n个顶点，m条边，要求将此图分割成三个顶点，两条边的若干子图，并且将其三个顶点按次序输出（有多个合理的答案，任意输出其中一种），若无法完全将原图分割，输出’No solution’。

我们将这个无向图改造一下，变成有向图，并对边记录进行DFS，找到每个与这条边相连的边，找到就输出顶点，最后将剩下的顶点‘相连’，输出。
只要m是奇数就无解，是偶数就有解。

代码如下：

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <algorithm>
const int MAXN=100005;
using namespace std;


struct node
{
    int to;
    int next;
} map[MAXN*2];
int m,n;
int head[MAXN];
int mk[MAXN];

void addedge(int u,int v,int num)//添加边
{
    map[num].to=v;
    map[num].next=head[u];
    head[u]=num;//给每个顶点作上标记 为1、2、3、、
}

bool dfs(int u,int pre)//深搜
{
    mk[u]=1;
    int pp[2],cnt=0;
    for(int i=head[u]; i!=-1; i=map[i].next)
    {
        int v=map[i].to;
        if(mk[v]==0)
        {
            if(!dfs(v,u)) pp[cnt++]=v;
        }
        else if(mk[v]==1 && v!=pre)
        {
            pp[cnt++]=v;
        }
        if(cnt==2)
        {
            cnt=0;
            printf("%d %d %d\n",pp[0],u,pp[1]);
        }
    }
    mk[u]=2;
    if(cnt)
    {
        printf("%d %d %d\n",pre,u,pp[0]);
        return 1;
    }
    return 0;
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        memset(head,-1,sizeof(head));
        memset(mk,0,sizeof(mk));
        for(int i=0; i<m; i++)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            addedge(u,v,2*i);//添加边，并做标记
            addedge(v,u,2*i+1);
        }
        if (m&1) printf("No solution\n");
        else dfs(1,-1);
    }
    return 0;
}