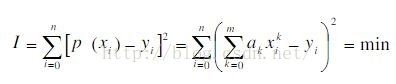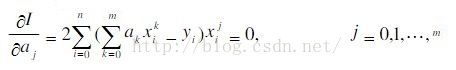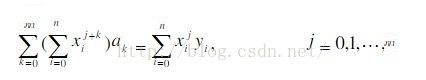多项式曲线拟合最小二乘法

对给定的试验数据点(xi,yi)(i=1,2,……,n),可以构造m次多项式

数据拟合的最简单的做法就是使误差p(xi)-yi的平方和最小

当前任务就是求一个P(x)使得

从几何意义上讲就是寻求给与定点(xi,yi)距离的平方和最小的曲线y=p(x)，函数p(x)称为拟合函数或者是最小二乘解，求拟合函数p(x)的方法称为曲线拟合的最小二乘法

由极值条件得到

即求得

通过简单运算可以得出系数是下面线性方程组的解。

在matlab中编程实现多项式曲线拟合函数为：LeastSquareDetail

功能：求已知数据点的多项式曲线拟合插值法多项式

调用格式：A=LeastSquareDetail(x,y,m,x0)

其中：x为已知数据点的x坐标向量

      y为已知数据点的y坐标向量

      m为拟合多项式的次数

      A为拟合多项式的系数向量

多项式曲线拟合的matlab实现

LeastSquareDetail<span style="font-family: Arial, Helvetica, sans-serif; background-color: rgb(255, 255, 255);">.m</span>

<pre name="code" class="plain">function f = LeastSquareDetail(x,f,m,x0)
%x代表输入的x的值
%y代表输入的x对应的y值
%m代表拟合的次数
%x0为待求的点的x坐标

format long g
a=length(x);
b=length(f);
if(a~=b)
    disp('xy的维数不相等！！');
end

%求得矩阵A
A=zeros(m+1);
for i=1:m+1
    for j=i:m+1
        if(i==1&&j==1)
            A(i,j)=a;
        else
            for k=1:a
            A(i,j)=A(i,j)+x(k)^(i+j-2);
            end
        end
        A(j,i)=A(i,j);
    end
end

%求得等式右边的矩阵
B=zeros(1,m+1);
for i=1:m+1
    if(i==1)
        for k=1:a
            B(i)=B(i)+f(k);
        end
    else
        for k=1:a
        B(i)=B(i)+x(k)^(i-1)*f(k);
        end
    end
end
B=B';
%求解系数
X=A\B;

%求得到的方程
syms t;
c=length(X);
f=0;
for i=1:c
    f=f+X(i)*t^(i-1);
    f=collect(f);
    f=vpa(f,6);
end

if nargin==4
    f=subs(f,'t',x0);
end

LeastSquareDetail<span style="font-family: Arial, Helvetica, sans-serif; background-color: rgb(255, 255, 255);">Insert.m</span>

<pre name="code" class="plain">% x=[36.9 46.7 63.7 77.8 84.0 87.5];
% y=[181 197 235 270 283 292];
% LeastSquareDetail(x,y,1)

x=0:2*pi;
y=sin(x);
xx=0:0.1:2*pi;
yy=LeastSquareDetail(x,y,3,xx);
plot(x,y,'b',xx,yy,'r')