算法基础 - 线段树
线段树
线段树本身是一个很简单的数据结构,但是因为应用场景不同,所以每个人设计的节点和结构还有存储方式也都不一样。
这造成了结构本身很简单,但是想要学却比较麻烦,先说下存储方式:
树存储方式
- 数组
- 树节点指针
我这里只实现了用树节点指针的方式,数组方式同树节点指针一样,只不过leftchild和rightchild做了下标映射。注意数组越界。
应用场景
- 给定一堆数字,找在这个区间里有多少个数字
- 给定一堆线段(lower, upper),找某个数字在多少个线段中出现过。
这里把两种场景都实现了一下,应该还有其他场景,不过暂时没有实现过,但是大同小异,例如一面墙,有几个矩形挡住了阳光,最后问影子大小,或者漏出的空间大小,都是一样的实现。
树结构
树的机构比较简单,就是类似一个二叉树,然后树节点存放了想要的信息。结构如图所示:
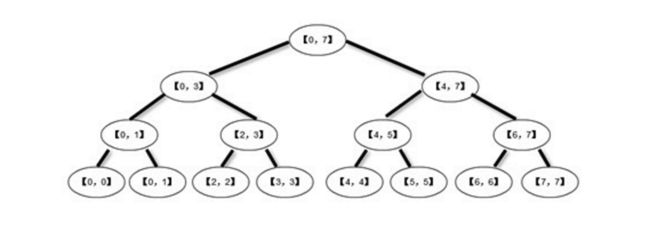
可以看到这棵树,是一个区间为0-7的线段树,这里看到整个区间是连续的,那么不连续可以么?
可以的! 可以建立有序但不连续的线段树,例如 0-5, 6-10这种树。下面实现是通用的。
解释应用1
给定一堆数字,找在这个区间里有多少个数字- 先在线段树中添加数字。
- 每添加一个数字,在路径标记中+1
- 判断给定区间内的数字个数
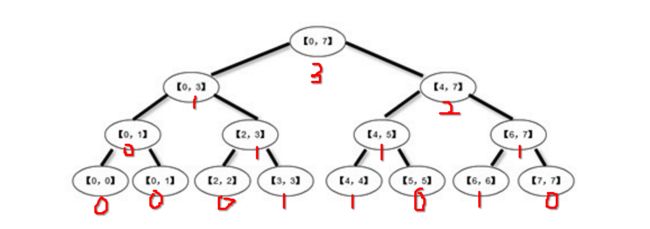
例如上面的线段树添加数字:3,4,6会怎么标记呢?
这就是添加3,4,6三个数字之后的标记结果,看到只要区间内包含了数字,就会+1。
然后判断例如区间[3, 5]之间有多少个数字呢?
- 加入区间大于当前节点的区间,直接返回标记
- 如果遇到区间完全没有重合则直接返回0
- 否则分别到左右子树进行搜索,搜索
[lower, mid]和[mid+1, upper]
如果按照上面的流程进行搜索,则返回的数值是:2。
解释应用2
给定一堆线段(lower, upper),找某个数字在多少个线段中出现过这个是应用1很像,一些区别在于:
- 添加是添加线段,而不是添加数字
- 搜索是搜索包含数字的线段个数,而不是数值个数
- 添加线段的时候,标记的是完全符合的区间,
(lower == min && upper == max),否则继续递归。
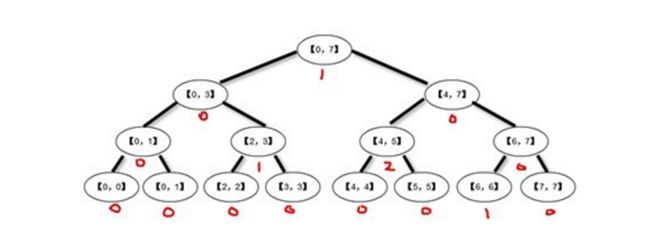
例如上面的树进行区间:[2, 5] [4, 6] [0,7]三个线段的添加,标记会入下图所示:
添加过程
- 判断区间是否完全符合
- 符合直接标记返回,不符合判断区间属于左子树还是右子树
- 属于左子树直接递归到左子树添加,属于右子树到右子树添加
- 如果区间属于左右子树各一部分,则以当前节点的mid为中间,分割区间,递归添加
这个就是添加过程。
获得线段数量
- 加上当前节点的计数,然后递归到属于自己的下一个子树继续加
- 返回结果
是不是很简单!!
代码实现
下面放一下代码实现,这两个场景都写了,所以节点显得稍微臃肿了一点。并且因为写成一个类并不方便答题,所以就写成结构体,函数形式,方便使用吧。
//
// main.cpp
// SegmentTree
//
// Created by Alps on 16/5/1.
// Copyright © 2016年 chen. All rights reserved.
//
#include <iostream>
#include <vector>
using namespace std;
/** * Segement Tree Node struct * countValue : count for value in segment * countSegement : count for segement(lower, upper) * maxValue: max value for the node * minValue: min value for the node */
struct TreeNode{
int countValue;
int countSegment;
int maxValue, minValue;
TreeNode * left;
TreeNode * right;
};
/** * Initial the Segment Tree, keep the num in vector * * @param nums the segmetn number * @param left left loc in vector<int>nums * @param right right loc in vecotr<int>nums * * @return SegmentTree node */
TreeNode * InitSegmentTree(vector<int> nums, int left, int right){
if(left > right) return NULL;
TreeNode * root = new TreeNode();
root->countValue = 0;
root->countSegment = 0;
root->maxValue = nums[right];
root->minValue = nums[left];
root->left = NULL;
root->right = NULL;
if (left == right) {
return root;
}
int mid = (left+right)/2;
root->left = InitSegmentTree(nums, left, mid);
root->right = InitSegmentTree(nums, mid+1, right);
return root;
}
/** * add a value into the segment tree * * @param value add value * @param root segment tree root node * * @return add success : true, fail : false; */
bool add(int value, TreeNode * root){
if (root == NULL) {
return false;
}
if (value < root->minValue || value > root->maxValue) {
return false;
}
root->countValue++;
if (root->left && value <= root->left->maxValue) {
return add(value, root->left);
}else if(root->right && value >= root->right->minValue){
return add(value, root->right);
}
return true;
}
/** * get the number loc in segment tree * * @param lower segment lower number for search * @param upper segment upper number for search * @param root segment tree root node * * @return the count of number in segment tree between lower and upper */
int getCount(int lower, int upper, TreeNode * root){
if (root == NULL) {
return 0;
}
if (lower <= root->minValue && upper >= root->maxValue) {
return root->countValue;
}
if (lower > root->maxValue || upper < root->minValue) {
return 0;
}
int leftCount = root->left ? getCount(lower, upper, root->left) : 0 ;
int rightCount = root->right ? getCount(lower, upper, root->right) : 0;
return leftCount + rightCount;
}
/** * add a segment to segment tree * * @param lower segment lower number for add * @param upper segment upper number for add * @param root setment tree root node * * @return add if success true:false; */
bool addSegment(int lower, int upper, TreeNode *root){
if (root == NULL) {
return false;
}
if (lower < root->minValue || upper > root->maxValue) {
return false;
}
if (lower == root->minValue && upper == root->maxValue) {
root->countSegment++;
return true;
}
if (!root->left) {
return false;
}
int mid = root->left->maxValue;
if (upper <= mid) {
return addSegment(lower, upper, root->left);
}
if (!root->right) {
return false;
}
if (lower > mid) {
return addSegment(lower, upper, root->right);
}
addSegment(lower, mid, root->left);
addSegment(mid+1, upper, root->right);
return true;
}
/** * get the count of segment contain the value * * @param value value for search * @param root segment tree root node * * @return return the count of segment */
int getSegmentCount(int value, TreeNode * root){
if (value < root->minValue || value > root->maxValue) {
return 0;
}
int count = root->countSegment;
if (root->maxValue == root->minValue) {
return count;
}
int mid = root->left->maxValue;
if (value <= mid) {
count += getSegmentCount(value, root->left);
}
if (value > mid) {
count += getSegmentCount(value, root->right);
}
return count;
}
int main(int argc, const char * argv[]) {
//这里的temp内容不一定是非要连续的
vector<int> temp = {0,1,2,3,4,5,6,7};
TreeNode * root = InitSegmentTree(temp, 0, (int)temp.size()-1);
add(4, root);
add(6, root);
cout<<getCount(4, 6, root)<<endl;
addSegment(2, 5, root);
addSegment(4, 6, root);
cout<<getSegmentCount(3, root)<<endl;
// insert code here...
std::cout << "Hello, World!\n";
return 0;
}
代码我测试了一些用例,暂时没有问题,尤其应用场景1是leetcode上的一个题目,用这个代码已经A掉了。
一些简单的疑问
我最开始看到线段树,以为是建一个节点,然后如二叉树一样,每次进行一个节点的插入操作。后来发现,原来线段树一开始就建立好了,后面的操作都是在改变节点的标记数据。
线段树在计数方面非常方便。