八皇后
八皇后问题
【题目要求】
求解如何在一个8*8的棋盘上无冲突地摆放8个皇后棋子。在国际象棋里,皇后的移动方式为横竖交叉的,
因此在任意一个皇后所在位置的水平、竖直,以及45°斜线上都不能出现皇后的棋子。
【题目分析】
如果一个一个的遍历运算时间会过长。
八皇后采用行(列)为单位,先去掉一个判断条件,一行(列)满足一个皇后,再进行判断一列(行)和对角线上是否有
之前定义的皇后,如果没有先将皇后定义到这,进行下一个皇后的安放,执行到8个皇后全都安放完或者执行到某行时没有安
放皇后的位置,就返回上一层,改变皇后的位置,继续往下一层执行,如果某行的位置列都执行过而下一行没有安放皇后的
位置,就继续往上一层返回(例:当执行到第5行时,先与前面的皇后位置进行判断,看皇后能放哪,选择第一个符合皇后的
位置,进行执行第6行,第6行从第1列开始判断,看能不能安放皇后,如果能则执行第7行,如果第6行都遍历过没有皇后的安
放位置,就返回第5行继续进行后面列是否有安放皇后的位置,如果有就重复上面的步骤,如果没有就返回第4行,依次遍历
所以符合某行符合前面皇后位置的所以点)。
【思想】:
回溯法:
当把问题分为若干步骤并递归求解时,如果当前步骤没有合法选择,则函数将返回一级递归调用,这就是回溯。不撞墙不回头的思想。
【易懂版】
【代码】:
【代码分析】
定义了两个函数:
int型函数用于判断某个点的列或左上或右上或右下或左下是否有皇后,有返回0,没有返回1
void型函数用于递归运算,函数接收一个int型表示行,一个n表示n皇后,一个数组表示皇后图,函数里用for循环遍历此行所有的点,看是否有符合条件的点,有就标记此点,令此点值为1,递归执行下一行,没有返回上一层递归(递归语句后面要再将定义的1置0,你假设的此点能当皇后,无论找到或找不到8个皇后,都不再执行,因为你一行有多个皇后,判断下一行时,找符合皇后就更少了,到某一行就找不到符合的点,但是一行又多了几个皇后,重复进行,直到第一行遍历完结束。
【N皇后】
前面的也可以扩展为n皇后只需将8改为n,并加上一个输入语句就行了
【思维规律版】
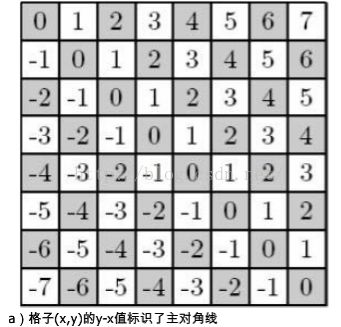
【图片分析】
对应行数x和列数y,x-y和x+y可以看出每一个对角线的值是一样的,用对角线的值来判断皇后是否可以安放,能节省很多代码且运行时间减少。
【代码1】
#include<stdio.h>
int C[10],n,count;
void print()
{
printf("answer:%d\n",count);
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
if(C[i]==j) printf("1 ");
else printf("0 ");
printf("\n");
}
//printf("\n");
}
void search(int cur)
{
if(cur==n)
{
count++;
print();
return ;
}
int i,j;
for(i=0;i<n;i++)
{
int ok=1;
C[cur]=i; // 假设第cur行第i列能放皇后,进行下面的判断,看是否假设成立
for(j=0;j<cur;j++) // j执行到cur-1,因为执行的这行与前面的皇后进行位置进行比较,不能同列或同对角线
{
if(C[cur]==C[j]||cur-j==C[cur]-C[j]||cur-j==C[j]-C[cur]) // 判断是否同列或同对角线
{
ok=0;
break;
}
}
if(ok) search(cur+1); // 如果不同列或同对角线则继续进行递归
}
}
int main()
{
scanf("%d",&n);
search(0);
printf("%d\n",count);
return 0;
}
【代码分析】
用cur表示本行,j表示之前的行,C[cur]来表示本行皇后所在的列数,C[j]表示表示之前皇后所在的列数
【代码2】
#include<stdio.h>
int vis[3][20],C[10],tot=0,n;
void print()
{
printf("answer:%d\n",tot);
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
if(C[i]==j)
printf("1 ");
else printf("0 ");
printf("\n");
}
//printf("\n\n");
}
void search(int cur)
{
int i,j;
if(cur==8)
{
tot++;
print(); // 输出八皇后的图
return ;
}
for(i=0;i<n;i++)
{
if(!vis[0][i]&&!vis[1][cur+i]&&!vis[2][cur-i+n])
// vis[1][cur+i]表示副对角线,vis[2][cur-i+n]表示主对角线
{
C[cur]=i; // 可用于输出图
vis[0][i]=vis[1][cur+i]=vis[2][cur-i+n]=1; // 表示某个位置有皇后,其他皇后不能与之同列或同对角线
search(cur+1);
vis[0][i]=vis[1][cur+i]=vis[2][cur-i+n]=0;
// 必须置0,不然当前几层for循环第一个符合要求的时,执行到某一层发现没法继续执行,
// 就要返回,但你没有置0,返回后都无法继续执行
}
}
}
int main()
{lie
scanf("%d",&n);
search(0);
printf("%d\n",tot);
return 0;
}
【代码分析】
v[3][20]数组表示数据的位置,v[0]表示列,v[1]表示副对角线,v[2]表示主对角线,二维数组的列的值表示第几列和上图对角线的值,v数组的值表示此列或此对角线有没有皇后,有置为1,没有为0。
此代码和第一个代码一样需要递归后面置0,而第二个代码中,数组储存的是每行皇后的列数,当执行完时,会被下一个列数替代,只是判断本行的行--列和行+列和列与前面皇后的行--列和行+列和列是否相等相等说明此点不能安放皇后。
看前面的对角线图会让你更能理解这些话。