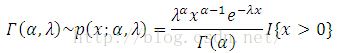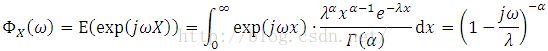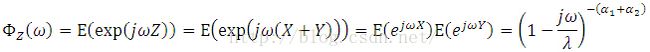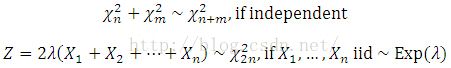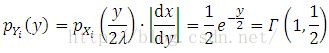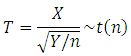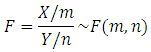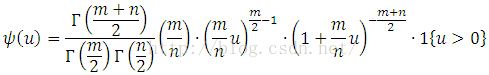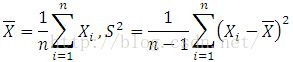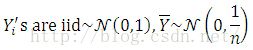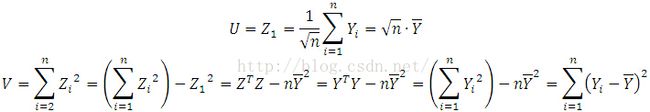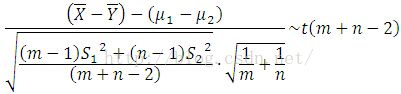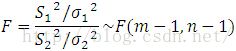Statistics Distribution Of Normal Population

STATISTICS DISTRIBUTION OF NORMAL POPULATION

Ethan

FOR MUM AND MUM'S MUM

In probability and statistics, a statistic is a function of samples. Theoretically, it is also a random variable with a probability distribution, called statistics distribution. As a statistic is a basis of inference of population distribution and characteristics, to determine a distribution of a statistic is one of the most fundamental problems in statistics. Generally speaking, it is rather complicate to determine a precise distribution of a statistic. But, for normal population, there are a few effective methods. This work will introduce some common statistics distributions of normal population and derive some important related theorems.

 

Digression

Let’s consider the probability distribution of Y = X², where X ~ N(0, 1). The probability density of Y is given by

Therefore, Y ~ Gamma(1/2, 1/2), where

By using Gamma function (See Appendix I), one can determine the expectation and variance of Y, E(Y) = alpha/lambda, Var(Y) = alpha/lambda².

The characteristic function of Gamma probability density is given by

where X ~ Gamma(alpha, lambda).

Consider the distribution of a summation, Z, of two independent random variables, X ~ Gamma(alpha1, lambda) and Y ~ Gamma(alpha2, lambda). The characteristic function of Z is given by

Thus, Z ~ Gamma(alpha1+alpha2, lambda).

 

Chi² Distribution

Suppose a population X ~ N(0, 1), X₁, …, X_n are iid, then

It is easy to check that E(Y)=n, D(Y)=2n.

Two important properties of Chi² distribution:

Proof:

The first one is trivial.

To see the second one, let Y_i = 2(lambda)X_i, then

Therefore,

This completes the proof. #

t-Distribution

Suppose X ~ N(0,1), Y ~ Chi²(n), and X and Y are independent, then

of which the probability density is given by

One can check that, when n>2, E(T)=0, D(T)=n/(n-2).

F-Distribution

Suppose X ~ Chi²(m), Y ~ Chi²(n), and X and Y are independent, then

of which the probability density is given by

Theorem 1

Suppose X₁, …, X_n are samples extracted from a normal population N(mu, sigma²), with a sample mean and a sample variance,

then, (1)(2)(3)(4)

Proof:

Formula (1) can be easily checked by performing Gaussian normalization.

For (2) and (3),

where

Now construct a finite-dimensional linear transformation A from Y to Z,

One can show that A is an orthonormal matrix. Further,

Therefore, Z_i’s are also iid ~ N(0, 1).

Consequently, U and V are independent, where

Since V ~ Chi²(n-1), then

To see (4), now that U’ and V’ are independent, satisfying

by the definition of t-distribution, we have

This completes the proof. #

Theorem 2

Suppose X₁, …, X_m and Y₁,…, Y_n are samples taken from two normal populations N(mu₁, sigma²), N(mu₂, sigma²), respectively, and they are all independent, then,

Hint: This can be shown by applying Theorem 1.

Theorem 3

Suppose X₁, …, X_m and Y₁, …, Y_n are samples taken from two normal populations N(mu₁, sigma₁²), N(mu₂, sigma₂²), respectively, and they are all independent, then,

Hint: This can be shown by using the definition of F-distribution.

APPENDIX

I. Gamma Function

Gamma function is defined as

which has following properties

Proof:

This completes the proof. #

II. Probability Density after Transformation

Suppose random vectors X, Y are in Rⁿ and a bijective operator T is defined as

If the probability density of X is p_X(x), then that of Y is given by

Proof:

The cumulative probability function of Y is given by

Hence,

This completes the proof. #

This theorem can be used to determine the probability density typical of the form “Z=X/Y”, “Z=X+Y”, etc., by introducing an irrelevant variable U and integrating the joint distribution of (Z, U)^T to get the marginal distribution of Z, as long as T is bijective.