KNN分类算法的实现
KNN分类算法的实现
摘 要 KNN算法是数据挖掘技术中比较常用的分类算法, 由于其实现的简单性, 在很多领域得到了广泛的应用。本文介绍了传统的KNN算法,并用MATLAB将其实现。
关键词 数据挖掘,分类算法,KNN分类
Implementation of K Nearest Neighbors Algorithm
ABSTRACT KNN algorithm has been widely used in many data mining areas due to its simplicity.This paper introduces the traditional KNN algorithm, using MATLAB to realize it.
KEYWORDS Data mining ,sorting Algorithm,KNN classification
1.引言
分类是数据挖掘领域中一种重要的技术, 它是从一组已知的训练样本中发现分类模型, 并且使用这个分类模型来预测待分类样本。目前比较常用的分类方法有:决策树、神经网络、KNN、SVM 和贝叶斯方法等, 其中KNN 算法以其实现的简单性及较高的分类准确性在各领域得到了广泛的应用。
2.KNN算法概述
KNN算法是一个理论上比较成熟的方法,最初由Cover和Hart于1968年提出,其思路非常简单直观,易于快速实现,以及错误低的优点。KNN 分类算法的主要思想是:先计算待分类样本与已知类别的训练样本之间的距离或相似度, 找到距离或相似度与待分类样本数据最近的K 个邻居;再根据这些邻居所属的类别来判断待分类样本数据的类别。如果待分类样本数据的K个邻居都属于一个类别, 那么待分类样本也属于这个类别。否则, 对每一个候选类别进行评分, 按照某种规则来确定待分类样本数据的类别。
3.KNN算法分析
K近邻法是由Cover 和Hart 于1968 年提出的, 是当k = 1 时的一种特定的NN (NearestNeighbor) , NN 强调最近点的重要性, 而KNN 则从整体考虑, 是一种更为普遍的方法, 理论上认为错误率比NN 低。K近邻算法的思想很简单: 给一篇待识别的文章, 系统在训练集中找到最近的k 个近邻, 看这k 个近邻中多数属于哪一类, 就把待识别的文章归为那一类。下面, 介绍k近邻法的数学模型。K近邻算法描述如下:
1) 根据特征项集合重新描述训练文本向量。
2) 在新文本到达后, 根据特征词分词新文本, 确定新文本的向量表示。
3) 在训练文本集中选出与新文本最相似的k 个文本。
4) 在新文本的k 个邻居中, 依次计算每类的权重。
5) 比较类的权重, 将文本分到权重最大的类别中。
4实验与结果分析
在MATLAN中先设定两类数据,第一类数据用以下代码实现:
mu1=[0 0]; %均值
S1=[0.3 0;0 0.35]; %协方差
data1=mvnrnd(mu1,S1,100); %产生高斯分布数据
plot(data1(:,1),data1(:,2),'+');
label1=ones(100,1);
hold on;
第二类数据用一下代码实现:
mu2=[1.25 1.25];
S2=[0.3 0;0 0.35];
data2=mvnrnd(mu2,S2,100);
plot(data2(:,1),data2(:,2),'ro');
label2=label1+1;
data=[data1;data2];
label=[label1;label2];
设定待测试数据:
for ii=-3:0.1:3
for jj=-3:0.1:3
test_data=[ii jj]; %测试数据
label=[label1;label2];
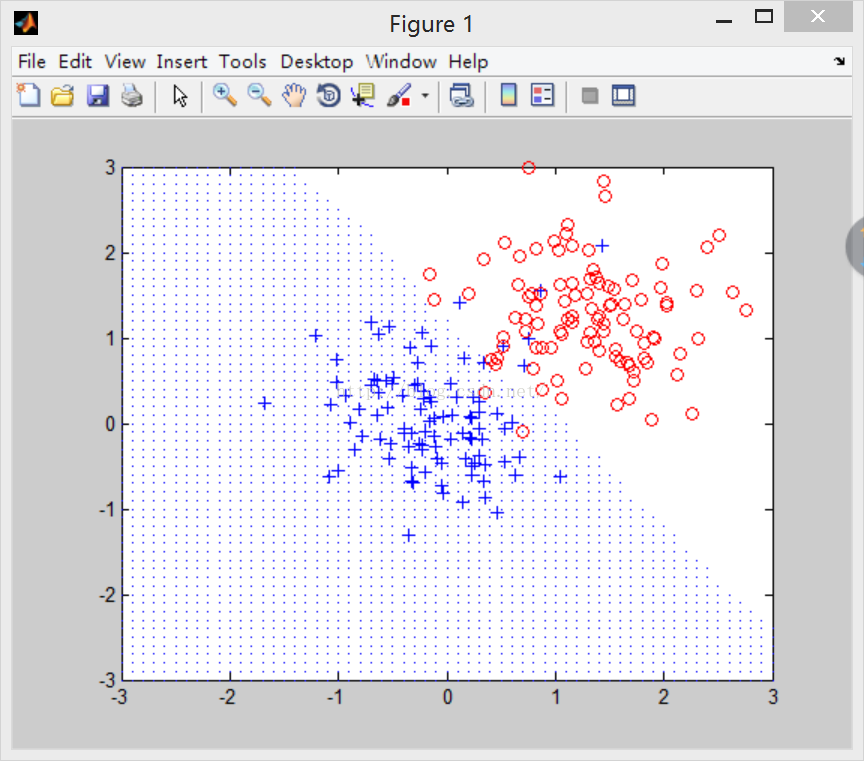
使用KNN算法,设定k=11,结果如下图:
图1 KNN算法实现结果1
设定K=3,结果如下图:
图2 KNN算法实现结果2
设定K=30,实验结果如下图:
图3 KNN算法实现结果3
5结语
KNN算法简单直观,易于实现,通过以上实验在MATLAB平台下实现了KNN算法,也可以看出K值得选取对KNN算法影响很大。
参考文献
[1] 潘丽芳,杨炳儒.基于簇的K最近邻(KNN)分类算法研究.计算机工程与设计,2009,30(18):4260-4262.
[2] 张著英,黄玉龙,王翰虎.一个高效的KNN分类算法.计算机科学,2008,35(3):170-172.
[3] 张运良,张全.柔性KNN算法研究[J].计算机工程与应用,2007,43(34):25-28.
[4]陈安, 陈宁, 周龙骧, 等.数据挖掘技术及应用.北京:科学出版社,2006
附录
源代码:
clear all;
close all;
clc;
%%第一个类数据和标号
mu1=[0 0]; %均值
S1=[0.3 0;0 0.35]; %协方差
data1=mvnrnd(mu1,S1,100); %产生高斯分布数据
plot(data1(:,1),data1(:,2),'+');
label1=ones(100,1);
hold on;
%%第二个类数据和标号
mu2=[1.25 1.25];
S2=[0.3 0;0 0.35];
data2=mvnrnd(mu2,S2,100);
plot(data2(:,1),data2(:,2),'ro');
label2=label1+1;
data=[data1;data2];
label=[label1;label2];
K=11; %两个类,K取奇数才能够区分测试数据属于那个类
%测试数据,KNN算法看这个数属于哪个类
for ii=-3:0.1:3
for jj=-3:0.1:3
test_data=[ii jj]; %测试数据
label=[label1;label2];
%%下面开始KNN算法,显然这里是11NN。
%求测试数据和类中每个数据的距离,欧式距离(或马氏距离)
distance=zeros(200,1);
for i=1:200
distance(i)=sqrt((test_data(1)-data(i,1)).^2+(test_data(2)-data(i,2)).^2);
end
%选择排序法,只找出最小的前K个数据,对数据和标号都进行排序
for i=1:K
ma=distance(i);
for j=i+1:200
if distance(j)<ma
ma=distance(j);
label_ma=label(j);
tmp=j;
end
end
distance(tmp)=distance(i); %排数据
distance(i)=ma;
label(tmp)=label(i); %排标号,主要使用标号
label(i)=label_ma;
end
cls1=0; %统计类1中距离测试数据最近的个数
for i=1:K
if label(i)==1
cls1=cls1+1;
end
end
cls2=K-cls1; %类2中距离测试数据最近的个数
if cls1>cls2
plot(ii,jj); %属于类1的数据画小黑点
end
end
End