【数据结构与算法】链表问题集锦

参考自：http://wuchong.me/blog/2014/03/25/interview-link-questions/（Jark's Blog）

链表问题在面试过程中也是很重要也很基础的一部分，链表本身很灵活，很考查编程功底，所以是很值得考的地方。

节点定义如下：

struct Node{
    int val;
    struct Node* next;
};

1、以O(1)时间删除某个节点

题目描述：给定链表的头指针和一个节点指针，在O(1)时间删除该节点。[Google面试题]

分析：这种题目一般的做法是「狸猫换太子」，也即把下一个节点的值赋给需要删除的节点，然后删除下一个节点。

//O(1)时间删除链表节点，从无头单链表中删除节点
void DelNode(struct Node* node)
{
        assert(node != NULL);
        assert(node -> next != NULL);
        node -> val = node -> next -> val;
        node -> next = node -> next -> next;
        delete node -> next;
}

需要注意的是该办法并不适用于删除尾节点。
参见 leetcode #237. Delete Node in a Linked List

2、单链表的反转

题目描述：输入一个单向链表，输出逆序反转后的链表。

分析：单链表的反转通常有两种，一种是使用三个临时指针 pre、cur、next 在链表上循环一遍即可，这是一种非递归的方法，另一种是使用递归的方法，要求思路清晰。

//非递归
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode *pre, *cur, *next;
        if(head == NULL || head -> next == NULL)                //处理链表为空或链表只有一个节点的情况
            return head;
        pre = NULL;
        cur = head;
        next = head -> next;
        while(next != NULL)                                     //next 为空是结束标志，其实就是 cur 从头遍历到尾！
        {
            cur -> next = pre;
            pre = cur;
            cur = next;
            next = next -> next;
        }
        cur -> next = pre;
        return cur;       
    }
};

//递归
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(head == NULL || head -> next == NULL)          //第一个条件是判断异常，第二个条件是结束判断
            return head;
        
        ListNode *newHead = reverseList(head -> next);    //先递归，再处理
        head -> next -> next = head;                      //在当前节点处理下一节点，让下一节点指向当前节点并将当前节点指向NULL
        head -> next = NULL;                              //NULL的设置源于头节点最后指向NULL，对中间节点无实际影响
        
        return newHead;                                   //返回新的头指针
    }
};

leetcode传送门：  206. Reverse Linked List

3、删除单链表倒数第k个节点

题目描述：输入一个单向链表，输出该链表中倒数第k个节点。

分析：设置两个指针 p1、p2，首先 p1 和 p2 都指向 head，然后 p2 向前走 k - 1步，然后 p1 和 p2 同时向前移动，直至 p2 走到链表末尾，此时 p1 就指向倒数第 k 个节点。

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        if(head == NULL || n <= 0)                  //排除特殊情况
            return head;
            
        ListNode *p1 = head, *p2 = head;
        
        if(n == 1)                                  //「狸猫换太子」不适用于删除最后节点
        {
            if(p1 -> next == NULL)
                return NULL;
            while(p1 -> next -> next != NULL)
                p1 = p1 -> next;
            p1 -> next = NULL;
            return head;
        }
        
        int i = n - 1;
        while(i)                     //用 i 来判断给的 n 是否大于链表长度，考虑到删除倒数第n+1个(链表长n)，此处不能用 while(i--)
        {
            if(p2 -> next)
            {
                p2 = p2 -> next;
                --i;                              
            }
            else
                break;
        }
        if(i)
            return head;
        
        while(p2 -> next != NULL)
        {
            p2 = p2 -> next;
            p1 = p1 -> next;
        }
        
        p1 -> val = p1 -> next -> val;
        p1 -> next = p1 -> next -> next;
        
        return head;
        
    }
};

参见 leetcode #19 Remove Nth Node From End of List

4、求链表中间的节点

题目描述：求链表的中间节点，如果链表的长度为偶数，返回中间两个节点的任意一个，若为奇数，则返回中间节点。

分析：此题的解决思路和第3题「求链表的倒数第 k 个节点」很相似。通过两个指针来完成。用两个指针从链表头节点开始，一个指针每次向后移动两步，一个每次移动一步，直到快指针移到到尾节点，那么慢指针即是所求。

代码如下：

//求链表的中间节点，对于长度为偶的链表，返回中间节点中的第一个
Node* theMiddleNode(Node *head)
{
    if(head == NULL)
        return NULL;
    Node *slow,*fast;
    slow = fast = head;

    while(fast != NULL && fast->next != NULL)
    {
        fast = fast->next->next;
        slow = slow->next;
    }
    return slow;
}

5、判断单链表是否存在环，并找到环入口节点

题目描述：输入一个单向链表，判断链表是否有环。如果链表存在环，如何找到环的入口点？

分析：通过两个指针，分别从链表的头节点出发，一个每次向后移动一步，另一个移动两步，两个指针移动速度不一样，如果存在环，那么两个指针一定会在环里相遇。按照 p2 每次两步，p1 每次一步的方式走，发现 p2 和 p1 重合，确定了单向链表有环路了。接下来，让p2回到链表的头部，重新走，每次步长不是走2了，而是走1，那么当 p1 和 p2 再次相遇的时候，就是环路的入口了。

原因目前还没搞清楚。。先记住吧。

leetcode #141. Linked List Cycle

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *p1, *p2;
        p1 = p2 = head;
        while(p2 != NULL && p2 -> next != NULL)
        {
            p2 = p2 -> next -> next;
            p1 = p1 -> next;
            if(p1 == p2)
                return true;
        }
        
        return false;
    }
};

leetcode #142. Linked List Cycle II

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        bool flag = false;
        ListNode *p1, *p2;
        p1 = p2 = head;
        
        while(p2 != NULL && p2 -> next != NULL)
        {
            p2 = p2 -> next -> next;
            p1 = p1 -> next;
            if(p2 == p1)
            {
                flag = true;
                break;
            }
        }
        
        if(flag)
        {
            p2 = head;
            while(p2 != p1)
            {
                p1 = p1 -> next;
                p2 = p2 -> next;
            }
            return p1;
        }
        else
            return NULL;
    }
};

6、判断两个链表是否相交

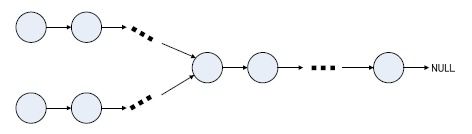
题目描述：给出两个单向链表的头指针（如下图所示），

比如h1、h2，判断这两个链表是否相交。这里为了简化问题，我们假设两个链表均不带环。

解题思路：


1、直接循环判断第一个链表的每个节点是否在第二个链表中。但，这种方法的时间复杂度为O(Length(h1) * Length(h2))。显然，我们得找到一种更为有效的方法，至少不能是O（N^2）的复杂度。

2、针对第一个链表直接构造hash表，然后查询hash表，判断第二个链表的每个节点是否在hash表出现，如果所有的第二个链表的节点都能在hash表中找到，即说明第二个链表与第一个链表有相同的节点。时间复杂度为为线性：O(Length(h1) + Length(h2))，同时为了存储第一个链表的所有节点，空间复杂度为O(Length(h1))。是否还有更好的方法呢，既能够以线性时间复杂度解决问题，又能减少存储空间？

3、转换为环的问题。把第二个链表接在第一个链表后面，如果得到的链表有环，则说明两个链表相交。如何判断有环的问题上面已经讨论过了，但这里有更简单的方法。因为如果有环，则第二个链表的表头一定也在环上，即第二个链表会构成一个循环链表，我们只需要遍历第二个链表，看是否会回到起始点就可以判断出来。这个方法时间复杂度为线性O(N)，空间复杂度为O(1)。

4、进一步考虑“如果两个没有环的链表相交于某一节点，那么在这个节点之后的所有节点都是两个链表共有的”这个特点，我们可以知道，如果它们相交，则最后一个节点一定是共有的。而我们很容易能得到链表的最后一个节点，所以这成了我们简化解法的一个主要突破口。那么，我们只要判断两个链表的尾指针是否相等。相等，则链表相交；否则，链表不相交。
所以，先遍历第一个链表，记住最后一个节点。然后遍历第二个链表，到最后一个节点时和第一个链表的最后一个节点做比较，如果相同，则相交，否则，不相交。这样我们就得到了一个时间复杂度，它为O((Length(h1) + Length(h2))，而且只用了一个额外的指针来存储最后一个节点。这个方法时间复杂度为线性O(N)，空间复杂度为O(1)。

7、扩展：链表有环，如何判断相交

题目描述：上面的问题都是针对链表无环的，那么如果链表是有环的呢?上面的方法还同样有效么?

分析：如果有环且两个链表相交，则两个链表都有共同一个环，即环上的任意一个节点都存在于两个链表上。因此，就可以判断一链表上俩指针相遇的那个节点，在不在另一条链表上。

8、扩展：两链表相交的第一个公共节点

题目描述：如果两个无环单链表相交，怎么求出他们相交的第一个节点呢？

分析：采用对齐的思想。计算两个链表的长度 L1 , L2，分别用两个指针 p1 , p2 指向两个链表的头，然后将较长链表的 p1（假设为 p1）向后移动L2 - L1个节点，然后再同时向后移动p1 , p2，直到 p1 = p2。相遇的点就是相交的第一个节点。

或者将链表2的头接在链表1后，产生一个环后将问题转换成了求环的入口，参见上面已有的答案即可。

9、总结

可以发现，在链表的问题中，通过两个的指针来提高效率是很值得考虑的一个解决方案，所以一定要记住这种解题思路。记住几种

典型的链表问题解决方案，很多类似的题目都可以转换到熟悉的问题再解决。