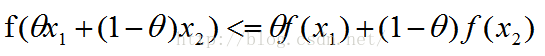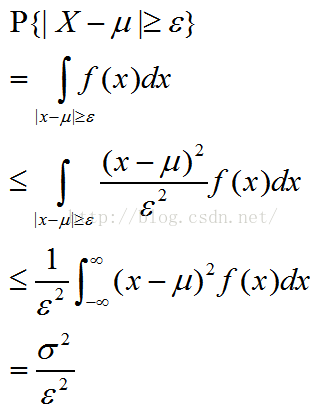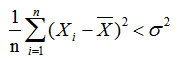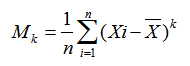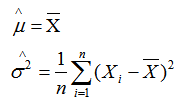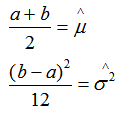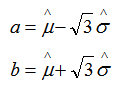2.数理统计与参数估计

注：以下内容整理于七月算法2016年4月班培训讲义，详见： http://www.julyedu.com/

内容简介：

A.重要统计量
B.重要定理与不等式
C.参数估计


A.重要统计量
一、概率与统计
概率：已知总体的分布情况，计算事件的概率
统计：总体分布未知，通过样本值估计总体的分布

二、概率统计与机器学习的关系
1.统计估计的是分布，机器学习训练出来的是模型，模型可能包含了多个分布。
2.训练与预测过程的一个核心评价指标是模型的误差。
3.误差可以是概率的形式，与概率紧密相关。
4.误差的定义方式不同，由此损失函数的定义方式也不同。

三、期望：加权平均值
离散型定义：

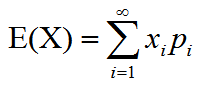
连续性定义：
 

期望的性质
1.E(C)=C
2.E(CX)=CE(X)
3.E(X+Y)=E(X)+E(Y)
证明:
 
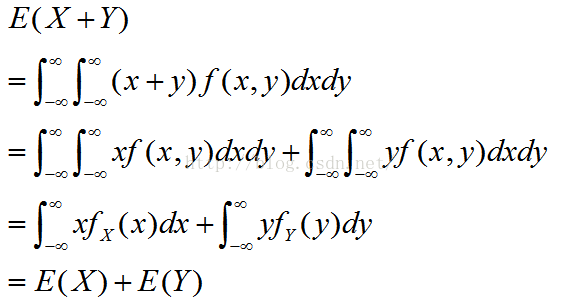
4.如果X和Y独立，则E(XY)=E(X)E(Y)
证明：
 

四、方差：相对于期望的偏离程度
 

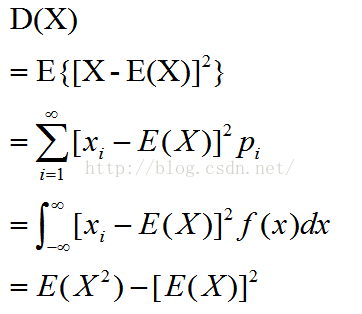
方差性质：
1.D(c)=0
2.D(X+c)=D(X)
3.D(kX)=k^2*D(X)
4.D(X+Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)}
如果X和Y独立，则D(X+Y)=D(X)+D(Y)
证明如下：


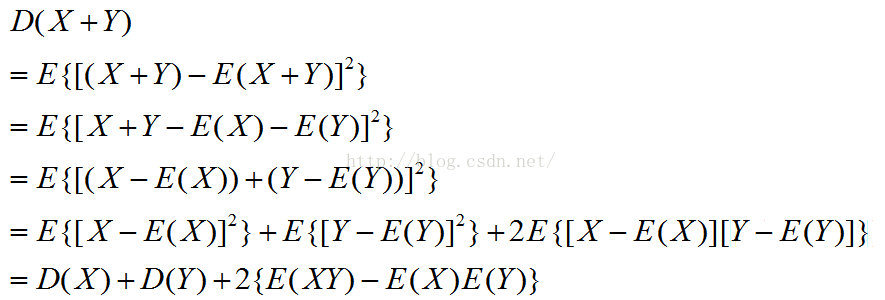
五、协方差(可用来降维)：
定义：Cov(X,Y)=E{[X-E(X)][Y-E(Y)}=E(XY)-E(X)E(Y)
协方差性质：
Cov(X,Y)=Cov(Y,X)
Cov(aX+b,cY+d)=acCov(X,Y)
Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)

六、独立、互斥、不相关
独立定义：P(XY)=P(X)P(Y)
互斥定义：P(XY)=0
不相关定义：Cov(X,Y)=0

X和Y独立
=>E(XY)=E(X)E(Y)
=>Cov(X,Y)=0
=>X和Y不相关
故X和Y独立可推出二者不相关，反之不成立。
不相关本质上指线性独立，即X和Y之间没有线性关系，但二者可能存在其他关系，所以不能保证X和Y独立。
但是，特别的，对于二维正态随机变量，X和Y不相关等价于X和Y独立。

七、协方差矩阵：
设n个随机变量(X1,X2,....Xn)，Cij=Cov(Xi,Xj)都存在，则称矩阵
 
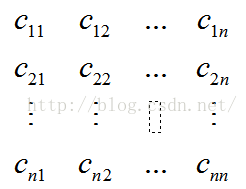
为协方差矩阵。由于Cij=Cji，所以上述矩阵为对阵矩阵。

八、协方差的上界
 
当且仅当X、Y有线性关系时，等号成立。

九、相关系数：
 
十、矩
对于随机变量X，X的k阶原点矩为：

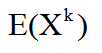
X的k阶中心距为：
 

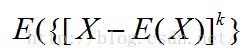
注：期望为一阶原点矩，方差为二阶中心距

B.重要定理与不等式
一.Jensen不等式
如果f是凸函数，那么：

该不等式称为Jensen不等式。
注：该不等式有扩展形式，此处略。

二.切比雪夫不等式：未知随机变量分布，只知道E(X)和D(X)，估计P{|X-E(X)|<ε}的界限
设随机变量X的的期望为μ，方差为α^2，对于任意的正数ε,有：

该不等式称为切比雪夫不等式。

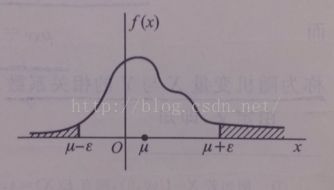
图形化描述：

证明如下：

切比雪夫不等式的意义：说明随机变量X的方差越小，事件P{|X-E(X)|<ε}发生的概率越大，即X的取值越集中在期望E(X)附近分布。

三.大数定理

1.辛钦大数定律

2.伯努利大数定理

大数定理的意义：当n很大时，随机变量X1,X2...Xn的平均值Yn在概率意义下无限接近于期望μ。
或者，可以说当n很大时，频率收敛于概率。

四.中心极限定理

C.参数估计
一.样本统计量

计算样本方差的时候为什么不是除以n而是n-1呢？
为了得到无偏估计。
那为什么除以n就是“有偏估计”呢？
以下证明旨在说明为什么除以n有误差，并不能说明为什么要除以n-1而不是n-2或n-3...
假设随机变量X的期望μ已知，而方差α^2未知。根据方差的定义，有

由此可得：

上式是基于期望μ已知的情况下计算的结果，现在考虑μ未知的情况。
我们使用样本均值代替μ，有

所以，除非样本均值恰好等于随机变量X的期望μ，否则我们一定有

这就说明了除以n是有误差的，但是，依然没有说明为啥要除以n-1。

二.样本的矩
1.k阶样本原点矩

2.k阶样本中心矩

三.矩估计
基于样本矩依概率收敛于相应的总体矩，样本矩的连续函数依概率收敛于相应的总体矩的连续函数，
我们使用样本矩作为相应的总体矩的估计量，而以样本矩的连续函数作为相应的总体矩的连续函数
的估计量，这种估计方法为矩估计法。

例1：在正态分布的总体中采样得到n个样本：X1,X2...Xn,试求μ和α^2的矩估计量。

例2：设总体X在[a,b]上服从均匀分布，a和b未知， X1,X2...Xn是来自X的样本，试求a,b的矩估计量。
由矩估计可得：

我们令总体均值、总体方差分别等于矩估计的样本均值、样本方差

解得：

四.极大似然估计(已经发生的，就是概率最大的!)
1.直观解释：设某分布的参数为θ，X1,X2...Xn为来自该分布的样本，即X1,X2...Xn已经发生了，
我们要估计的θ满足这样一个条件：在该分布下，使得X1,X2...Xn同时发生的概率最大。
举个例子：箱子里有5个球，白球和黑球，已知两种颜色球的数量比是4:1，但是不知道白球是4还是黑球是4。
即不确定黑:白=4:1 OR 白:黑=4:1，现在要对此进行估计。
现在有放回的从箱子中取球，取了3次，每次都是黑球，我们记为事件A,那么，
如果 黑:白=4:1，则P(A)=0.8*0.8*0.8=0.512
如果 白:黑=4:1，则P(A)=0.2*0.2*0.2=0.008
所以，基于事件A已经发生了这个事实，我们有51.2%的把握相信黑:白=4:1，而只有0.8%的把握相信白:黑=4:1。
因此，一般的讲，我们估计结果为黑:白=4:1。
2.似然函数

例1： 设X~b(1,p)，X1,X2,...,Xn是来自X的一个样本，试求参数p的极大似然估计量。
设x1,x2,...,xn是相应于样本X1,X2,...,Xn的样本值。X的分布律为：

故似然函数为：