机器学习笔记05:正则化(Regularization)、过拟合(Overfitting)
(一)过拟合问题(The Problem of Overfitting)
不管是在线性回归还是在逻辑回归中,我们都会遇到过拟合的问题。先从例子来看看什么是过拟合。
i.线性回归中的过拟合
还是以房价预测为例,来看几张张图片:
1.欠拟合(Underfitting)

上图中,我们用一条直线 hθ(x)=θ0+θ1x 来拟合训练集中数据,但是明显何以看出的是,房价不会随面积成比例地增长,这种情况,称之为 欠拟合。
2.过拟合(Overfitting)

如上图所示,我们用一条高次的曲线 hθ(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4 来拟合训练集中的数据,因为参数过多,对训练集的匹配度太高、太准确,以至于在后面的预测过程中可能会导致预测值非常偏离合适的值,预测非常不准确,这就是 过拟合。
3.合适的拟合(Properfitting)
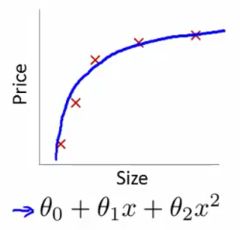
如上图,如果选用一条合适的曲线,比如说抛物线 hθ(x)=θ0+θ1x+θ2x2 来拟合上面的训练集就非常的合适。这就是一个比较恰当的 假设函数(hypothesis function)。
所以,总结一下,一般在实际应用中不会遇到欠拟合的情况。而过拟合却会经常出现。一盘情况下,过拟合(Overfitting)就是:如果我们使用了太多的特征(features)来训练一个假设函数,就会使其对训练集的匹配度非常高(误差几乎为零: J(θ)=12m∑mi=1(θTx(i)−y(i))2 ),但是不能推广到其他未知数据上,也就是对于训练集之外的输入,不能做出正确的预测。
ii.逻辑回归中的过拟合
再来看看逻辑回归中的过拟合问题,以肿瘤预测为例。
1.欠拟合(Underfitting)
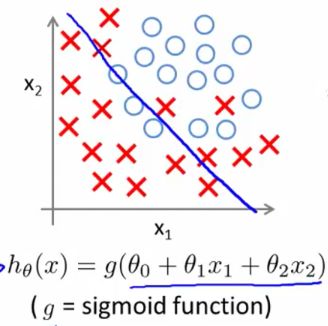
上图中是在逻辑回归的样本中,用一条直线 z=θ0+θ1x+θ2x 来拟合训练集,明显效果不够理想。这种情况是 欠拟合。
2.过拟合(Overfitting)
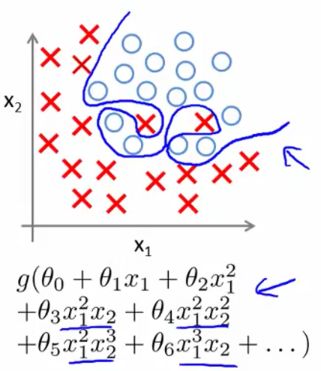
而这张图,用了一个高次假设函数来拟合,使得每个样本都严格地分局于 决策边界(decision boundary)的两侧,这种情况叫做 过拟合。
(PS:上面提到的决策边界以及函数g,请参考上一篇:《机器学习笔记04:逻辑回归(Logistic regression)、分类(Classification)》
3.合适的拟合(Properfitting)

而上面这个二次假设函数则比较合适的拟合了训练集中的数据。
iii.处理过拟合(Addressing overfitting)
面对过拟合问题,我们可以像在线性回归中 Debug 误差函数(hypothesis function)那样来画图纠错。以房价预测为例,假设有样本选取了太多的特征:
| features | representation |
|---|---|
| x1 | size of house |
| x2 | no. of bedrooms |
| x3 | no. of floors |
| x4 | age of house |
| x5 | average income in neighborhood |
| x6 | kitchen size |
| … | … |
| x100 | traffic situation |
然后我们训练出来了一个假设函数 hθ(x) 假若发现我们训练得到的假设函数对于新的输入,其预测非常的不好。我们可以将其图像画出来,如果像下图中那样过于匹配训练集中的数据,可能就是过拟合了。其原因大多是因选取了太多的特征(features)。

通常,有两种主要的办法来处理过拟合为题:
1.减少特征的数量
减少特征数量又包括 人工手动减少特征数量 和 使用模型选择算法,后者会在后面的文章中讲到。
2.正则化
正则化(Regularization)则不会减少特征的数量,因为我们可能真的需要很多特征,但是此方法会使某个特征 θj 的值减小,而且当特征数量很多时,正则化也能工作得很好。后面会具体阐述。
(二)误差函数(Cost Function)
现在我们就来讲一讲正则化(Regularization)。首先,看一下之前的两张图片:

上面的左图是一个恰当的拟合,其假设函数是一个二次函数(quadratic function);而右图是过拟合的情况,其假设函数是一个四次函数(quartic function)。那怎么能够在不删除特征(不减少特征)的情况下,处理过拟合情况呢。方法如下:
假设我们的假设函数为 hθ(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4 。与左图相比,因为三次项和四次项导致了过拟合的现象,所以们可以惩罚三次项和四次项,具体方法是在误差函数中加入惩罚项:
因为我们要最小化 误差函数,所以在梯度下降开始到完成的过程中式子 α∂∂θjJ(θ) 会从某一个值趋近于0( 为何会收敛于0,我暂时不理解,不能证明),完成时,就会有 θ3≈0 和 θ4≈0 。这就使得之前的 假设函数:
以惩罚(penalize)三次项为例说说我个人的见解,对 θ3 求偏导数:
但是,通常情况下,我们可能无法提前知道到底是哪个参数(特征),或哪个项引起了过拟合。所以一般将除去 θ0 之外的其他参数都正则化(因 θ0 不是任何特征的参数,无必要正则化):
但是,当 λ 过大时,会使得 θ1≈θ2≈...≈θn≈0 ,使得假设函数 hθ(x)≈θ0 :
 所以
λ 过大也会产生欠拟合的现象。
所以
λ 过大也会产生欠拟合的现象。
三、正则化的线性回归(Regularized Linear Regression)
i.梯度下降(Gradient Descent)
正则化的梯度下降形式为:
ii.Normal Equation
正则化的Normal Equation的形式为:
四、正则化的逻辑回归(Regularized Logistic Regression)
之前我们讲到过过拟合的现象:

假设函数为:
如有错误,期望您能纠正,留言或者是e-mail:[email protected]
——– 转载请注明出处——–