算法总结:最短路
最短路
一、引入
给定两点之间有多条路径,且长度不一定都相等,让你求其最短的那条路径即为最短路问题。
解决最短路问题的算法有以下三种:
1. Dijkstra;
2. SPFA;
3. Floyd;
二、算法介绍
1、Dijkstra
u 从一个点出发,到达其他顶点的最短路径的长度。
u 基本操作:松弛
u d[u]+map[u, v]< d[v]这样的边(u,v)称为紧的(tense),可以对它进行松弛(relax): d[v] = d[u]+w
u 最开始给每一个点一个很大的d值,从d[s]=0开始,不断的对可以松弛的点进行松弛,不能松弛的时候已经求出了最短路了
2、SPFA
SPFA(Shortest Path Faster Algorithm)(队列优化)算法是求单源最短路径的一种算法,在Bellman-ford算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。
设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,而且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
3、Floyd
用一个数组记录每一对顶点的距离,然后遍历每一个点,让其做中点,判断是否可以通过这个点让某对顶点的距离更小,如果可以则更新该对顶点的距离。
三、算法实现
1、Dijkstra
² Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止
² 注意该算法要求图中不存在负权边。
² 可以证明,具有最小的d[i](临时最短路)值的(还没加入最短路)点在此以后无法松弛
² 所以每次找最近的点进行松弛操作
1、在开始之前,认为所有的点都没有进行过计算,dis[]全部赋值为极大值(dis[]表示各点当前到源点的最短距离)
2、源点的dis值明显为0
3、还没算出最短路的点中dis[]最小的一个点u,其最短路就是当前的dis[u]
4、松弛操作:对于与u相连的所有点v,若dis[u]+cost[u][v]比当前的dis[v]小,更新dis[v]。
5、重复3,4直到源点到所有点的最短路都已求出
代码实现:
void dijkstra(int a)
{
int i,vis[105];
for(i=1;i<=n;i++)//初始化dis[],vis[]
{
dis[i]=max;
vis[i]=0;
}
dis[a]=0;
while(1)
{
int v=-1;
for(i=1;i<=n;i++)
if(!vis[i]&&(v==-1||dis[i]<dis[v]))
v=i;
if(v==-1)//所有路径均已标记完毕
break;
vis[v]=1;//标记
for(i=1;i<=n;i++)
dis[i]=min(dis[i],dis[v]+cost[v][i]);//更新dis[]
}
}
2、SPFA
SPFA 在形式上和宽度优先搜索非常类似,不同的是宽度优先搜索中一个点出了队列就不可能重新进入队列,但是SPFA中一个点可能在出队列之后再次被放入队列,也就是一个点改进过其它的点之后,过了一段时间可能本身被改进,于是再次用来改进其它的点,这样反复迭代下去。
代码实现:
void spfa(int sx)
{
queue<int>q;
memset(dis,INF,sizeof(dis));
memset(vis,0,sizeof(vis));
q.push(sx);
dis[sx]=0;
vis[sx]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=A[i].next)
{
int v=A[i].to;
if(dis[v]>dis[u]+A[i].val)
{
dis[v]=dis[u]+A[i].val;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
}
3、Floyd
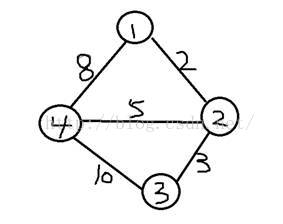
假设有这么一个图:
包含顶点1,2,3,4以及两个点的距离,
for( k=1; k<=n ; k++ ) 这个k就是从第一个顶点到最后一个顶点依次
当做中间节点,然后i从第一个点到最后一个点的遍历,更新到j
的距离,如果i从k点到j点的距离小于i直接到j点的距离,那
么就把i到j的距离更新为,i从k到j的距离。上边代码的dist就
存放i到j的最短距离。
例如上边的图中:
当2为中间节点的时候,1直接到4的距离是8,但是1从2到4
的距离是7,所以当2为中间节点的时候dis[1][4]就等于7,同理3
到4的距离是8。
这就是floyd三层for循环的意思和作用,每个点当做中间节点依次
更新为路径更短的值,最后就把任意两点的最短距离得到。
初始化为:
for( i=1;i<=n;i++ )
for(j=1; j<=n; j++)
{
If(i==j) dist[i][j] = 0;
else dist[i][j] = inf;
}
核心代码实现:
void Floyd()
{
int i,j,k;
for( k=1 ; k<=n ; k++ )
for( i=1 ; i<=n ; i++ )
for( j=1 ; j<=n ; j++ )
if( dist[i][k] + dist[k][j] < dist[i][j] )
dist[i][j] = dist[i][k] + dist[k][j];
}
四、例题解析
例一:HDU 1874畅通工程续
Problem Description
某省自从实行了很多年的畅通工程计划后,终于修建了很多路。不过路多了也不好,每次要从一个城镇到另一个城镇时,都有许多种道路方案可以选择,而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。
现在,已知起点和终点,请你计算出要从起点到终点,最短需要行走多少距离。
Input
本题目包含多组数据,请处理到文件结束。
每组数据第一行包含两个正整数N和M(0<N<200,0<M<1000),分别代表现有城镇的数目和已修建的道路的数目。城镇分别以0~N-1编号。
接下来是M行道路信息。每一行有三个整数A,B,X(0<=A,B<N,A!=B,0<X<10000),表示城镇A和城镇B之间有一条长度为X的双向道路。
再接下一行有两个整数S,T(0<=S,T<N),分别代表起点和终点。
Output
对于每组数据,请在一行里输出最短需要行走的距离。如果不存在从S到T的路线,就输出-1.
Sample Input
3 3
0 1 1
0 2 3
1 2 1
0 2
3 1
0 1 1
1 2
Sample Output
2
-1
题目大意:某省修建了很多路。不过每次要从一个城镇到另一个城镇时,都有许多种道路方案可以选择,而某些方案要比另一些方案行走的距离要短很多。现在,已知起点和终点,请你计算出要从起点到终点,最短需要行走多少距离。
参考代码:
1、 Dijkstra:
#include<cstdio>
#include<cstring>
#define max 0x3f3f3f3f
#define min(a,b) (a>b?b:a)
int dis[205],cost[205][205],n;
void dijkstra(int a)//模板
{
int vis[205];
for(int i=0;i<n;i++)
{
dis[i]=max;
vis[i]=0;
}
dis[a]=0;
while(1)
{
int v=-1;
for(int i=0;i<n;i++)
if(!vis[i]&&(v==-1||dis[i]<dis[v]))
v=i;
if(v==-1)
break;
vis[v]=1;
for(int i=0;i<n;i++)
dis[i]=min(dis[i],dis[v]+cost[v][i]);
}
}
int main()
{
int m,a,b,i,j,c;
while(~scanf("%d%d",&n,&m))
{
for(i=0;i<n;i++)//初始化
for(j=i;j<n;j++)
cost[i][j]=cost[j][i]=max;
while(m--)
{
scanf("%d%d%d",&a,&b,&c);
cost[a][b]=cost[b][a]=min(cost[a][b],c);//可能有重边
}
scanf("%d%d",&a,&b);
dijkstra(a);
if(dis[b]==max)
printf("-1\n");
else
printf("%d\n",dis[b]);
}
return 0;
}
2、SPFA:
#include<queue>
#include<cstring>
#define INF 0x3f3f3f3f
using namespace std;
int dis[205],vis[205],head[1005],num,k;
struct node//定义结构体
{
int from,to,val,next;
}A[1005];
void chan(int a,int b,int c)//给相连通的两个城镇赋值
{
node e={a,b,c,head[a]};
A[num]=e;
head[a]=num++;
}
void spfa(int sx)//模板
{
queue<int>q;
memset(dis,INF,sizeof(dis));
memset(vis,0,sizeof(vis));
q.push(sx);
vis[sx]=1;
dis[sx]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=A[i].next)
{
int v=A[i].to;
if(dis[v]>dis[u]+A[i].val)
{
dis[v]=dis[u]+A[i].val;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
if(dis[k]==INF)
printf("-1\n");
else
printf("%d\n",dis[k]);
}
int main()
{
int n,m,a,b,f,c;
while(~scanf("%d%d",&n,&m))
{
num=0;
memset(head,-1,sizeof(head));//初始化
while(m--)
{
scanf("%d%d%d",&a,&b,&c);
chan(a,b,c);
chan(b,a,c);
}
scanf("%d%d",&f,&k);
spfa(f);
}
return 0;
}
3、 Floyd:
#include<cstdio>
#define INF 0x3f3f3f3f
int s[205][205],n;
void floyd()//模板
{
int k,i,j;
for(k=0;k<n;k++)
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(s[i][k]+s[k][j]<s[i][j])
s[i][j]=s[i][k]+s[k][j];
}
int main()
{
int m,i,j,a,b,c,d,t;
while(~scanf("%d%d",&n,&m))
{
for(i=0;i<=n;i++)//初始化
for(j=0;j<=n;j++)
s[i][j]=INF;
while(m--)
{
scanf("%d%d%d",&a,&b,&c);
if(c<s[a][b])//防重边
s[a][b]=s[b][a]=c;
}
scanf("%d%d",&d,&t);
if(d==t)
{
printf("0\n");
continue;
}
floyd();
if(s[d][t]<INF)
printf("%d\n",s[d][t]);
else
printf("-1\n");
}
return 0;
}
例二:HDU- 1869六度分离
Problem Description
1967年,美国著名的社会学家斯坦利·米尔格兰姆提出了一个名为“小世界现象(small world phenomenon)”的著名假说,大意是说,任何2个素不相识的人中间最多只隔着6个人,即只用6个人就可以将他们联系在一起,因此他的理论也被称为“六度分离”理论(six degrees of separation)。虽然米尔格兰姆的理论屡屡应验,一直也有很多社会学家对其兴趣浓厚,但是在30多年的时间里,它从来就没有得到过严谨的证明,只是一种带有传奇色彩的假说而已。
Lele对这个理论相当有兴趣,于是,他在HDU里对N个人展开了调查。他已经得到了他们之间的相识关系,现在就请你帮他验证一下“六度分离”是否成立吧。
Input
本题目包含多组测试,请处理到文件结束。
对于每组测试,第一行包含两个整数N,M(0<N<100,0<M<200),分别代表HDU里的人数(这些人分别编成0~N-1号),以及他们之间的关系。
接下来有M行,每行两个整数A,B(0<=A,B<N)表示HDU里编号为A和编号B的人互相认识。
除了这M组关系,其他任意两人之间均不相识。
Output
对于每组测试,如果数据符合“六度分离”理论就在一行里输出"Yes",否则输出"No"。
Sample Input
8 7
0 1
1 2
2 3
3 4
4 5
5 6
6 7
8 8
0 1
1 2
2 3
3 4
4 5
5 6
6 7
7 0
Sample Output
Yes
Yes
题目大意:你帮忙验证一下“六度分离”是否成立,即任何2个素不相识的人中间最多只隔着6个人,即只用6个人就可以将他们联系在一起。
参考代码:
1、 Dijkstra:
#include<cstdio>
#define max 0x3f3f3f3f
#define min(a,b) (a>b?b:a)
int dis[101],n,cost[101][101];
void dijkstra(int a)//模板
{
int vis[101],i;
for(i=0;i<n;i++)
{
dis[i]=max;
vis[i]=0;
}
dis[a]=0;
while(1)
{
int v=-1;
for(i=0;i<n;i++)
if(!vis[i]&&(v==-1||dis[i]<dis[v]))
v=i;
if(v==-1)
break;
vis[v]=1;
for(i=0;i<n;i++)
dis[i]=min(dis[i],dis[v]+cost[v][i]);
}
}
int main()
{
int m,j,i,a,b;
while(~scanf("%d%d",&n,&m))
{
for(i=0;i<n;i++)//初始化
for(j=0;j<n;j++)
cost[i][j]=max;
while(m--)
{
scanf("%d%d",&a,&b);
cost[a][b]=cost[b][a]=1;
}
int flag=1;
for(i=0;i<n;i++)
{
dijkstra(i);
for(j=0;j<n;j++)
{
if(dis[j]>7)
{
flag=0;
break;
}
}
if(flag==0)
break;
}
if(!flag)
printf("No\n");
else
printf("Yes\n");
}
return 0;
}
2、 SPFA:
#include<cstdio>
#include<queue>
#include<cstring>
#define INF 0x3f3f3f3f
using namespace std;
int head[205*2],num,n,dis[105],vis[105];
struct node
{
int from,to,val,next;
}A[205*2];
void chan(int a,int b)
{
node e={a,b,1,head[a]};
A[num]=e;
head[a]=num++;
}
int spfa(int sx)
{
memset(dis,INF,sizeof(dis));
memset(vis,0,sizeof(vis));
queue<int>q;
q.push(sx);
dis[sx]=0;
vis[sx]=1;
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=0;
for(int i=head[u];i!=-1;i=A[i].next)
{
int v=A[i].to;
if(dis[v]>dis[u]+A[i].val)
{
dis[v]=dis[u]+A[i].val;
if(!vis[v])
{
vis[v]=1;
q.push(v);
}
}
}
}
for(int i=0;i<n;i++)
if(dis[i]>7)
return 1;
return 0;
}
int main()
{
int m,a,b,i;
while(scanf("%d%d",&n,&m)!=EOF)
{
num=0;
memset(head,-1,sizeof(head));
while(m--)
{
scanf("%d%d",&a,&b);
chan(a,b);
chan(b,a);
}
for(i=0;i<n;i++)
{
if(spfa(i))
break;
}
if(i==n)
printf("Yes\n");
else
printf("No\n");
}
return 0;
}
3、 Floyd:
#include<cstdio>
#define INF 0x3f3f3f3f
int s[100][100];
int main()
{
int n,m,i,j,k,a,b;
while(~scanf("%d%d",&n,&m))
{
for(i=0;i<n;i++)
for(j=0;j<n;j++)
s[i][j]=INF;
while(m--)
{
scanf("%d%d",&a,&b);
s[a][b]=s[b][a]=1;
}
for(k=0;k<n;k++)
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(s[i][j]>s[i][k]+s[k][j])
s[i][j]=s[i][k]+s[k][j];
int flag=0;
for(i=0;i<n;i++)
for(j=i+1;j<n;j++)
if(s[i][j]>7)
{
flag=1;
break;
}
if(!flag)
printf("Yes\n");
else
printf("No\n");
}
return 0;
}
五、相关例题
以下题目适用于初学者,大牛们可跳过~~
HDU - 1385 Minimum Transport Cost
HDU - 3790最短路径问题
HDU - 2112 HDU Today
POJ 3259 -- Wormholes